大跨度板桁斜拉桥有限元建模方法

苏森林 张卓杰

华南理工大学，广州 510640

引言

板桁结构形式的桥梁整体性能好，同等跨度规模下，相对于混凝土桥重量轻、柔度大，抗风、抗震能力强，因而越来越广泛地应用于大跨度桥梁中，尤其是大跨度铁路桥和公铁两用桥中。如：芜湖长江大桥，天兴洲长江大桥，南京大胜关长江大桥，矮寨特大钢桁悬索桥等等，可见板桁结构被用于各式桥型当中。

1 板桁结构桥梁常见的建模方法

大跨度板桁斜拉桥总跨长一般达千米级，结构复杂，如此大规模的有限元模型中，单元动辄上万个，自由度数量更是翻倍。对于普通的计算机来说，如此庞大的计算量需要耗费大量的精力，而且如此高成本的计算在有些情况下不是必要的。所以，采用合适的有限元模型对大跨度板桁斜拉桥进行有效的模拟是有必要的。常见的空间有限元法将桁架杆件作为空间梁单元模拟，把桥面板作为空间板单元，而对纵横肋一般采用梁单元并划归到桥面板上，由此形成板梁混合单元。对此，国内外许多专家学者做过许多有意义的工作，如：日本学者伊藤学，小西一郎提出了正交异性钢桥面板的近似计算方法；大桥局桥科院采用平面杆系有限元分析方法，将混凝土桥面板按有效宽度折算为弦杆的一部分，或将混凝土板单元换算成独立的平面单元，将其与弦杆用刚性连接约束；同济大学滕小竹将板桁结构的主桁与桥面系整体等效为一根主梁等。

在桥梁结构分析计算时，为便于分析和设计，通常将主梁的受力分为如下三个体系[1]：第一体系将桥面板作为主梁的上翼缘；第二体系为盖板、纵肋和横梁（肋）组成的桥面系，盖板作为纵肋和横梁（肋）的共同上翼缘，仅承受桥面荷载；第三体系为“盖板体系”，即仅盖板本身，而桥面板的应力则等于上述各体系求得的应力之和。

2 工程背景

本文以在建的安徽铜陵公铁两用斜拉桥为工程背景，大桥全长1920m，为双塔五跨钢桁梁斜拉桥，跨径布置为90m+240m+630m+240m+90m，主跨630m。钢桁主梁为板桁结合结构，N型桁架。主桁总宽度为34.2m，横向采用三片主桁布置，桁高15.5m，节间长度15m。上、下弦杆均采用箱形截面。主塔为菱形钢筋混凝土结构，塔高220m。斜拉索为扇形三索面布置，采用钢绞线斜拉索，斜拉索共228根。

铁路和公路桥面系均采用密横梁正交异性钢板桥面。在主桥钢桁梁结构受力较大的区域及边墩和辅助墩需要压重的部位，铁路桥面局部采用正交异性箱型钢桥面。在其它结构受力较小的区域，将钢箱底板及其加劲肋取消，仅在横梁处设置横梁下缘底板。主梁标准截面布置如图1。

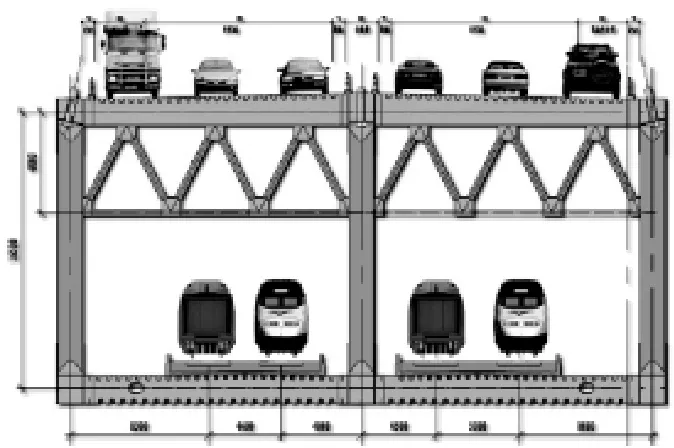
图1 主梁标准截面布置图（单位：mm）

3 大跨度板桁斜拉桥常用建模方法及其适用性

板桁组合结构主桁杆件、桥面系、纵梁、横梁、U肋等杆件都是由钢板焊成的，理论上讲，全桥整体分析中，这些构件全部可以采用板壳单元离散，但这样做计算自由度太多，计算时间长，数据整理工作量大，模型修改困难，所以全壳模型对于大跨度板桁桥来说并不适用。下面介绍几种常用的建模方法，并结合安徽铜陵长江大桥给出适用性上的说明。

3.1 空间板梁有限元模型（space plate-beam model，以下简称SPB模型）[2]

该法中主桁、纵横梁等杆件采用梁单元模拟，桥面板用空间板单元模拟，加劲肋采用梁单元模拟与桥面板共节点。这种方法的优点是能给较好地反映结构的实际情况，计算结果比较精确，但这种精确性是通过大量的板梁单元获得的。以铜陵长江大桥的SPB模型为例（见图2），全桥共216364个单元，其中228个索单元，105952个梁单元，110184个板单元，如此之多的单元数仍需要耗费大量的计算时间，故空间板梁法适用于设计的中后期，对桥梁施工过程和运营阶段的强度、刚度、稳定性等做全面的检算。

图2 SPB法模型局部示意图

3.2 改进的空间板梁法（modified space plate-beam model，以下简称M-SPB模型）

SPB模型中，加劲肋与桥面板单元共节点，加劲肋造成了桥面系节点数目剧增，本文特别提出改进的空间板梁法。该法依据正交异性板的等效原则，将加劲肋折算为板单元的厚度。等效的方法[4]：

(1) 桥面板的横向抗拉、压刚度按照EA等效；

(2) 板的面内面外抗弯刚度按照抗弯刚度等效；

(3) 板平面内的剪切刚度与实际结构等效。

由于该法用桥面板的等效厚度取代了原加劲肋，所以划分桥面板单元较SPB法有较大的随意性，所以该法大大节省了单元的数量同时保证了计算的精确度（见图3）。

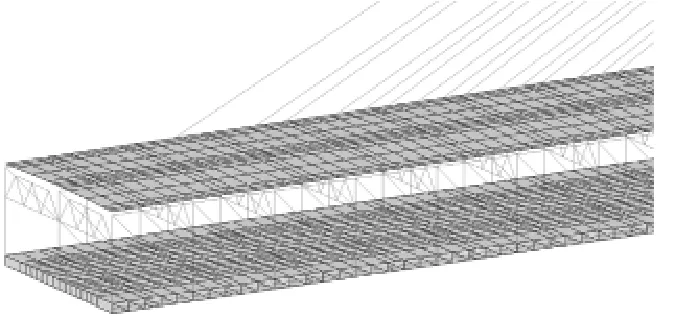
图3 M-SPB法有限元模型局部示意图

3.3 空间杆系结构法（space frame model，以下简称SF法）

该法的基本思想是将加劲肋直接按面积等效的原则折算到桥面板上，因为板桁组合结构的上弦杆在荷载作用下主要受拉或受压，作为上弦杆部分的桥面板也直接反应这一特征，文献[1]表明：结构的整体抗弯刚度由主桁桁高决定。桥面板板厚的小幅调整对结构的整体变形影响不明显，其影响仅表现在由于板厚的改变引起恒载变换所产生的结构变形。

再将桥面板按照一定的原则分割，等效到主桁弦杆，纵横梁上，全桥所有杆件均采用空间梁单元。求得的位移作为结构的实际位移，非桥面系杆件应力直接由SF模型给出，对于桥面系杆件的应力，必须要先确定桥面板的有效宽度，由SF模型中读取的内力换算出桥面系杆件的实际应力，文献[2]给出了桥面系板件有效宽度的计算方法。

SF法可以大大减少节点和单元数量，缩短计算时间，降低前后处理工作量。该方法适用于设计早、中期，主要是对主体结构进行优化，还可以用于施工过程的优化计算(见图4) 。

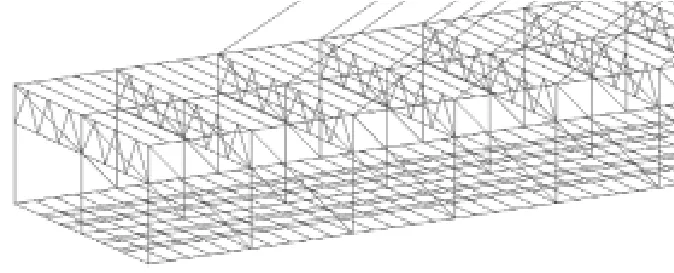
图4 SF法有限元模型局部示意图

4 计算结果

其具有更广泛的适用性。

以铜陵长江大桥为例，分别建立SPB模型，M-SPB模型，SF模型，各种模型所需单元类型及数量，桥面系单元所占单元总数百分比见表1所示。

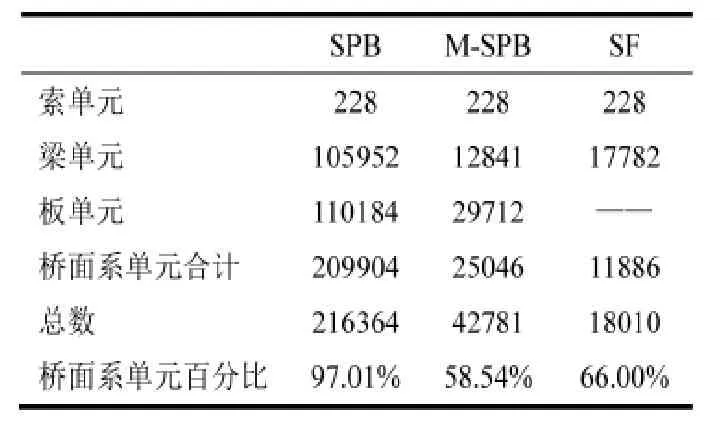
表1 三种方法建立全桥模型耗费单元数

分别用SPB法，M-SPB法，和SF法建立铜陵长江大桥一次成桥模型，拉索索力均以体内力的形式输入，通过迭代法不断调整拉索的初拉力或者调整无应力索长，使成桥索力与设计索力之差不大于1%，以此确定该桥的初始平衡状态[3]。对比三个模型的初始平衡状态的竖向位移，结果如下：

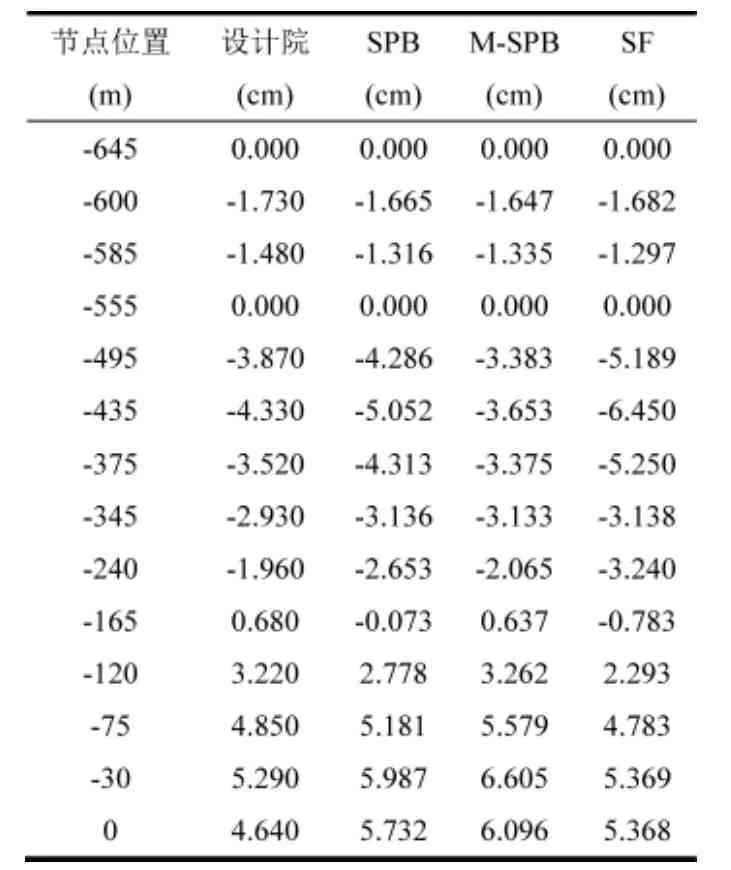
表2 三种模型的初始平衡状态竖向位移（半桥）

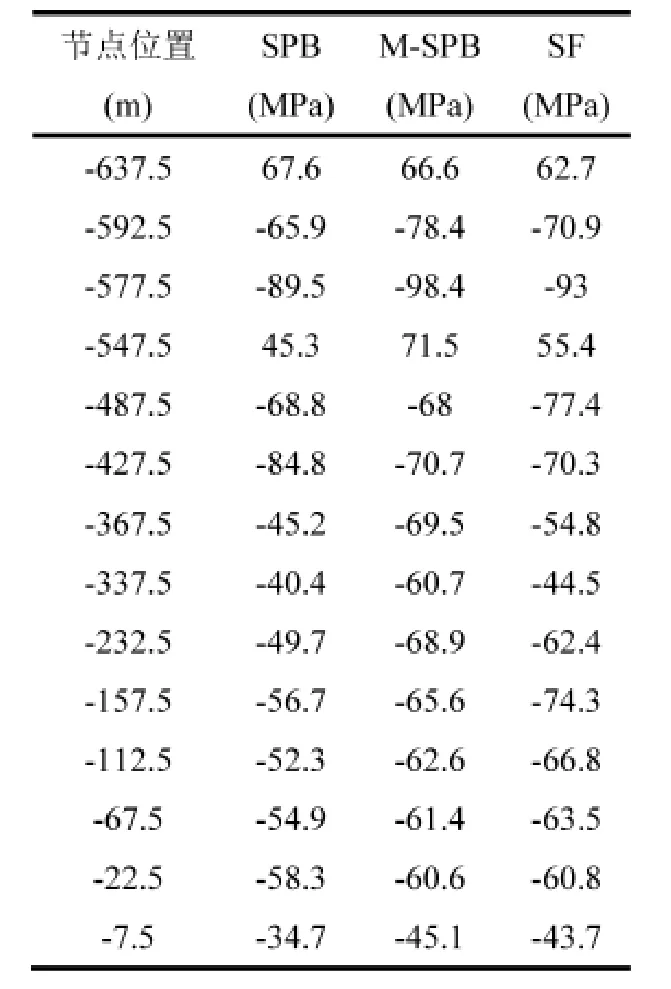
表3 中桁斜腹杆应力（半桥）

5 结语

（1）大跨度板桁斜拉桥结构复杂，构件数量多，为了提高分析效率，有限元模型可以根据实际需要进行不同深度的等效与简化，等效的基本原则是模型的刚度与质量分布与实际情况相符。

（2）由上述计算结果可见，三种模型计算出来的初始平衡状态的竖向位移很接近，与设计院给出的计算结果相比，最大相对误差不超过3cm，非桥面系杆件应力计算结果相近。对于本桥来说，满足计算精度要求，也验证了上述理论的正确性。

（3）SPB模型的计算精确度是基于精细的板梁单元模型，所以其计算效率差；SF法因为对板单元做了简化，计算高效率高，但这牺牲了桥面系板件应力的计算精度；M-SPB模型则介于SPB模型和SF模型之间，兼顾了计算精度和计算效率，可以作为结构设计中后期，施工控制的模型，可见

图5 初始平衡状态主梁挠度示意图

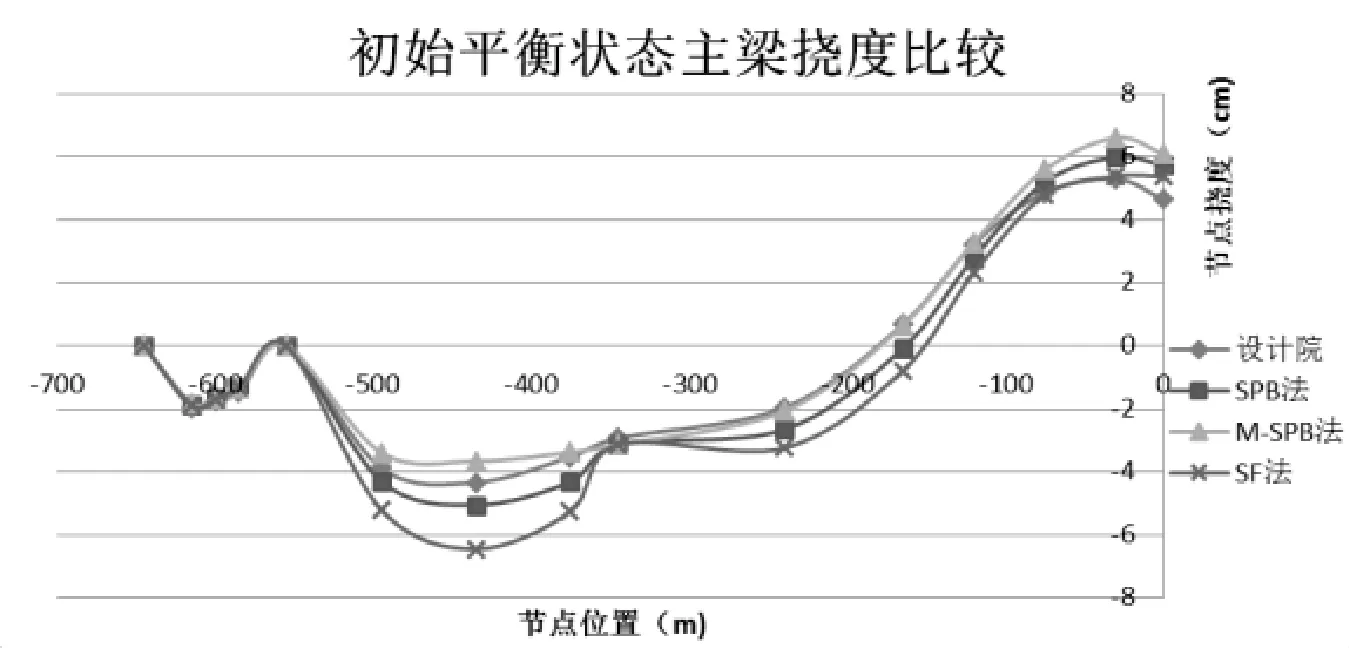
图6 三种模型的初始平衡状态竖向位移（半桥）

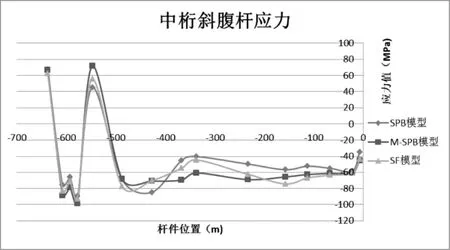
图7 三种模型的初始平衡状中桁斜腹杆应力（半桥）

[1]何畏，李乔.板桁组合结构体系受力特性及计算方法研究[J].中国铁道科学，2001，22(5)：65-72

[2]罗如登.高速铁路正交异性整体钢桥面结构形式受力性能和设计计算方法研究[D].中南大学，2010

[3]叶梅新，韩衍群，张敏.基于Ansys平台的斜拉桥调索方法研究[J].铁道学报，2006，28(4)：128-131

[4]赵金广，钱怡.基于Ansys参数化设计语言的正交各向异性钢箱梁结构优化设计.公路交通科技[J]，2008