环F2＋uF2＋…＋ukF2上的（1＋uk）－循环码

刘金秋， 刘 丽， 开晓山

（合肥工业大学 数学学院，安徽 合肥 230009）

环F2＋uF2＋…＋ukF2上的（1＋uk）－循环码

刘金秋， 刘 丽， 开晓山

（合肥工业大学 数学学院，安徽 合肥 230009）

文章确立了环F2＋uF2＋…＋ukF2上码长为奇数n的（1＋uk）－循环码的结构，给出自对偶码存在的充要条件，讨论了环F2＋uF2＋…＋ukF2上的（1＋uk）－循环码及其对偶码的Gray映射，并且得到它们之间的关系。

循环码；常循环码；Gray映射；自对偶码

随着近20a的发展，有限环上的编码理论获得重要突破，其理论研究得到了学者的广泛关注，而有限环上常循环码（包括循环码和负循环码）以及自对偶码是有限环上纠错码研究的热点。

文献［1］讨论了环Z4上的循环自对偶码；文献［2］将文献［1］进行了推广，得到了Zpm上循环码的结构；文献［3］研究了Z4上的循环码和负循环码；文献［4］完全地给出了一般有限链环上单根循环码和负循环码的结构，这实际上也分类了有限链环上所有单根常循环码；文献［5］研究了环Fq＋uFq＋…＋us－1Fq上的常循环码；文献［6］研究了环F2＋uF2＋u2F2＋…＋umF2上的（1－um）－循环码，亦得到了一些较好的性质。此后，分类有限链环上任意长度的常循环码成为有限环上编码理论研究的一个重点，同时也是一个难点，环上编码理论研究进入了相对比较缓慢的阶段。文献［7－8］分别给出了环F2＋uF2和环F2＋uF2＋u2F2上的循环码和常循环码的结构。

近几年，码的Gray像也得到了广泛研究，文献［9－10］给出了Gray像的一些性质，这些研究成果在很大程度上丰富了有限环上的编码理论，也拓展了研究方向。

本文在已有研究结果的基础上进一步展开对常循环码的研究，给出了环F2＋uF2＋u2F2＋…＋ukF2上长为n（n为奇数）的（1＋uk）－循环码及其对偶码的结构，并对其Gray像进行了研究，对全面认识常循环码及构造一些高效、纠错性能好的码都具有一定的意义。

1 预备知识

记R＝F2＋uF2＋…＋ukF2，该环中任一元素可记为a＝a0＋a1u＋…＋akuk，ai∈F2。

R是一个局部环，它的极大理想为（u）。R的理想构成一个链（0）⊂（uk）⊂…⊂（u2）⊂（u）⊂（1）＝R，其中u为幂零元，u的幂零指数为k＋1。则1＋uk∈R且满足1＋uk≡／0（modu），故1＋uk为R中的单位。

码字c＝（c0，c1，…，cn－1）∈C的多项式，表示为c（x）＝c0＋c1x＋…＋cn－1xn－1∈R［x］。

2 R上（1＋uk）－循环码的结构

设V为上的同构映射（a0，a1，…，an－1）＝ （（1＋uk）an－1，a0，a1，…，an－2），若（C）＝C，则称C是R上长为n的（1＋uk）－循环码。

定理1 设n为奇数，xn－（1＋uk）＝f1f2…fr，其中fi∈R［x］，1≤i≤r为两两互素的基本不可约多项式。则Rn＝R［x］／（xn－（1＋uk））的理想是一些 （＋ （xn－ （1＋uk））），（＋ （xn－（1＋uk））），（u＋（xn－（1＋uk））），…，（＋（xn－（1＋uk）））的直和，其中0≤i≤r，＝（xn－

证明 由于f1，f2，…，fk＋1两两互素，故

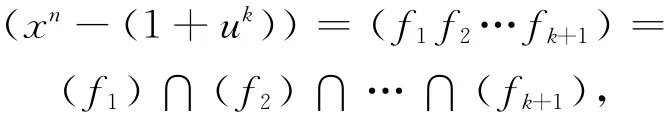
由中国剩余定理，知

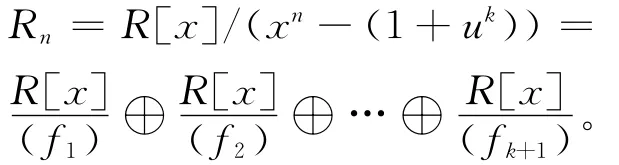
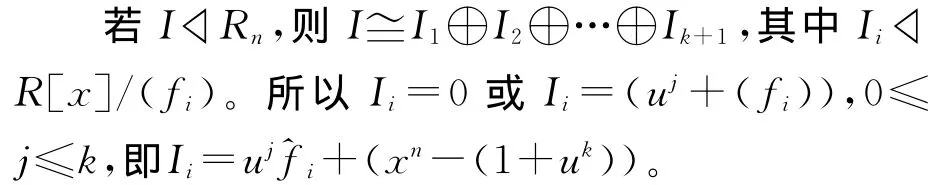
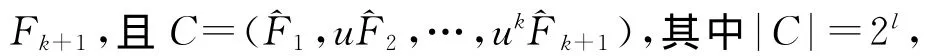
证明 设xn－（1＋uk）＝f1f2…fr，其中fi∈R［x］，0≤i≤r是两两互素的基本不可约多项式。由定理1，C是一些（）的直和，不妨设C是下列形式的直和：

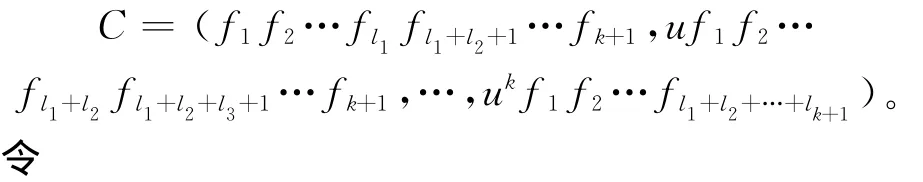
3 R上（1＋uk）－循环码及其对偶码

引理1 设C是R上长为n的（1＋uk）－循环码，其中n为奇数，｜C｜＝2l，｜C⊥｜＝2h，则｜C｜｜C⊥｜＝2（k＋1）n，即h＋l＝n（k＋1）。

定理3 设C是长度为n的R上的（1＋uk）－循环码，且C＝（，，…，），其中xn－（1＋uk）＝F0F1…Fk＋1，且F0，F1，F2，…，Fk＋1彼此互素（可以为1），则C⊥＝，，，…），｜C⊥｜＝2h，这里h＝Fi＋1，其中F＊＝（1／x）是F的互反多项式。

证明 令C1＝（，，，…，），下证C1＝C⊥。对0≤i，j≤k，若i＋1≠（k＋1）－j＋1，则

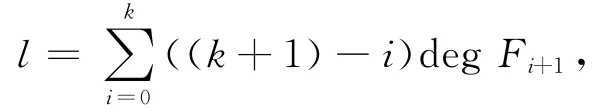
又由 引 理 1 知h1＋l＝n（k＋1），故h1＝Fi＋1＝h，即｜C⊥｜＝｜C1｜，故C1＝C⊥。

命 题 1 设C＝，…，），且F0F1…Fk＋1＝xn－（1＋uk），则C是自对偶码⇔对所有i，j∈｛0，1，…，k＋1｝，i＋j≡1（mod（k＋2））都有Fi与相伴。

证明 ⇐由定理3得C⊥＝（，，，…，）。若对所有的i，j∈｛0，1，…，k＋1｝，使得i＋j≡1（mod（k＋2））都有Fi与相伴，则有：

即C是自对偶码。

⇒假设C＝C⊥，且ci为Fi的常数项，0≤i≤k＋1。因为

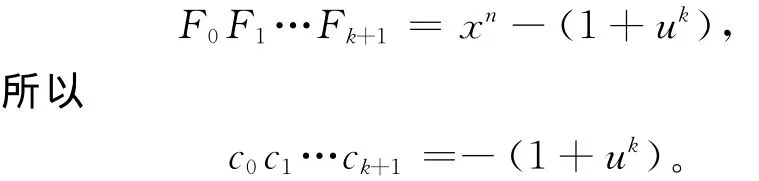
故ci是R中的可逆元且是的首项系数。对∀i，j∈｛0，1，…，k＋1｝，使i＋j≡1（mod（k＋2）），记Gi＝，其中ui是R中的可逆元，使Gi为首一多项式，则ui＝，且

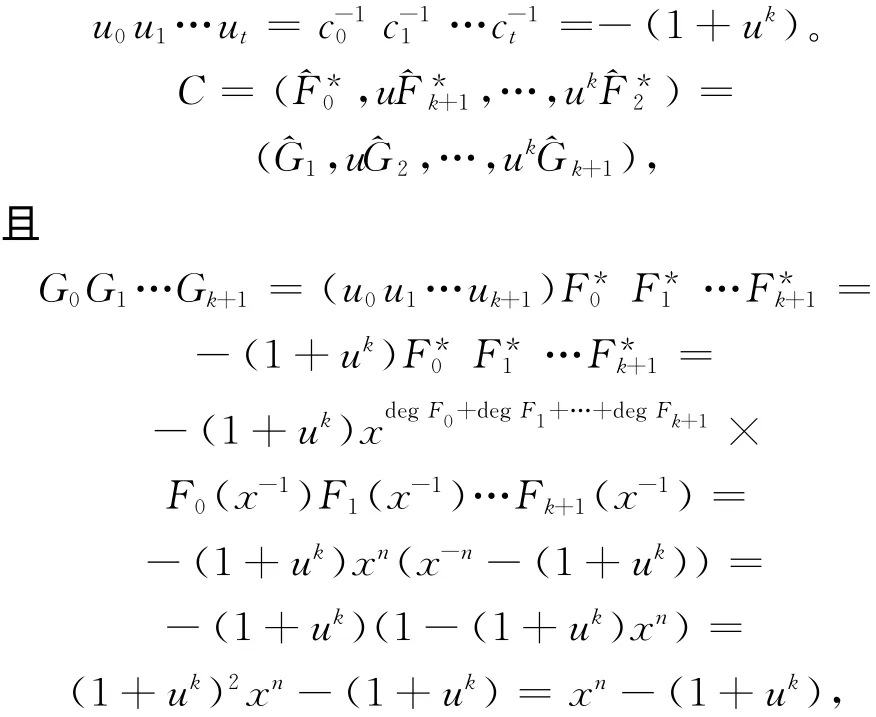
则Fi＝Gi＝。

定理4 假设k为奇数，则非平凡自对偶（1＋uk）－循环码存在⇔R［x］中存在xn－（1＋uk）的一个基本不可约因式f，使得f与f＊不相伴。

证明 ⇒假设存在一个非平凡自对偶（1＋uk）－循环码C＝（，，…，），其中F0，F1，…，Fk＋1∈R［x］为首一多项式，且满足F0F1…Fk＋1＝xn－（1＋uk）。假设xn－（1＋uk）的所有基本不可约因式f都与f＊相伴，则i＝0，1，…，k＋1时，Fi与也相伴。

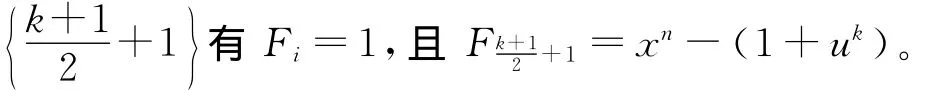
故C＝）是平凡自对偶码，与条件矛盾。即证存在f，使得f与f＊不相伴。

⇐假设R［x］中存在xn－（1＋uk）的一个基本不可约因式f，使f与f＊不相伴，则f的常数项非零，degf＝degf＊，f＊｜xn－（1＋uk），故ff＊｜xn－（1＋uk）。则存在g∈R［x］，使xn－（1＋uk）＝ff＊g。

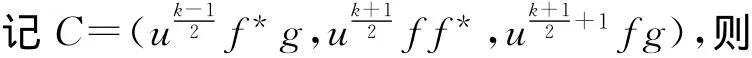
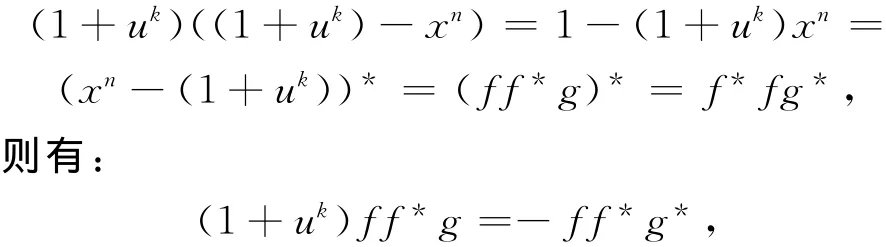
即g＊＝－（1＋uk）g。由定理3，得

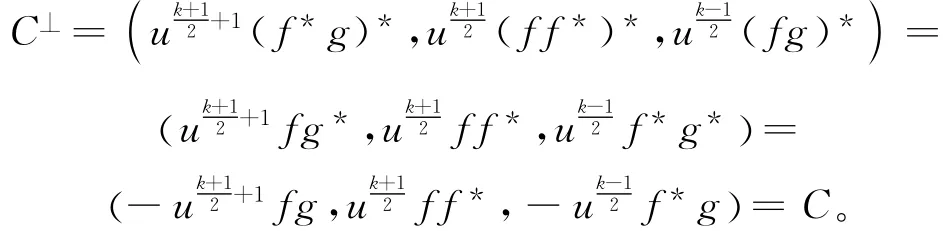
定理5 假设R是有限链环，其极大理想为（u），uk＋1＝0。若k＋1为偶数，则R上长为奇数n的非平凡自对偶（1＋uk）－循环码存在⇔对所有i都有2i≡／－1（modn）。

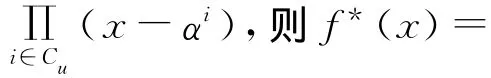
推论1 若n是一个奇素数，则当n≡±3（mod 8）时，R上 不 存 在 长 为n的 自 对 偶（1＋uk）－循环码。

定理6 设C是R上长为n的（1＋uk）－循环码，则C⊥也是（1＋uk）－循环码。

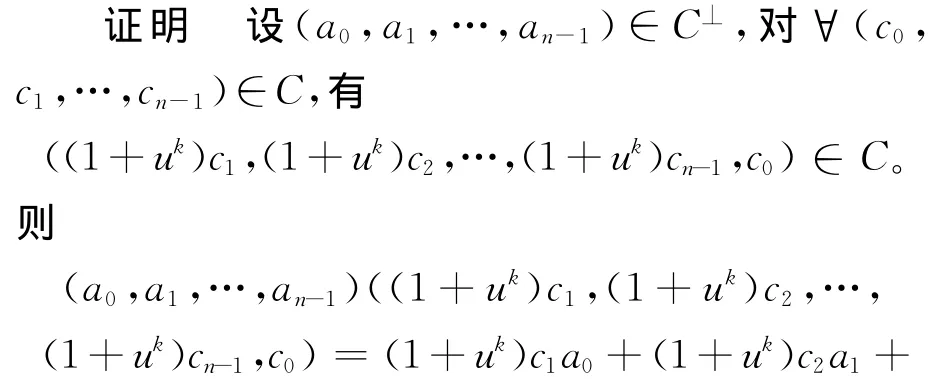
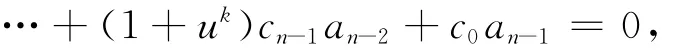
等式两边同乘以1＋uk，得

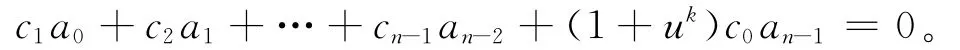
所以（（1＋uk）an－1，a0，a1，…，an－2）∈C⊥，故C⊥是（1＋uk）－循环码。

4 R上（1＋uk）－循环码及其Gray映射

对任意x∈R，都可唯一表示成x＝r0（x）＋ur1（x）＋…＋ukrk（x），其中ri（x）∈F2，i＝0，1，…，k。为防止混淆，用“＋”表示环R中的加法运算，域F2中的运算用“⊕”表示。

令A＝ （A0，A1，…，An－1）∈Rn，ri（A）＝（ri（A0），ri（A1），…，ri（An－1）），i＝0，1，…，k。设z是任意正整数，则z＝p0（z）＋2p1（z）＋22p2（z）＋…，0≤pi（z）≤1，i＝0，1，2，…。

设s、m为任意正整数，令

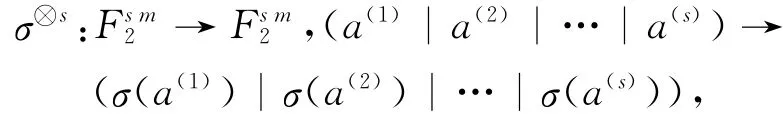
其中，a（1），a（2），…，a（s）∈，σ为上 的 循 环 移位，则σ⊗s表示指数为s的准循环移位变换。

域F2上满足σ⊗s（c）＝c的码c称为长sm指数为s的准循环码。

定义1 设映射Φ为：

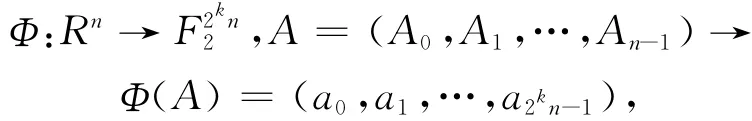
其中，当k≥2时，则

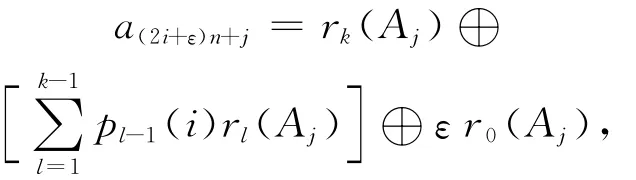
当k＝1时，则

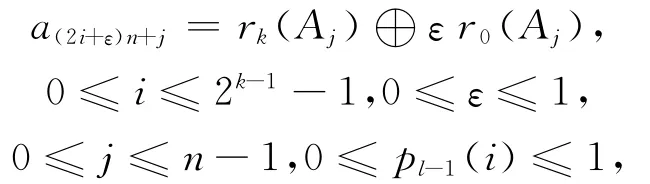
则称Φ为Rn→的Gray映射。

定理7 若C是长为奇数n的R上的自对偶（1＋uk）－循环码，则Φ（C）是长为2kn的上的自正交码。

证明 ∀A＝（A0，A1，…，An－1），B＝（B0，B1，…，Bn－1）∈C，其中Ai，Bi∈R，则由C是Rn上的自对偶码得AB＝0。即有：

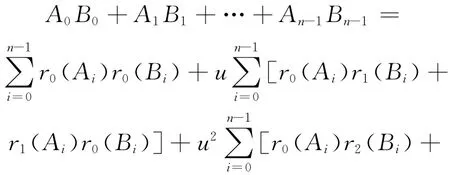
例1 若C是长为奇数n的F2＋uF2＋u2F2上的自对偶（1＋u2）－循环码，则Φ（C）是长为4n的上的自正交码。

证明 记Φ（A）的对偶码为（Φ（A））⊥，∀A＝（A0，A1，…，An－1），A′＝（A0′，A1′，…，An－1′）∈C，其 中Ai＝ai＋ubi＋u2ci，Ai′＝ai′＋ubi′＋u2ci′。由C是F2＋uF2＋u2F2上的自对偶码得AA′＝0。即有：

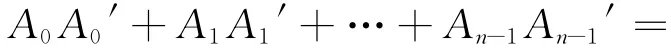
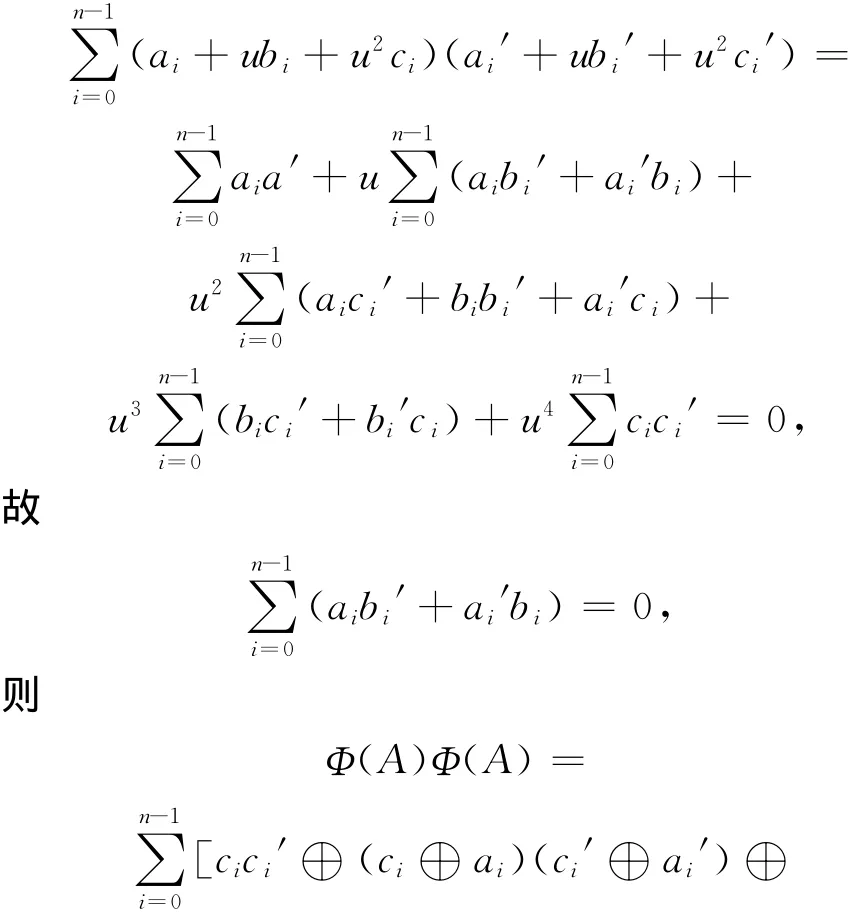
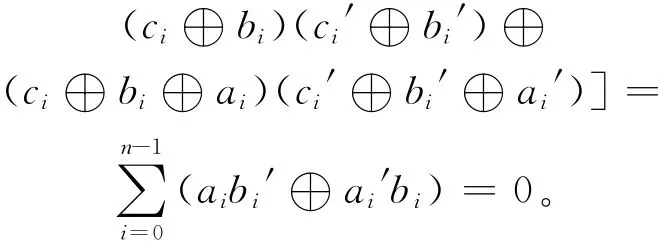
所以Φ（A′）⊆（Φ（A））⊥，得证。

性质1 令λ＝1＋uk∈R，有ΦVλ＝。

定理8 环R上长为n的码C是（1＋uk）－循环码的充要条件，是其Gray像Φ（C）是域F2上长为2kn、指数为2k－1的准循环码。

［1］Pless V，Sol P，Qian Z.Cyclic self－dualZ4－codes［J］.Finite Fields Appl，1997（3）：48－69.

［2］Kanwar P，López－Permouth S R.Cyclic codes over the integers modulopm［J］.Finite Fields Appl，1997（3）：334－352.

［3］Wolfmann J.Negacyclic and cyclic codes overZ4［J］.IEEE Trans Inform Theory，1999（45）：2527－2532.

［4］Dinh H.Q，López－Permouth S R.Cyclic and negacyclic codes over finite chain rings［J］.IEEE Trans Inform Theory，2004（8）：1728－1744.

［5］Zhu S X，Shi M J.Constacyclic codes over ringFq＋uFq＋…＋us－1Fq［J］.Journal of University of Science and Technology of China，2009，39（6）：583－587.

［6］Cengellenmis Y.On（1－um）－cyclic codes overF2＋uF2＋u2F2＋u3F2＋…＋umF2［J］.Int J Contemp Math Sciences，2009，20（4）：987－992.

［7］Qian J F，Zhang L N，Zhu S X.（1＋u）－constacyclic and cyclic codes overF2＋uF2［J］.Applied Mathematics Letters，2006（19）：820－823.

［8］Qian J F，Zhang L N，Zhu S X.Constacyclic and cyclic codes overF2＋uF2＋u2F2［J］.IEICE Trans Fundamentals，2006（6）：1863－1865.

［9］朱士信，吴 波.环Fp＋uFp＋…＋ukFp上的线性码和常循环码的Gray像［J］.合肥工业大学学报：自然科学版，2006，29（8）：1049－1052.

［10］王 玉.环F2＋uF2＋…＋ukF2上的循环码和（1＋uk）循环码［J］.合肥工业大学学报：自然科学版，2009，32（7）：1117－1120.

（1＋uk）－cyclic codes over the ringF2＋uF2＋…＋ukF2

LIU Jin－qiu， LIU Li， KAI Xiao－shan
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

The structure of（1＋uk）－cyclic codes of odd lengthnover the ringF2＋uF2＋…＋ukF2is established.And the necessary conditions for the existence of self－dual codes are given.Finally，the Gray images of（1＋uk）－cyclic codes and its dual codes are studied respectively，and their relationship is given.

cyclic code；constacyclic code；Gary mapping；self－dual code

TN911.22

A

1003－5060（2013）01－0124－05

10.3969／j.issn.1003－5060.2013.01.026

2012－07－16

安徽省高等学校省级自然科学研究重点资助项目（KJ2009A44）

刘金秋（1988－），女，安徽淮北人，合肥工业大学硕士生；

刘 丽（1965－），女，安徽枞阳人，博士，合肥工业大学教授，硕士生导师.

（责任编辑 吕 杰）