PI adaptive control based on partition of unity for a class of uncertain nonlinear systems
LUO Liang,GUO Shu-min,SONG Jie
(College of Mathematics and Information Science,Shaoguan University,Shaoguan 512005,Guangdong,China)
The adaptive control of uncertain nonlinear systems has received increasing attention and many significant developments have been achieved in field of control theory and applications.It is noted that adaptive control is one of important methods in the existing methods for dealing with uncertainty[1].Adaptive control schemes reduce uncertainties by learning them.The objective,in adaptive control,is to introduce an adaptive law for adjusting the parameters of the controller or the system against system uncertainties and disturbances.Generally speaking,the designing process is composed of two main steps.First,the uncertainties are parameterized by employing certain types of function approximators such as spline function approximators[2-3],fuzzy function approximators[4-5],and neural network base function approximators[6-7],and so on.Then the adaptive laws are constructed for estimating and adjusting the parameters,and the controller is constructed by using estimate values of the parameters.However,such methods generally guarantee parameter convergence only if parameter changes are slow enough[8].
Fuzzy logic control,as an alternative to conventional control methodologies handing uncertainty,has been the focus of numerous studies in the past two decades[9-10].Fuzzy modeling formulates the system knowledge with rules in a transparent way to interpretation and analysis(to a certain degree)so as to gain insights into the system being modeled.This has opened up a brand-new approach to modeling complex systems in system identification and control,fault diagnosis,classification and intelligent data analysis,etc.For example,an adaptive fuzzy logic control scheme was developed in for a class of nonlinear systems[9].It includes an adaptive law for the fuzzy controller’s parameters and a PI-adaptive fuzzy controller to provide added robustness in the presence of bounded uncertainties and external disturbances.The above fuzzy control scheme can ensure that the all states of the closed-loop systems to be stabilized and parameters to be bounded.Based on this work,more research has been done[10].These methods in[10]demand a common theoretical basis,namely PI type switching structure that provides a mechanism to cope with the bounded large-and-fast disturbance with unknown bound while the typical chattering of the switching law is significantly attenuated.However,the previous results are obtained mainly by utilizing the grid-partition to generate input space.
Note that the high-level interpretability refers to fuzzy model interpretability obtained by increasing the number of fuzzy rules.Fuzzy rules can be generated based on human expert knowledge or heuristics,which offers a good high-level semantic generalization capability.However,for complex systems,the interactions between system behaviors are very difficult to be grasped so that the system model just based on expert knowledge may suffer from a loss of accuracy and combinatorial rule explosion.It is clearly that the more to increase total number of the fuzzy rules,the easier to create the curse of dimensionality.The curse of dimensionality is a significant obstacle to solving machine learning problems that involve learning a “state-of-nature’’ from a finite number of data samples in a high-dimensional space.One efficient way of evading this problem for fuzzy systems is to generate the input space via scatter-partition(prototype)rather than grid-partition[11].
The partition of unity,which is a concept in differential geometry,was one of methods based on the scatter-partition.With the aid of this concept,we can first locally decompose the system state space.Then we put together the local properties exhibited in the subspaces,thus obtain some certain integral properties of the system.The partition of unity method has proved to be an effective mean in material and rock mechanics which have obtained such achievements as improved finite element computation algorithms by using partition of unity[12-13].Yet these methods do not relate to control design problems.In terms of system design,the linear combinations of partition of unity have been proved to have the ability to approximate continuous functions at arbitrary precision on a compact region of Euclid space[14].Robust controllers have been designed for some uncertain linear systems by using this ability to approximate the uncertainties of the systems together with Lyapunov method[14-18].In connection with the papers,it is shown that the basis functions of partition of unity can flexibly selected to approximate nonlinear and uncertainties.On the other hand,the control algorithm takes the advantages of systematic design in partition of unity while effectively circumvent the curse of dimensionality.
Inspired by the works of[9-10],we propose a new control architecture.We adopt the partition of unity concept to design an adaptive strategy that contains the PI adaptive robust control structure for a class of uncertain nonlinear systems with large and fast disturbance rejection.It has been proves that this control scheme with PI adaptive structure can guarantee the closed-loop system asymptotic stability and the tracking error converges asymptotically to zero.
This paper is organized as follow.In section 2,we present a brief description of the basic concept and the approximation lemmas.In section 3,we design and prove stable control schemes based on Lyapunov synthesis approach.In section 4 the new control architecture is used to control an inverted pendulum system.To demonstrate the effectiveness of the proposed method,system performance is compared with approach[10].Finally,section5 concludes the main advantages of the proposed method in this paper.
1 Preliminaries and Approximation Lemmas


2 Control design for uncertain nonlinear systems based on ESPU-



Remark 5(1)the states and parameters of the closed-loop systems can be stabilized in the meaning of UUB via the robust nonlinear controller and adaptive laws.(2)In this paper,partition of unity is used in the adaptive controller to circumvent the curse of dimensionality encountered in the implementation of the fuzzy logic controller.Because that the partition of unity is not based on grid-partition in paper[14-18],it has the property of scatter-partition for flexibility in the selection of coverage of the domain.So it may be employed to deal with many diverse applications.
3 Simulation example
In this section,we mainly apply the control schemes developed in this paper to control an inverted pendulum system under very fast and large disturbances.
Consider the following a second-order model of the inverted pendulum system:

The initial conditions of partition of unity parameters are chosen randomly in the intervals [0,1].The partition of unity{αk}subordinating to the sphere regions can be chosen by using the method introduced in[14].
We choose the disturbance(d(t)=4cos(50πt)).Fig 1 shows the error signal of the referenced adaptive fuzzy controller in [10].Obviously,from the Fig 1,we can not see differences between POU(partition of unity)method and FLS (fuzzy logical system)method in [10].Under the local amplification of Fig 2,in the time region of t=6.5 to 8,we find that the tracking error of POU method is not only smaller but also faster to zero than the FLS method in [10].
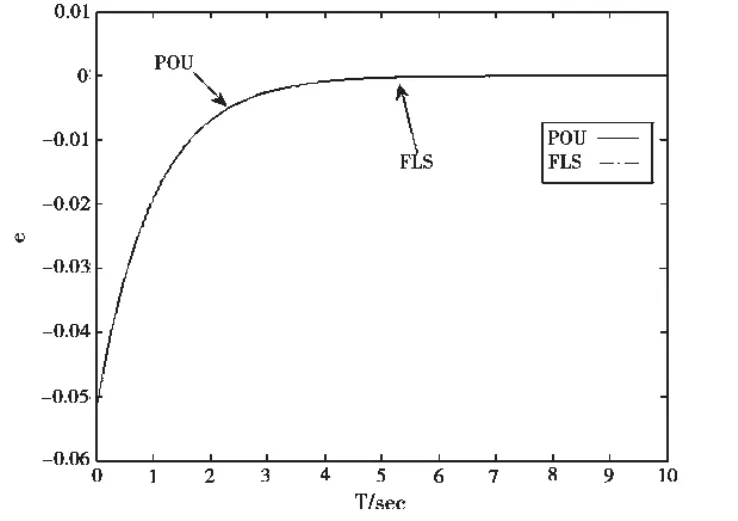
Fig1 The tracking error of state x1(d(t)=4cos(50πt))
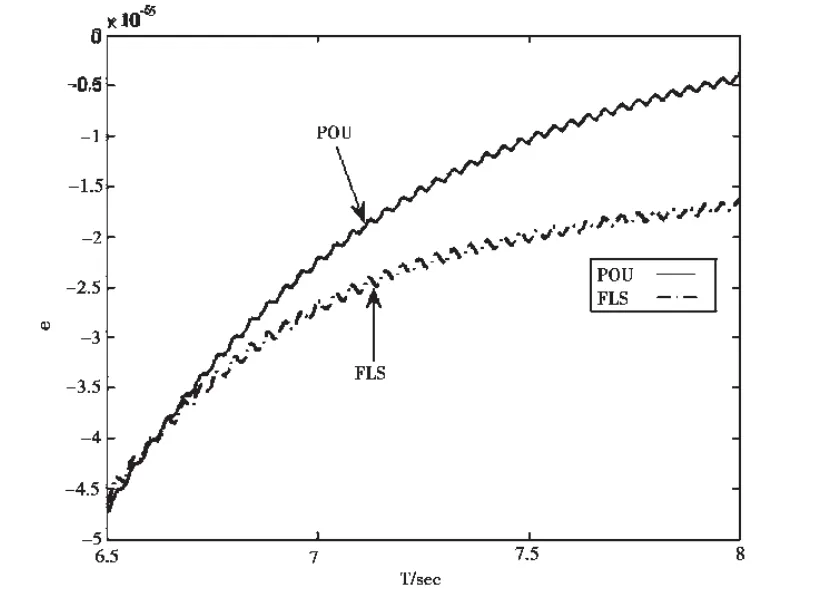
Figt2 The local enlarge segment of Fig 1(d(t)=4cos(50πt))
Consider the other very larger disturbance(d(t)=10cos(50πt)).According to paper[4],we increase the original amplitude of disturbance to(d(t)=10cos(50πt)),the corresponding simulation is displayed in Fig 3.Based on Fig 4,we can also be observed that the proposed POU controller achieves a significantly better tracking performance than FLS controller during the time region of t=3.5 to 6.

Fig3 The tracking error of state x1 (d(t)=10cos(50πt))

Fig4 The local enlarge segment of Fig 3 (d(t)=10cos(50πt))
4 Conclusion
The partition of unity method is used in this paper to decompose the compact set of state space of the controlled system into certain open covering.The linear combination of certain partition of unity subordinate to certain open covering possesses the capability of approximating continuous functions or arbitrary precision.In this paper,we compared the work of an earlier reference by proposing a PI adaptive partition of unity controller that bound dose not need to be known and uncertainties can be fast.In order to test the performance of the proposed algorithm,it is applied to a nonlinear model of an inverted pendulum amid larger system disturbances.Results in this paper indicate that we can use proper open covering and the proportionalintegral(PI)error feed-back structure to cope with the chatting while maintaining asymptotic convergence under larger and fast disturbance.The method in this paper is based on partition of unity,which is not based on grid-partition,this may circumvent the curse of dimensionality encountered in the implementation of the fuzzy logic controller.
[1]Khalil H K.Nonlinear Systems[M].2nd ed.NJ:Prentice-Hall,1996.
[2]Mutnury B,Swaminathan M,Libous J.Macro-modeling of non-linear I/O drivers using spline functions and finite time difference approximation[C]//Electrical Performace of Eletronic Packaging,Princeton,NJ:IEEE Society,2003:273-276.
[3]Cruz-Roldan F,Martin-Martin P,Saez-Landete,et al.A Fast Windowing-Based Technique Exploiting Spline Functions for Designing Modulated Filter Banks[J].Circuits and Systems I:Regular Papers,IEEE Transactions on,2009,56(1):168-178.
[4]Kazuo Tanaka,Takayuki Ikeda,Wang Hua O.Robust Stabilization of a Class of Uncertain Nonlinear Systems via Fuzzy Control:Quadratic Stabilizability,Control Theory,and Linear Matrix Inequalities[J].Fuzzy Systems,IEEE Transactions on,1996,4(1):1-13.
[5]Bai Shi Zhen,Zhang Song Tao.Robust Fuzzy Control of Uncertain Nonlinear Systems Based on Linear Matrix Inequalities[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation:WCICA 2008,Chongqing:IEEE Society,2008:25-27.
[6]Zuo Wei,Cai Li-long.Adaptive Fourier Neural Network Based Control a Class of Uncertain Nonlinear Systems[J].Neural Network,IEEE Transactions on,2008,19(10):1689-1701.
[7]Yoo Sung Jin,Park Jin Bae,Choi Yoon Ho.Adaptive Neural Control for a Class of Strict-Feedback Nonlinear Systems with State Time Delays[J].Neural Network,IEEE Transactions on,2009,20(7):1209-1215.
[8]Astrom H J,Wittenmark B.Adaptive Control[M].2nd ed.New York:Addison-Wesley,1994.
[9]Shahnazi R,Akbarzadeh-T M R.Robust PI adaptive fuzzy control for a class of uncertain nonlinear systems[C]//IEEE International Conference Systems,Man,Cybernetics:SMC 2005,Hawaii:IEEE Society,2005,3:2566-2571.
[10]Shahnazi R,Akbarzadeh-T M R.Robust PI adaptive fuzzy control with large and fast disturbance rejection for a class of uncertain nonlinear systems[J].Fuzzy Systems,IEEE Transactions on,2008,16(1):187-197.
[11]Zhou S M,Gan John Q.Low-level interpretability and high-level interpretability:a unified view of data-driven interpretable fuzzy system modeling[J].Fuzzy Sets and Systems,2008(159):3091-3131.
[12]Bacciotti A.Further remark on potentially global stable[J].Automation Control,IEEE Transactions on,1989,34(6):637-638.
[13]Melenk J M,Babuska I.The partition of unity finite element method:basic theory and applications[J].Computer Methods in Applied Mechanics and Engineering,1996,139(3):289-314.
[14]Wang Y H,Li Z Y,Zhang S Y.Approximation property of partition of unity and its applications [J].Journal of Control Theory and Applications,2004,2(3):267-275.
[15]Wang Y H,Li Z Y,Zhang S Y.Universal approximator and control design based on partition of unity[J].Circuits and Systems,WSEAS Transactions on,2004,3(8):1676-1681.
[16]王银河,韩东方.基于单位分解的一类非线性系统的变结构控制设计[J].控制与决策,2006,21(8):853-856.
[17]Wang Y H,Han D F.Guaranteed Cost Control for a Class of Nonlinear systems based on partition of unity[C]//Proceedings of the 6th World Congress on Intelligent Control and Automation:WCICA 2006,Dalian:IEEE Society,2006:21-23.
[18]Han D F,Wang Y H,Zhang SY.Control synthesis for a class of nonlinear systems based on partition of unity [J].Journal of Control Theory and Applications,2007,5(21):145-151.
[19]Boothby W M.An introduction to differentiable geometry[M].2nd ed.New York:Academic Press,INC,1986.
[20]Slotine J J,Li W.Applied Nonlinear Control[M].Englewood Cliffs:Prentice-Hall,1991.

