突变理论在煤层气储层评价中的应用——以准噶尔盆地砂沟井田为例

孙文卿 冉茂云 熊建龙 张军 赵文峰 刘文辉

四川省煤田地质工程勘察设计研究院

煤层气储层评价是煤层气资源勘探开发的基础和依据。前人针对煤层气储层评价采用了较多的方法，如模糊综合评判法[1]、灰色关联法[2]、神经网络法[3]、聚类分析法[4]、层次分析法[5]等，对煤层气储层评价起到了积极作用。笔者以新疆准南煤田砂沟井田为例子，综合考虑煤层气资源特征、开采性能、煤层特征、构造特征等因素，构建了砂沟井田煤层气储层评价体系，基于突变理论对井田煤层气储层进行了评价，为煤层气储层评价提供了一种方法。

1 突变评价原理及评价方法

1.1 突变评价原理

突变理论是法国数学家Rene.Thom创立的一门综合利用拓扑学、奇点理论和结构稳定性研究非连续变化和突变现象的数学学科[6]，特别适用于内部作用尚未确知系统的研究[7]，也可进行多目标对象排序优选[8]。在工程技术、安全科学、经济管理、社会科学等众多领域得到广泛应用[9－11]。

常见的突变类型有3类，即尖点突变模型、燕尾突变模型、蝴蝶突变模型[6]，其势函数[V（x）]及突变系统的分歧点集（B）方程见表1。当控制变量（t、u、v、w）满足分歧点集方程时，系统就会发生突变。以尖点突变模型为例，如图1，当势函数的指点处于折痕线上（即u、v满足分歧点集方程），势函数值从上叶越过中叶直接突跳到下叶，或者从下叶越过中叶直接突跳到上叶，即系统发生突变。

表1 常见突变类型及其势函数方程表

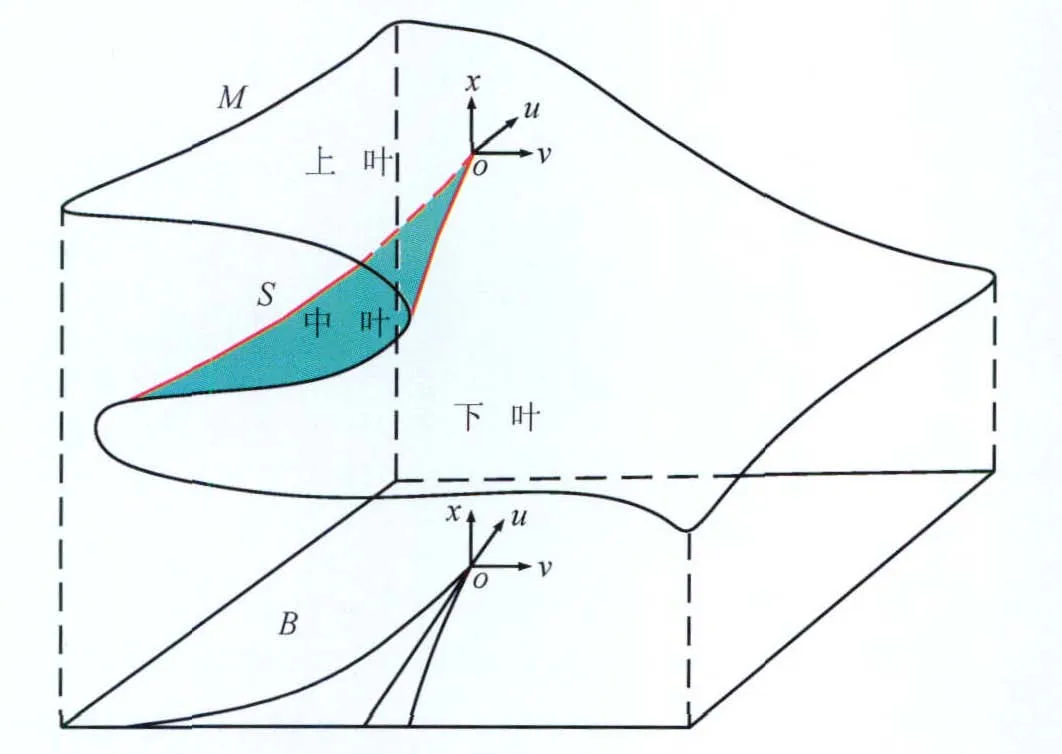
图1 尖点突变模型图

1.2 突变隶属函数值计算

通过分解形式的分歧方程可导出归一公式，运用归一公式可求出系统总突变隶属函数值。常用的3种突变模型的归一公式如下：

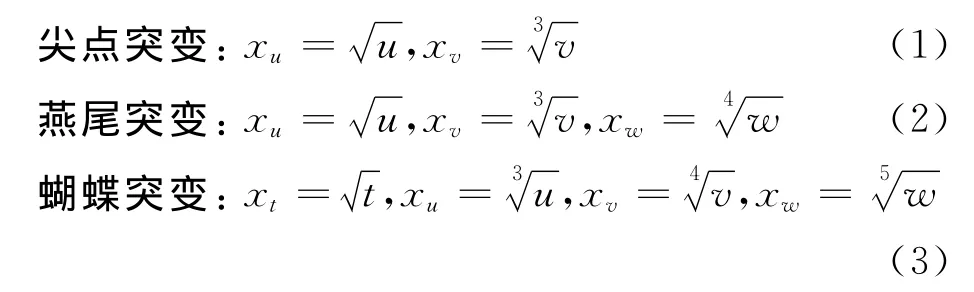
在归一公式中状态变量及诸控制变量均取0～1范围的数值。

1.3 评价方法

首先将评价系统分解为由若干评价指标组成的多层子系统，进而构建突变评价评价指标体系；然后对指标控制变量进行无量纲化，运用数学方法产生一种多维的突变模糊隶属度值（在0～1间取值，值越大代表越优）；利用归一公式对同一系统各控制变量计算出相应的x值，进而求出不同评价系统的总突变隶属度值；最后根据隶属函数值的大小排序，进行不同评价系统评价。

2 煤层气储层评价模型建立及应用

砂沟井田位于准噶尔盆地南缘，乌鲁木齐山前坳陷东段阜康凹陷东部黄山街倒转向斜的北翼，为一向南倾的单斜构造，煤系地层形态总体为一近东西走向、倾向南的单斜构造。井田一带煤层均赋存于下侏罗统八道湾组（J1b）中，编号煤层21层。其中的 M5、M6、M8、M9、M19号煤层为井田一带的主要煤层，煤层厚度大、含气量高，为井田煤层气勘探开发提供了条件。

2.1 评价体系建立

综合考虑，将砂沟井田富集高产的有关因素分为资源特征、开采性能、煤层特征和构造特征4种类型，根据层次分析法的基本原理[12]，建立由目标层、准则层和指标层组成的煤层气储层评价指标结构层次（图2），运用各指标间的相互关系确定指标间的重要性排序，并确定突变模型（图3）。砂沟井田目标煤层评价指标值见表2。

图2 砂沟井田煤储层评价指标体系图

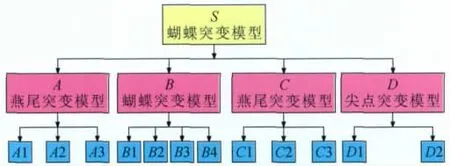
图3 砂沟井田煤储层评价突变模型图

2.2 指标控制变量的无量纲化

利用式（4）对煤储层有利指标采用无量纲化，求得结果见表2。

当指标值与对储层有利时，si为指标值，ci为样本指标最大值；当指标值与对储层不利时，si为指标值倒数值，ci为样本指标倒数最大值。

2.3 参数归一化

按照突变理论多准则评价方法、采用突变系统的归一公式，按指标层、准则层、目标层逐层计算突变隶属函数，具体计算过程如下：

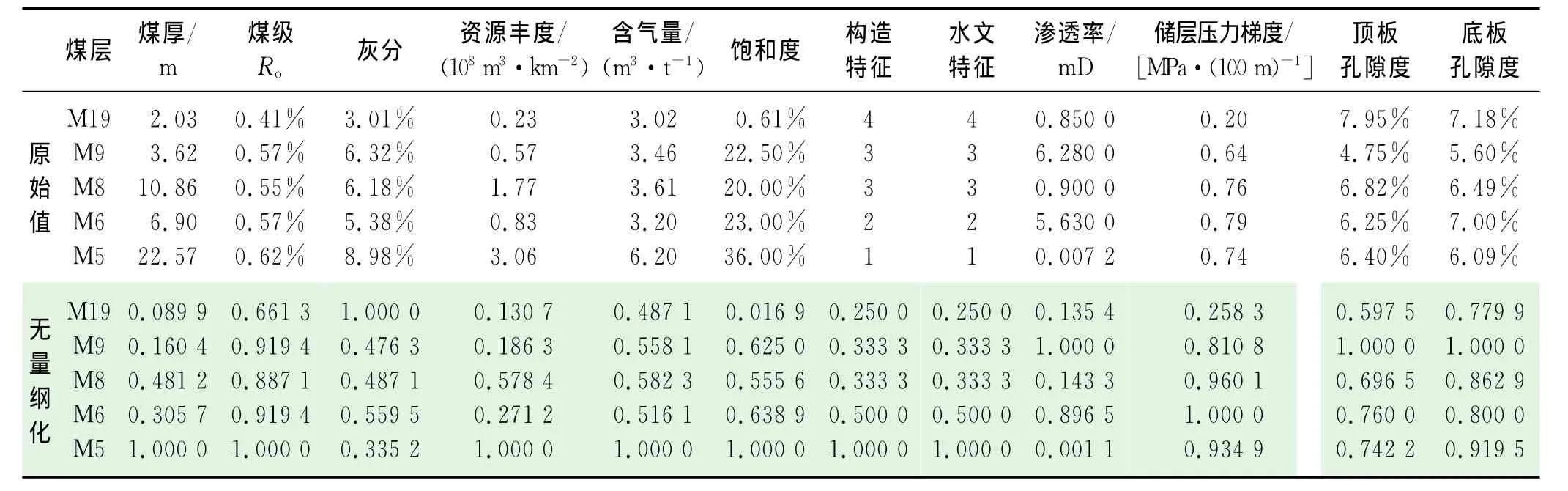
表2 研究区评价指标统计表

如图2、3中指标层含气量A1、资源丰度A2和含气饱和度A3构成燕尾突变，根据式（2）计算M19号煤层：

指标层相互作用共同对准则层作用，按互补原则，取均值得：

A＝ （0.300 0＋0.661 3＋1.0000）／3＝0.723 7

B1、B2、B3、B4构成蝴蝶突变；C1、C2、C3构成燕尾突变；D1、D2构成尖点突变，计算得到准则层。准则层A、B、C、D构成蝴蝶突变，计算得S＝0.857 2。同理可求得其他主采煤层煤层气储层评价值（表3）。

2.4 综合评价

按照最大隶属度函数得出煤层气有利储层排序，从计算结果（表3）可以得出砂沟井田煤层气储层中M5号煤层含气量、资源丰度较高，开采性能、储层特征较好，储层相对有利，M19号煤层则相对不利。与模糊评判得出结果优劣程度排序一致（表3），验证了突变理论评价法的可行性及正确性。

3 结论

1）综合考虑影响煤层气勘探开发潜力的资源特征、开采性能、煤层特征和构造特征多种指标因素，根据层次分析法原理，建立由目标层、准则层和指标层组成的砂沟井田煤层气储层评价指标多层次结构。

表3 砂沟井田储层突变评价结果表

2）运用各指标间的相互关系确定指标间的重要性排序，确定了突变模型，对砂沟井田煤层气储层进行了评价，评价结果与模糊评判结果一致，表明突变理论可用于煤层气储层评价，且评价结果较为准确。

[1]王勃，孙粉锦，李贵中，等.基于模糊物元的煤层气高产富集区预测——以沁水盆地为例[J].天然气工业，2010，30（11）：22－25.WANG Bo，SUN Fenjin，LI Guizhong，et al.Prediction of prolific CBM zones with the fuzzy matter element method：A case study of the Qinshui Basin[J].Natural Gas Industry，2010，30（11）：22－25.

[2]杨欣超，桑树勋，方良才，等.灰色关联分析在煤层气储层评价中的应用[J].西安科技大学学报，2010，30（2）：202－206.YANG Xinchao，SANG Shuxun，FANG Liangcai，et al.Application of grey relational analysis to evaluation of coalbed methane reservoir[J].Journal of Xi′an University of Science and Technology，2010，30（2）：202－206.

[3]雷能忠.基于RBF神经网络的煤储层随机建模[J].煤炭学报，2012，37（7）：1144－1149.LEI Nengzhong.Stochastic simulation of coalbed methane reservoir by radial basis function neural network[J].Journal of China Coal Society，2012，37（7）：1144－1149.

[4]张松航，汤达祯，唐书恒，等.鄂尔多斯盆地东缘煤层气储集与产出条件[J].煤炭学报，2009，34（10）：1297－1304.ZHANG Songhang，TANG Dazhen，TANG Shuheng，et al.Preservation and deliverability characteristics of coalbed methane in east margin of Ordos Basin[J].Journal of China Coal Society，2009，34（10）：1297－1304.

[5]邵龙义，文怀军，李永红，等.青海省天俊县木里煤田煤层气有利区块的多层次模糊数学评价[J].地质通报，2011，30（12）：1896－1903.SHAO Longyi，WEN Huaijun，LI Yonghong，et al.Assessment of favorable areas for coalbed methane resources exploration in the Muli Coalfield of Qinghai Province based on multi－layered fuzzy mathematics[J].Geological Bulletin of China，2011，30（12）：1896－1903.

[6]凌复华.突变理论及应用[M].上海：上海交通大学出版社，1987.LING Fuhua.The theory and application of catastrophe theory[M].Shanghai：Shanghai Jiaotong University Press，1987.

[7]李绍飞，孙书洪，王向余.突变理论在海河流域地下水环境风险评价中的应用[J].水利学报，2007，38（11）：1312－1317.LI Shaofei，SUN Shuhong，WANG Xiangyu.Application of catastrophe theory to risk assessment of groundwater environment for river basin[J].Journal of Hydraulic Engineering，2007，38（11）：1312－1317.

[8]都兴富.突变理论在经济领域的应用（下册）[M].成都：电子科技大学出版社，1994.DOU Xingfu.The application of catastrophe theory in economic field（Vol.Ⅱ）[M].Chengdu：University of Electronic Science ＆ Technology Press，1994.

[9]戴勇，李正文，吴大奎.突变论在地震资料储层预测中的应用[J].天然气工业，2006，26（6）：47－49.DAI Yong，LI Zhengwen，WU Dakui.Application of catastrophic theory to seismic reservoir prediction[J].Natural Gas Indusrty，2006，26（6）：47－49.

[10]何沙，吉安民，杨喆，等.安全流变—突变模型在井喷事故中的应用分析[J].天然气工业，2011，31（4）：109－112.HE Sha，JI Anmin，YANG Zhe，et al.Application of Safety Rheology－Mutation Models in well blowout accidents[J].Natural Gas Indusrty，2011，31（4）：109－112.

[11]冯润民.大学生群体行为突变机理分析及对策研究[J].北京交通大学学报：社会科学版.2010，9（2）：110－114.FENG Runmin.An analysis on the revulsion mechanism of students’collective behaviors and their countermeasures[J].Journal of Beijing Jiaotong University：Social Sciences Edition，2010，9（2）：110－114.

[12]赵焕臣，许树柏，和金生.层次分析法——一种简易的新决策方法[M].北京：科学出版社，1986.ZHAO Huanchen，XU Shubai，HE Jinsheng.Stratification analysis method －a new simple decision making method[M].Beijing：Science and Technology Press，1986.