基于粒子群优化算法的光伏阵列MPPT
王 平,卞建龙
(河海大学 能源与电气学院,江苏 南京 211100)
基于粒子群优化算法的光伏阵列MPPT
王 平,卞建龙
(河海大学 能源与电气学院,江苏 南京 211100)
针对光伏阵列在阴影下具有多个最大功率点,而传统的优化算法不能有效跟踪全局最大功率点的问题,提出了一种基于粒子群优化算法的跟踪算法,在Matlab平台上利用M函数对光伏阵列和跟踪算法进行编程。仿真结果表明:该控制算法不仅具有跟踪速动快、稳态精度高的特点,而且能够跟踪全局最大功率点,比传统的优化算法更有优势。
局部阴影;最优梯度法;粒子群优化算法;最大功率点跟踪
光伏发电作为一种新兴的发电形式,因其资源节约型、环境友好型的优点备受关注与重视,然而转换效率低下[1]一直是制约其发展的重要因素之一。由于周围建筑物、树木以及太阳照射方位的影响会造成光伏阵列表面所接受的光照不均匀,导致局部阴影现象的产生,光伏阵列输出的P-U曲线上会出现多个局部峰值,若没有良好的最大功率点跟踪算法,将导致光伏发电的转化效率严重低下。因此研究局部阴影下光伏阵列的数学模型与最大功率点跟踪(Maxiumum Power Point Tracking,MPPT)对于提高光伏阵列的发电效率和加快光伏发电发展有着重大意义。
1 局部阴影下光伏阵列运行特性分析
1.1 光伏电池数学模型
供应商一般提供光伏模块在标准条件下测试得到的4个重要技术参数:短路电流Isc、开路电压Voc、最大功率点电流Im、最大功率点电压Vm。通过给定的这4个参数,文献[2]给出了光伏模块工程用的数学模型(误差6%以内):

其中I、U分别为光伏模块的输出电流与端电压;
式(1)中 C1、C2的表达式[2]为:
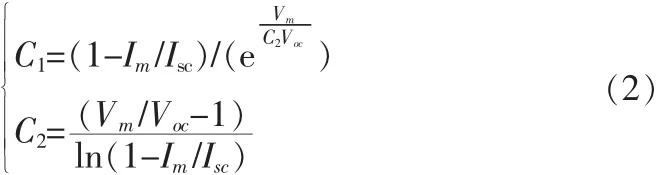
下表给出一个140 W光伏电池模块的技术参数:

表1 140W光伏模块的技术参数Tab.1 Technical parameters of 140 W PV module
1.2 串联型光伏阵列的运行特性
假设2个140 W的光伏电池模块直接串联 (如图1所示),第一个模块辐射强度为1 000 W/m2,第二个模块由于局部阴影的原因平均辐射强度仅为第一个模块的2/3。由文献[3-5]可知,对于串联型的光伏阵列,在光伏模块两端并联旁路二极管能够防止处在阴影下的光伏模块成为负载,提高阵列在局部阴影下的功率输出能力,降低能量的损失,防止电池模块的损坏。串联型光伏阵列结构。
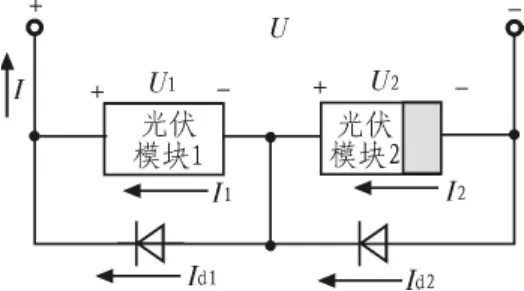
图1 串联型光伏阵列结构Fig.1 Serial pv array struct
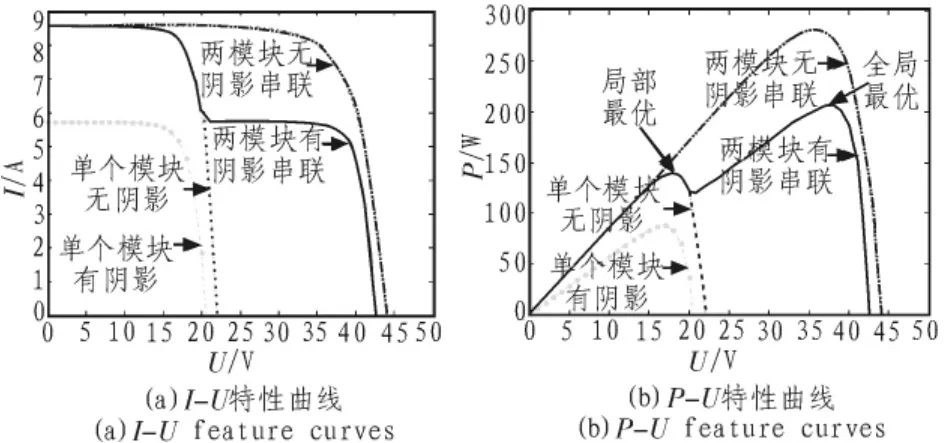
图2 局部阴影下串联型光伏阵列的输出特性Fig.2 Serial pv array output characteristic under patial-shade
设光伏模块1的短路电流和工作电流分别为Isc1、I1,光伏模块2的短路电流和工作电流分别为Isc2、I2。当阵列工作电流比较大时,模块1流过的电流比模块2流过的电流大,则模块2对应旁路二极管导通,此时仅由光伏模块1输出功率给负载;当阵列工作的电流小于模块2的短路电流的时候,此时由模块1和模块2同时输出功率给负载。因此,串联型光伏阵列的输出特性可用以下的分段函数来表示:
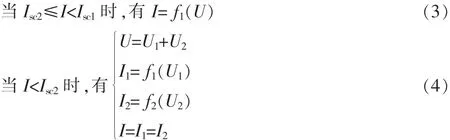
其中:f1为模块1的伏安特性函数;f2是模块2的伏安特性函数;U1、U2分别为模块 1、2的端电压;I为光伏阵列的电流;U为光伏阵列的端电压,利用Matlab进行仿真于是得到串联型光伏阵列在局部阴影下的输出特性曲线如图2所示。
2 最速上升算法MPPT仿真
2.1 最速上升算法在MPPT中的应用
针对固定步长占空比扰动法存在跟踪精度与速度不能兼顾的问题,采用差商变尺度法来优化功率扰动法,使占空比步长能够在线调整[6],以满足跟踪速度和精度的要求。
最速上升算法步骤:
Step1:给定初始点 D0∈(0,1],D1=D0+d,其中 d 为步长因子;
Step2:根据 D1情况下所对应的 P1,D0情况下所对应的P0,根据公式 λ=(P1-P0)/(D1-D0);
Step3:比较 P1和 P0的大小,如果 P1>P0则令 D0=D1、P0=P1;
Step4:若 λ≤ε,则输出占空比 D1=D0,否则输出占空比D1=D0+λ*d;
Step5:返回Step2继续迭代;
2.2 最速上升算法MPPT仿真
采用最速上升算法对上述串联模型进行MPPT仿真,其中采样频率为1 kHz,负载阻值为30 Ω,取初始点D0=0.7和D0=0.5得到的仿真曲线如图3所示。
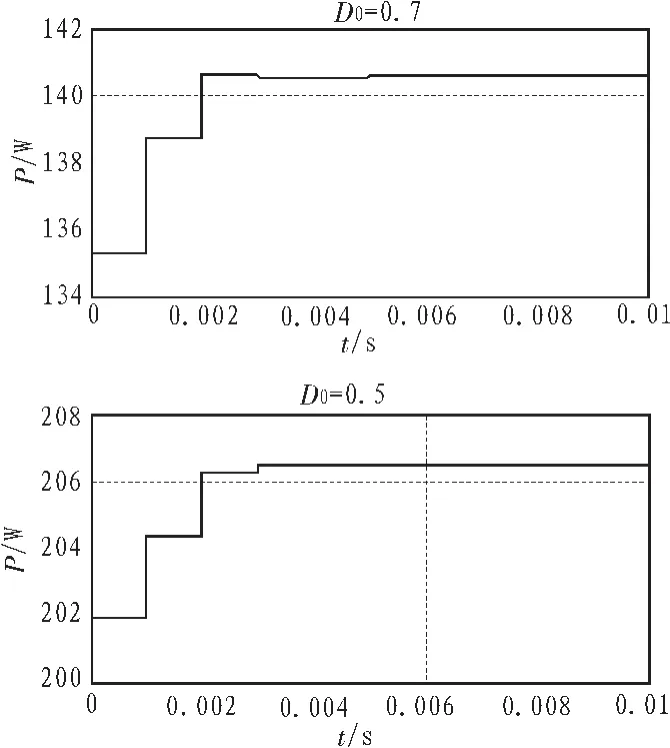
图3 阴影下最速上升算法MPPT仿真Fig.3 MPPT simulation with methold of steepest ascent under partial-shade
当初始值为0.7时,搜索到最大功率约为140.5 W,当初始值为0.5时,跟踪到最大功率约为206.5 W。从仿真结果可以看出,用最速上升算法进行MPPT,得到的结果是靠近初始值附近的最大功率点,即局部最优点。因而在多峰的情况下,若使用最速上升算法可能会大大降低光伏阵列的输出效率,满足不了MPPT的要求。
3 粒子群算法MPPT仿真
3.1 粒子群算法在MPPT中的应用
在多峰情况下,最速上升法只能搜索到光伏阵列局部最大功率点,导致光伏阵列输出效率低,因此采用传统的局部优化算法难以搜索到全局最大功率点。粒子群算法(Particle Swarm Optimation,PSO)是一种新兴的群智能优化算法[7],它的基本思想是通过群体中个体之间的协作与竞争来寻找最优解,群体中的每个个体不仅可以从自己的经验中受益,而且可以从相邻个体以往的经验中受益。因此,PSO算法不仅有局部优化的能力也有全局优化的能力,可以用于多峰情况下的最大功率点跟踪。
算法[7]中,粒子i在第 k次飞行中以速度 vi(k)在搜索空间中飞行至位置Si(k),则在第k+1次飞行中飞行的速度vi(k+1)是根据 2个最优值来更新自己上一次的速度 vi(k)的:一个是粒子本身飞行到此刻所找到的最优值,即个体最优值pbesti;另一个是整个粒子群体飞行到此刻所找到的最优值,即全体最优值gbest。获得vi(k+1)后,第k+1次所飞行至的位置 si(k+1)则可由 vi(k+1)来更新。 在飞行的过程中,粒子 i由si(k)移动至 si(k+1)的过程示意图如图 4 所示。
速度、位置、个体最优值、全局最优值由公式(5)、(6)、(7)、(8)进行更新:
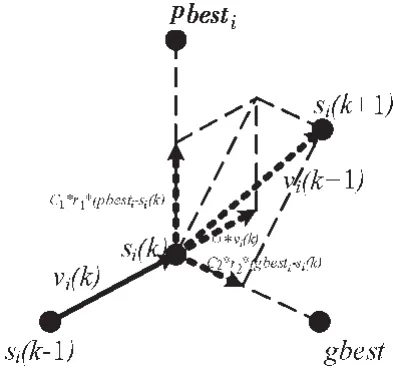
图4 粒子移动示意图Fig.4 Schematic diagram of partical movement
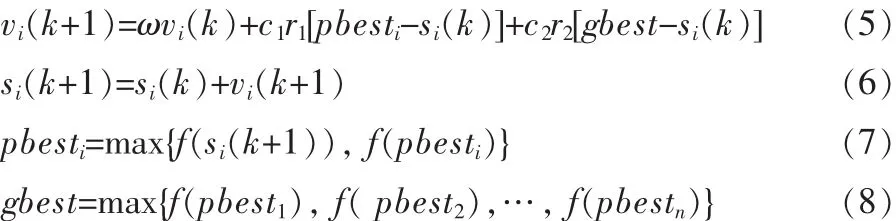
其中:i=1,2,……n,n为群体中的粒子数;ω是惯性权重;c1、c2为学习因子;r1、r2为 0~1 之间随机分布的随机数;目标函数f为输出的功率;s为占空比;v为占空比变化的步长。
3.2 粒子群算法的相关设置
3.2.1 惯性权重的设置
考虑到惯性权重影响PSO的全局和局部寻优能力,较大的惯性因子有利于跳出局部极值,提高跟踪的速度,而较小的惯性权重有利于进行精确的局部搜索,提高跟踪的精度。按照这样的原则,本文中惯性权重ω随迭代次数k变化的公式如下:

3.2.2 算法迭代停止设置
为了使算法能够捕捉到外界环境的变化以重新启动算法,当迭代到第k次时,N个粒子输出端电压相对于此时全局最优电压值的方差满足D(k)<1时,则停止算法的迭代,占空比按照最终得到的全局最优值恒定输出[8]。其中D(k)的计算公式为:

当粒子群算法迭代到7次左右的时候,已经基本上完成了最大功率点跟踪。从仿真结果可以看出,用本文提出的pso算法进行MPPT,能避免算法收敛于局部最优值,具有较好的收敛速度和精度,在多峰的情况下,能够满足全局最大功率点的跟踪。)
4 结 论
3.2.3 算法重新初始化设置
在算法在最大功率点稳定运行一定时间后,光照强度或阴影范围却突然发生了剧烈变化的情况下,需要重新初始化算法[9-11],使光伏阵列重新稳定运行在新的最大功率点。当满足以下公式,就认为外界环境发生了剧烈的变化,需重新启动算法。
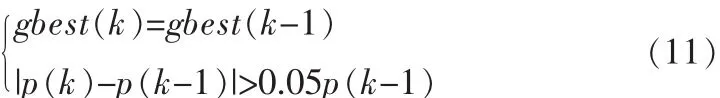
在外界虽环境缓慢变化,但是通过较长的时间的积累,外界环境却发生巨大变化的情况下,式(11)却不能反应出这样的情况,此时加入算法定时重启的策略,设定时间为30 s。
3.3 粒子群算法MPPT仿真
采用粒子群算法对上述串联模型进行MPPT仿真,其中粒子数为10个,采样频率为1 kHz,负载阻值为30 Ω,得到的仿真结果如图5、6所示。

图5 粒子运动示意图Fig.5 Schematic diagram of partical movement

图6 功率跟踪曲线Fig.6 Power tracking curves
传统的光伏阵列MPPT[6,12]仅仅建立在单峰情况下的最大功率点跟踪,更不用提及局部阴影下MPPT策略的研究。本文在苏建徽等建立的工程用的数学模型[2]的基础上,研究了光伏模块在串联情况下的数学模型,并以两个组件的串联模型为例发现了局部阴影情况下P-U曲线呈现多峰的现象。然后应用此模型,采用最速上升法进行最大功率点跟踪的研究,发现跟踪结果是否为全局最大功率点取决于初始跟踪点的设置,故不能保证每次都能有效跟踪到最大功率点。针对此问题,本文将粒子群优化算法应用于最大功率点的跟踪,发现此算法满足了全局最大功率点跟踪的要求,比传统的优化算法更有优势。
[1]赵福鑫,魏彦章.太阳电池及其应用[M].北京:国防工业出版社,1985.
[2]苏建徽,余世杰,赵为,等.硅太阳电池工程用数学模型[J].太阳能学报,2001,22(4):409-412.
SU Jian-hui,YU Shi-jie,ZHAO Wei,et al.Investigation on engineering analytical model of silicon solar cells[J].Acta Energiae Solaris Sinica,2001,22(4):409-412.
[3]宋菁,徐青山,祈建华,等.光伏电池运行失配模式及特性分析[J].电力系统及其自动化学报,2010,6(22):119-123.
SONG Jing,XU Qing-shan,QI Jian-hua,et al.Solar cell run in mismatch mode and feature analysis[J].Proceeding of the CSU-EPSA,2010,6(22):119-123.
[4]刘邦银,段善旭,康勇.局部阴影条件下光伏模组特性的建模与分析[J].太阳能学报,208,2(29):188-192.
LIU Bang-yin,DUAN Shan-xu,KANG Yong.Model and analysis of photovoltaic module under partial shading[J].Acta Energiae Solaris Sinica,208,2(29):188-192.
[5]刘晓艳,祁新梅,郑寿森,等.局部阴影条件下光伏阵列的建模与分析[J].电网技术,2010,34(11):192-197.
LIU Xiao-yan,QI Xin-mei,ZHENG Shou-sen,et al.Model and analysis of photovoltaic array under partial shading[J].Power System Technology,2010,34(11):192-197.
[6]王夏楠.独立光伏发电系统及其MPPT的研究[D].南京:南京航空航天大学,2008.
[7]Kennedy J,Eberhart R.Particle swarm[J].Optimization in Proc.of IEEE International Conference on Neural Networks,1995(1):1942-1948.
[8]朱艳伟,石新春,但扬清,等.粒子群优化算法在光伏阵列最大功率点跟踪中的应用 [J].中国电机工程学报,2012,32(4):42-48.
ZHU Yan-wei,SHI Xin-chun,DAN Yang-qing,et al.Application of PSO algorithm in global mppt for pv array[J].Proceedings of the CSEE,2012,32(4):42-48.
[9]胡成玉.面向动态环境的粒子群算法研究[D].武汉:华中科技大学,2010.
[10]高尚,杨静宇.粒子群算法及其应用[M].北京:中国水利水电出版社,2006.
[11]徐星.热力学粒子群优化算法研究及其应用[M].天津:天津大学出版社,2011.
[12]黄舒予,牟龙华,石林.自适应变步长MPPT算法[J].电力系统及其自动化学报,2011,23(5):26-30.
HUANG Shu-yu,MU Long-hua,SHI Lin.Adaptive variable step size MPPT algorithm[J].Proceeding of the CSU-EPSA,2011,23(5):26-30.
MPPT of photovoltaic array based on PSO algorithm
WANG Ping,BIAN Jian-long
(College of Energy and Electric, Hohai University, Nanjing 211100, China)
In order to resolve the problem that pv array under partial-shading has multiple mpps (maximum power points) and the conventional optimization algorithms can't effectively track the global mpp,a control algorithm based on particle swarm optimization algorithm (PSO) was proposed in the paper.In the Matlab environment, the photovoltaic array model and the control strategy is programmed with M-function The simulation results show:the algorithm not only has the features of Good dynamic performance, high accuracy of steady-state, but also can track the global mpp.It is proved that PSO method is superior to the conventional optimization algorithms.
partial-shading;optimum gradient method;PSO;MPPT
TM615
A
1674-6236(2013)08-0128-04
2013-03-13稿件编号201303165
王 平(1962—),男,江苏南京人,硕士,副教授。研究方向:电力系统自动化技术。

