最小平均等待时间约束下的备件库存优化模型

王玉文，金家善，陈砚桥，魏曙寰

(海军工程大学动力工程学院，湖北武汉430033)

最小平均等待时间约束下的备件库存优化模型

王玉文，金家善，陈砚桥，魏曙寰

(海军工程大学动力工程学院，湖北武汉430033)

应用装备平均等待备件时间与备件的延期交货量之间的数学关系，构建以装备平均等待备件时间为约束条件的库存优化模型。然后运用边际效应分析方法描述了备件库存优化流程。最后以算例的形式，对备件库存量进行预测，验证优化模型的可信性。

平均等待备件时间;延期交货量;边际效应;优化

0 引言

备件数量的确定是装备综合保障的一个重要组成部分，它直接决定装备的战备完好和任务的持续能力。制定科学的备件存储模型，确定合理的备件储备数量，既能满足装备的使用要求，又能大幅度降低备件的全寿命周期费用。为了确定可更换部件最优的储备数量，需要建立备件数量与系统性能的关联关系。目前，国内外对备件库存模型作了大量研究。文献［1－3］研究了备件保障概率约束下的备件数量模型。文献［4］论述了以装备可用度为约束条件的备件库存优化算法。但是，这些模型并没有建立装备因等待备件而导致的停机时间与备件库存量之间的关系。

在影响装备可用度的3种主要停机时间要素中，等待备件所造成的停机时间已经超过了修复性维修停机时间和预防性维修停机时间［5］。因此，非常有必要对装备等待备件的时间加以约束。本文以费用作为优化目标，选取装备的平均等待备件时间作为约束条件。针对寿命分布服从指数分布的备件，运用边际效应分析方法，计算装备系统中不同类型备件最优的储备数量。

1 模型约束条件

在一个供货周期内，装备对某种类型备件产生的需求量超过该种备件的库存数量和已修复的备件数量之和时，超出的备件需求得不到满足就会导致延期交货。考虑到只有存在延期交货，才会出现装备等待备件的情况，因此平均等待备件的时间和备件的延期交货量有直接关系。要想得到平均等待备件的时间，必须首先计算备件的延期交货量。备件的延期交货量是指当装备产生备件需求时，没有被立即满足的备件的数量，而这些备件需求要等待一段时间后才能被满足。

备件的延期交货量EBO的计算公式为

式中：p(x)为部件有x个单元处于维修(再供应)过程的稳态概率;s为备件的库存数量。

当备件的故障间隔时间服从指数分布且其均值为常数时，则备件的寿命分布服从均值为λt的泊松分布，可由下式表示：

式中：λ为备件需求率;t为备件周转时间。将式(2)代入式(1)，可得：

平均等待备件的时间T就等于备件延期交货量与备件需求率的比值，可由下式表示［6］：

若装备系统由n种不同类型的备件构成，则由式(4)可得系统中第i种备件在库存量为si时平均等待备件时间Ti(si)的计算公式为

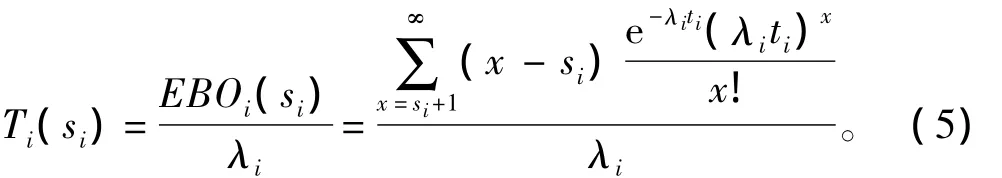
式中：si为系统中第i种备件的库存数量;λi为第i种备件的需求率;EBOi(si)为第i种备件在库存数量为si时的延期交货量。

装备平均等待备件时间T的计算公式为［6］：

式中：SDTi(si)表示编号为i的备件平均等待时间。

2 备件库存数学模型

选取费用作为优化目标，在保证装备系统平均等待备件时间低于某一固定值Tm的前提下，使系统级的备件费用最低。数学规划公式如下：

式中ci为系统中第i种备件的单价。

3 边际效应分析方法

边际效应分析是一种渐进的优化算法，用于分配短缺资源来获取最大的效益。在设定的约束条件下依次进行迭代，直到满足系统最终的目标值为止。边际效应分析方法的思想就是，每种备件的数量每次只增加1个，比较增加哪种备件所带来的优化效益与该备件费用的比值最大，即购买该备件的效费比最高。用边际效应分析方法求解本问题的步骤如下：

1)确定装备系统中备件的品种和最初的储备数量，初始的控制变量si(i=1，2，…，n)的值全部设置为0。

2)确定需要调整的控制变量，寻找最大的边际效应ΔPi(si)/ci，其计算公式为：

3)分别计算n类备件的ΔPi(si)/ci的值，将最大值对应的备件数量加1。

4)根据所有备件的库存量si，计算相应的备件延期交货量，进而计算系统的平均等待备件时间，若小于等于目标值Tm，则迭代完成，否则，进入步骤2继续迭代。

用边际效应分析所建立的数学模型流程图如图1所示。

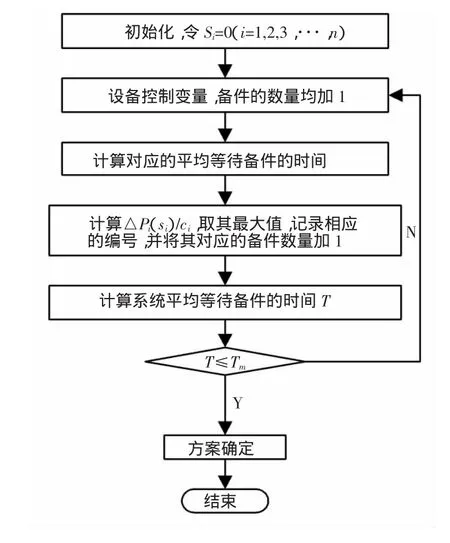
图1 边际效应分析流程图Fig.1 Margin utility analysis flow chart

4 实例分析

某装备系统由 LRU1，LRU2，LRU3，LRU4，LRU5，LRU6和LRU7共7种类型的备件构成，备件的各项参数如表1所示。

表1 备件相关数据Tab.1 Relative data of the spare parts

运用边际效应分析方法对备件的库存数量进行优化设计，分析过程如表2所示。在进行了28轮迭代 之 后， LRU1， LRU2， LRU3， LRU4， LRU5，LRU6和LRU7的库存数量分别为4，4，3，6，3，5，3，计算得到的系统平均等待备件时间为0.902天，小于设定值1天。

通过边际效应分析方法，由备件的需求率、周转时间和单价等已知信息，在装备最小平均等待备件时间的约束下，确定了不同种类的备件各自的库存量。

表2 边际效应分析过程数据表Tab.2 Margin utility analysis of process data sheet

5 结语

本文分析了装备平均等待备件时间与备件的库存量和备件需求率之间的函数关系，构建了以装备平均等待备件时间为约束的库存优化模型，并运用边际效应分析方法对备件的库存量进行优化设计，具有重要指导意义。本文没有考虑装备因等待备件而导致的停机所造成的损失，在今后的工作中会做进一步研究。

［1］程海龙，康锐，肖波平，等．备件满足率约束下的备件模型［J］．系统工程与电子技术，2007，29(8)：1314 －1316．

CHENG Hai-long，KANG Rui，XIAO Bo-ping，et al．Spare model under the constraint of spare sufficiency［J］．Systems Engineering and Electronics，2007，29(8)：1314 －1316．

［2］王乃超，康锐．基于备件保障概率的多级库存优化模型［J］．航空学报，2009，30(6)：1043 －1047．

WANG Nai-chao，KANG Rui．Optimization of multi-echelon repairable item inventory systems with fill rate as objietive［J］．Acta Aeronautica Astronautica Sinca，2009，30(6)：1043－1047．

［3］程海龙，康锐，龙军，等．基于边际效应的备件保障概率库存优化模型［J］．先进制造与管理，2008，27(11)：37 －39．

CHENG Hai-long， KANG Rui， LONG Jun， etal．Optimization model on support probability of spare part inventory based on margin utility［J］．Advanced Manufacture and Management，2008，27(11)：37 －39．

［4］毛德军，李庆民，张志华．以装备可用度为中心的保障方案优化方法［J］．兵工学报，2011，32(5)：636 －640．

MAO De-jun，LI Qing-min，ZHANG Zhi-hua．An optimizing method for availability-centric equipment support plan［J］．Acta Armamentarii，2011，32(5)：636 －640．

［5］杨秉喜，李金国，张义芳，等．GJB4355，备件供应规划要求实施指南［S］．FL0113，2005．

［6］王乃超，康锐．多约束条件下备件库存优化模型及分解算法［J］．兵工学报，2009，30(2)：247 －251．

WANG Nai-chao，KANG Rui．An optimization model for inventory spares under multi-constraints and its decomposition algorithm［J］．Acta Armamentarii，2009，30(2)：247－251．

［7］王佩高，金家善．随舰备件动态管理及备件数量计算模型［J］．海军工程大学学报，2005，17(3)：103 －106．

WANG Pei-gao，JIN Jia-shan．A calculation model and dynamic management for quantity of spare part on warship［J］．Journal of Naval University of Engineering，2005，17(3)：103－106．

［8］KENNEDY W J，PATTERSON J W，FREDENDALL L D．An overview of recent literature on spare parts inventories［J］．Int J Production Economics，2002，76(2)：201 －215．

［9］康锐，李瑞莹，王乃超，等．可靠性与维修性工程概论［M］．北京：清华大学出版社，2010．

［10］王乃超，康锐，程海龙．基于马尔科夫过程的备件库存动态特性分析［J］．兵工学报，2009，30(7)：984 －988．

WANG Nai-chao，KANG Rui，CHENG Hai-long．Study on the dynamic characteristics of spare inventory based on markov process［J］．Acta Armamentarii，2009，30(7)：984－988．

An optimization model for inventory sapares under the minimum average time for waiting spares

WANG Yu-wen，JIN Jia-shan，CHEN Yan-qiao，WEI Shu-huan
(Power Engineering College，Naval University of Engineering，Wuhan 430033，China)

It expounds the mathematical relationship between the minimum average time for waiting spares and the expected number of backorders in this article．Then，the inventory optimization model is created under the minimum average time for waiting spares of the equipment．Then，optimization approach of spares inventory is described with margin analysis．Finally，predict the number of spares inventory through particular case applying，validate the credibility of the optimization model．

minimum average time for waiting spares;expected number of backorders;margin utility;optimization

TP391．9

A

1672－7649(2013)12－0132－03

10.3404/j.issn.1672－7649.2013.12.027

2013－03－28;

2013－05－08

王玉文(1991－)，男，硕士研究生，研究方向为舰船综合保障工程。