状态变化和学习行为下的最优资产组合选择

陈志英

西南政法大学 经济学院，重庆 401120

状态变化和学习行为下的最优资产组合选择

陈志英

西南政法大学 经济学院，重庆 401120

针对金融资产收益率序列的非线性动态变化和投资者参数确定的传统假设，考虑状态变化的最优资产组合选择以及参数不确定性下投资者学习行为对最优资产组合选择的影响，运用马尔科夫机制转换模型刻画市场状态变化，采用贝叶斯学习准则描述投资者的学习行为，建立状态变化和投资者学习行为下资产组合选择的离散时间模型，使用期望最大化算法和动态最优化方法给出模型的参数估计，使用蒙特卡罗方法模拟投资者的资产组合选择行为。研究结果表明，中国金融市场存在明显的结构性动态变化，可以将市场分为牛市和熊市。在短期，当市场处于熊市时，投资者将全部财富投资于债券，不投资于股票，但市场处于牛市时股票的投资比重会大大增加;在长期，牛、熊市下股票和债券的权重会稳定在某个水平。市场状态的不确定性造成投资者产生对冲不确定性风险的需求，当市场向好时，投资者学习行为导致其投资于更多的风险资产;当市场状态无法确定时，投资者对股票的投资更为谨慎。考虑市场状态变化的投资组合选择能够提高投资者的总体效用。

最优资产组合选择;状态变化;牛、熊市;贝叶斯学习;效用成本

1 引言

标准投资组合理论假设金融资产的收益率由一个参数稳定的线性过程生成，同时假设反映市场风险的参数在整个投资期限内不变。但大量的实证研究表明，金融资产的收益率常常表现出非线性、动态的结构性变化。类似于经济周期变化，资本市场也存在牛市和熊市，并在牛市和熊市的不断更替中演进。在不同的市场状态下，资产的收益率和风险是不对称的。Longin等［1］和 Ang等［2］发现在市场下跌时，资产收益率明显下降，资产波动率以及各资产间的相关性会显著高于正常情况;刘琛［3］发现中国资本市场也存在类似特征。

传统理论假设投资者准确地知道与资产收益率相关的各种参数(如均值和方差)，但由于信息不对称和投资者自身因素限制，投资者对参数是不确定的，但他们并非一无所知，他们可以利用获得的市场信息对参数进行推断估计，基于估计值给出最优决策，并利用新的信息更新参数估计，调整组合头寸。换句话说，投资者具有学习能力。Pastor等［4］认为学习行为可以解释很多最初令人困惑的金融现象。

针对这些现实，本研究通过引入马尔科夫机制转换模型和贝叶斯学习，建立状态变化和投资者学习行为下的最优资产组合选择模型，使用蒙特卡罗方法模拟投资者的最优资产组合选择行为，分析在不同的市场状态下投资者的最优资产组合选择行为和学习行为对状态变化下的资产配置产生的影响以及考虑状态变化和学习行为的组合模型对投资者总体效用的影响。

2 相关研究评述

近年来，很多学者对状态变化下的最优资产组合选择进行研究。由于马尔科夫机制转换模型包含多个结构方程，可以刻画宏观经济变量或金融时间序列变量在不同状态下的变化及转换过程，而且能够很好地描述资产收益率的尖峰肥尾、异方差和非对称相关系数等性质，因此许多学者利用马尔科夫机制转换模型刻画金融时间序列分布的结构性变化。Ang等［5-6］和 Liow 等［7］运用马尔科夫机制转换模型研究状态变化下的国际化资产组合选择，研究结果表明最优投资权重依赖于各种不同的市场状态和投资期限，考虑到机制转换的国际分散化投资能够明显提高投资者的效用，在样本外机制转换投资择时组合策略也优于静态模型。但这些学者假设市场状态是可观测的，与现实不符。Guidolin等［8-9］推广Ang等［5-6］的模型，假设投资者并不知道当前的市场状态，他们只能通过观察市场上各资产的价格去推断当前的市场状态，利用蒙特卡罗方法模拟分析美国股票和债券市场的机制转换特征对资产配置的经济意义。运用同样的方法，Guidolin等［10］将美国股票市场组合、规模组合和价值组合收益率分成4个机制，在幂效用框架下说明4种机制如何影响投资者在市场组合、规模组合、价值组合和无风险资产之间的配置;Guidolin等［11］还考虑了收益率的高阶矩的机制转换特征对资产配置的影响;Tu［12］研究机制转换以及参数不确定情形下的最优投资组合问题，实证结果表明忽略市场机制会造成每年2%的福利损失，市场下跌时损失高达10%。中国学者主要对状态变化下的资产定价模型进行理论和实证研究，如李卓等［13］、苏涛等［14］和赵鹏等［15］的研究。

关于投资者学习行为对资产组合选择的影响，目前很少有学者从市场状态变化这个角度进行研究，一般都是单独考虑投资者学习行为下的资产组合选择。研究的主要范式为，将不可观测的参数看做是一个随机变量，而不再是某个固定的数值，投资者首先对这些参数设定一个确定的主观先验分布，然后运用贝叶斯准则结合当前已有信息获得参数或模型的后验分布，投资者依据后验分布进行投资决策，如 Hoeting 等［16］、Wachter［17］、孟卫东等［18］和杨朝军等［19］的研究。Honda［20］同时考虑市场状态变化和投资者学习行为两种情形，用隐马尔科夫链刻画不可观测的市场状态，利用滤波理论描述投资者的学习行为，研究连续时间下最优消费和投资组合问题，并用数值方法计算幂效用下的最优投资和消费，研究结果表明市场状态的不确定性让投资者产生对冲市场状态不确定的风险规避需求。

Honda［20］建立的是连续时间模型。在连续时间框架下研究最优资产组合选择往往能得到一些非常有用的结论，但连续交易在现实中是不太可能的。因此，本研究从离散时间角度进行分析，以中国资本市场为研究样本，利用马尔科夫机制转换模型刻画非线性的市场状态变化，引入贝叶斯学习准则描述投资者的学习行为，采用蒙特卡罗方法模拟市场状态变化以及投资者学习下静态和动态的投资者决策行为。

3 马尔科夫机制转换向量自回归模型

假设N个风险资产的超额收益率的时间序列为rt，rt=(r1t，r2t，…，rNt)，满足 MS(K)-VAR(m)过程，即

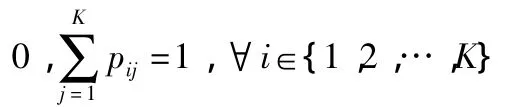
进一步地，将(1)式转化为均值调整形式，即

采用Hamilton［21］给出的马尔科夫机制转换模型的极大似然估计法和期望最大化算法(E-M算法)估计参数。

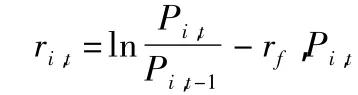
表1列出上证综指和中信全债超额收益率的描述性统计。由表1可知，股票超额收益率的波动率明显高于债券超额收益率的波动率，偏度和峰度表明二者都是尖峰肥尾分布，ADF检验表明二者都是平稳序列，滞后20阶的 Ljung-Box检验显示，中信全债和上证综指的超额收益率在5%置信水平均存在序列自相关。上证综指超额收益率与中信全债超额收益率的相关系数为-0.021，表现为负相关。

表1 描述性统计Table 1 Descriptive Statistics

本 研 究 运 用 Krolzig［22］的 MSVAR 软 件 包 在Givewin平台上对模型进行估计。根据AIC准则、HQ准则、SC准则和对数似然值综合判断，本研究发现MS(2)-VAR(1)模型的解释能力较强。表2和表3分别给出单状态和双状态的估计结果。

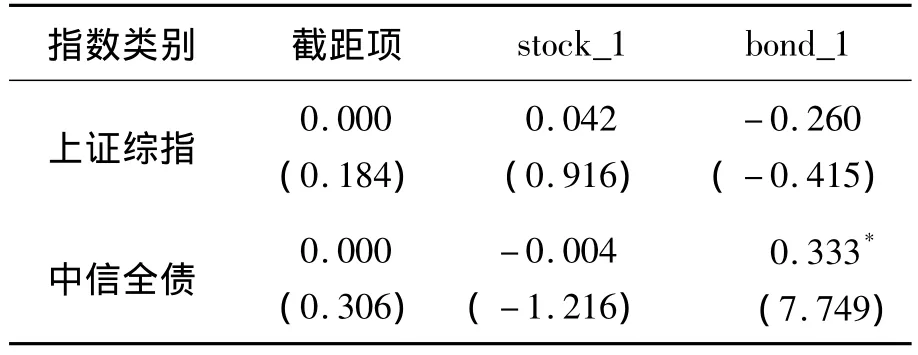
表2 单状态VAR模型估计结果Table 2 Estimation Results of Single State VAR Model

由表3可知，在机制1，股票超额收益率为负而债券为正;在机制2，股票超额收益率为正而债券为负。在机制1，股票市场的波动率为0.050，债券市场的波动率为0.005;在机制2，股票市场的波动率为0.032，债券市场的波动率为0.002。机制1是高波动状态，机制2是低波动状态。因此，机制1对应通常所说的熊市，机制2对应牛市。在不同机制下，股票和债券都负相关，相关系数非常小，几乎为0。在两种机制下，债券的滞后一阶系数均显著，与债券存在序列自相关相吻合，在机制2股票的滞后一阶系数显著。由转移矩阵可以算出稳定状态概率为(0.195，0.805)。从Panel E的估计结果可以看出，当前处于熊市下一期仍处于熊市的概率为0.844，熊市状态的平均持续期为6.420周;当前处于牛市下一期仍处于牛市的概率为0.962，牛市状态的平均持续期为26.520周。牛市的持续期要明显高于熊市，当前处于熊市下一期处于牛市的概率大于当前处于牛市下一期处于熊市的概率。

图1为熊市和牛市的平滑概率，可以看出它们是完全相反的。从图1可以看出，2006年之前中国股市在牛市和熊市之间交替转变，每种状态持续的时间都相对较短。之后中国股市进入较长的牛市，时间从2006年1月至2007年12月，次贷危机的影响逐渐显现出来，直到2009年4月股市才开始慢慢回暖。

4 最优投资组合模型

4.1 基本模型

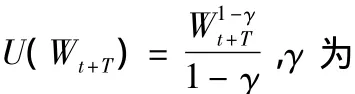
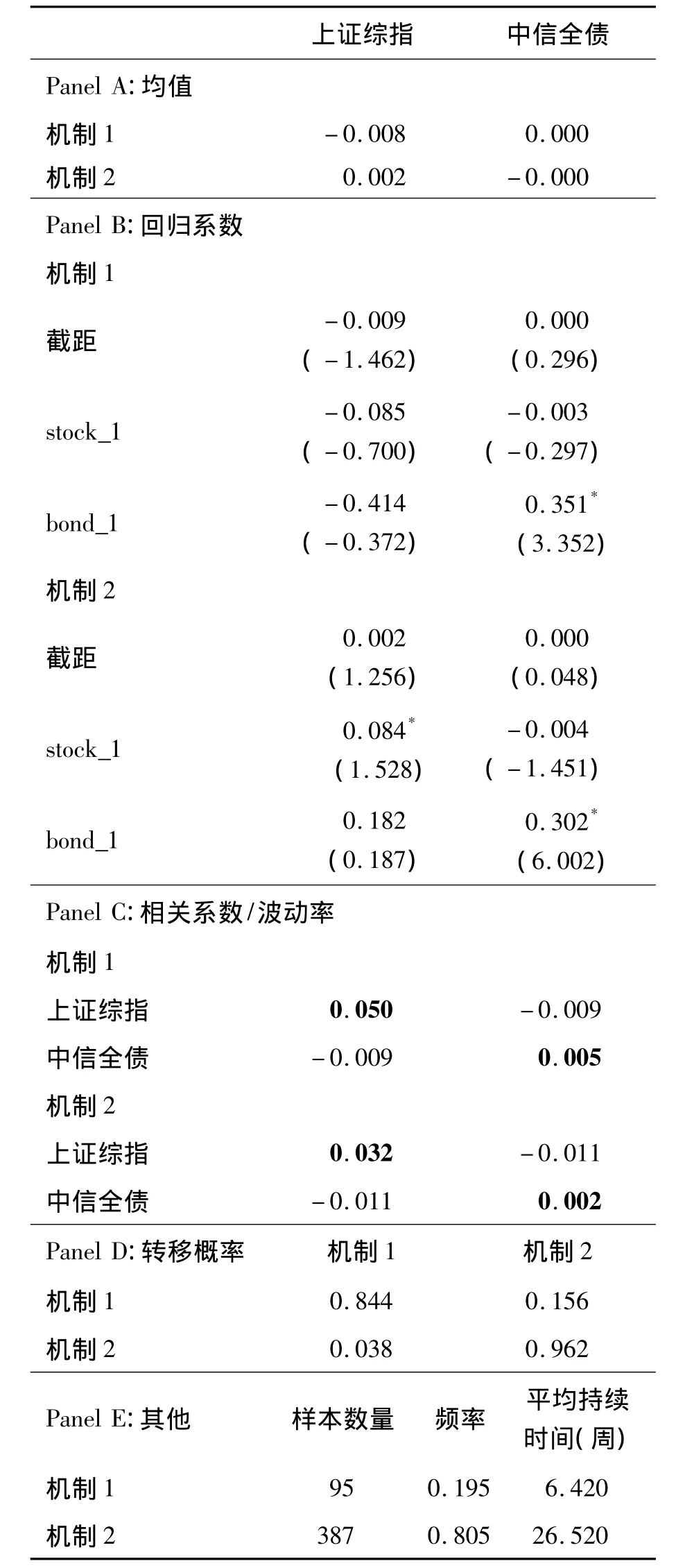
表3 MS(2)-VAR(1)模型参数估计结果Table 3 Parameter Estimation Results of MS(2)-VAR(1)Model

一个购买并持有的投资者通过最大化期末期望效用确定t时刻的投资权重，即

其中，Et为基于t时刻信息集的条件期望，exp()为指数函数，rt:t+T为从期初t时刻到期末(t+T)时刻风险资产的累积超额收益率，rt+τ为(t+τ)时刻风险资产的超额收益率，τ=1，2，…，T。(3)式是单期静态的投资组合选择问题。然而，当交易成本不是太高时，一个理性的投资者可能会根据投资环境的变化适时地调整投资组合头寸，而不是从期初到期末一直持有同一头寸。

令φ为投资者调整组合的频率，tb为投资者第 b次调整组合的时刻，tb=t+b，B为总的调整次数，B=，b=0，1，…，B-1，ωb为tb时刻风险资产的权重，(1-ι2ωb)为tb时刻投资于无风险资产的权重。

其中，Wb为第b次调整时投资者所拥有的财富。

当B=1、φ=T时，(4)式就简化为(3)式，即购买并持有策略。采用动态最优化方法求解(4)式最优化问题，(4)式的价值函数为

b为转移概率矩阵;zb为tb时刻的状态概率向量，其中第一个元素表示当前市场处于熊市的概率，第二个元素表示当前市场处于牛市的概率。由于信息不对称和投资者自身因素的限制，投资者在当前时点上只能观测到过去和当前的资产价格变动，无法确切地观测到当前的市场状态(究竟是牛市还是熊市)。随着时间的推移，投资者根据新获得的信息更新其对市场状态的认识，继而调整他们的组合头寸，使动态资产组合处于最优状态。投资者的这种学习行为对投资组合选择非常重要，因为投资组合选择不仅依赖于预期的资产收益，还依赖于投资者对市场处于何种状态的认识。假设投资者根据贝叶斯学习准则更新他们对当前市场状态的判断，下一时刻的状态概率为

在幂效用函数下，价值函数为

由于(10)式最优化问题难于求出解析解，因此采用 Guidolin等［9］介绍的蒙特卡罗方法模拟计算预期效用，再用动态最优化的倒推法求得 t时刻的权重，假设模拟次数为M。

算法思路如下。

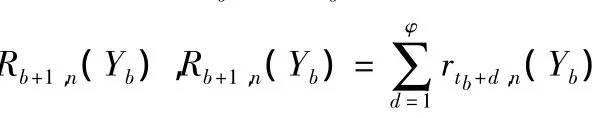
其中，α'j为二维行向量，第 q个元素为1，其他元素为0。

(2)投资者更新下一时刻的信念

(3)重复步骤(1)到步骤(2)，得到一系列的zb和Rb+1，n(zb，n)。

(4)用倒推法计算每一时刻的权重

初始条件为Q(zB，tB)=1。

在购买并持有策略下，不用执行步骤(2)～步骤(4)，最优化问题简化为

4.2 实证结果

传统金融理论在资产收益率独立同分布的假设下，认为投资者的投资决策只与风险厌恶水平等因素相关，而与投资期限无关，即长期投资者与短期投资者的资产组合完全相同，投资者存在短视效应。Campbell等［23］在资产对数收益率服从独立同分布(记为IID)的条件正态分布、投资者最大化期末幂效用假设下得出最优风险资产的投资权重为，，Et为基于t时刻信息集的条件期望，rζ，t+1为第 i个风险资产的对数收益率，为 第 i个风险资产的对数收益率的方差。

利用本研究的样本数据，运用Matlab编程，进行50 000次模拟，得到在风险厌恶水平为5时单状态独立同分布情况下最优股票权重为0.136，最优债券权重为0.864。

假设风险厌恶水平为5，t时刻的市场状态分别为熊市、牛市和稳定状态，即zt=(1，0)'、zt=(0，1)'，zt=(0.195，0.805)'，购买并持有策略的最优决策如图 2所示，横坐标表示投资期限，单位为月。从图2可以看出，投资者对当前市场状态的判断是影响其短期(投资期限1年以下)投资决策的关键因素，短期期限效应非常明显。投资期限越长，人们对股票的投资越谨慎，债券投资的比重加大，权重稳定在某个固定水平，而且任一种状态下的股票投资权重都会大于IID的情形。

当t时刻市场状态是熊市时，在短期内投资者不投资股票，随着时间的推移，他们相信市场会慢慢变好，股票投资的权重慢慢增加，债券的情形正好相反。当t时刻市场状态是牛市时，短期内投资者将40%的财富投资于股票，随着时间推移，减持股票，增加对债券的投资。当t时刻市场状态为稳定状态时，投资决策非常类似于IID的情形，股票投资权重稳定在20%左右，债券投资权重稳定在80%左右，也就是说当投资者无法确定当前的市场状态时他们就采取某种稳定的投资策略，不管投资期限有多长。稳定状态下，股票的投资权重比IID情形下的投资权重大，这是由于市场状态不确定性使投资者产生对冲这种不确定性的规避需求，二者的差距就是对冲组合。另外还发现股票和债券的决策是互补的，即使在熊市时投资者也不投资于无风险资产，这可能是因为中国股、债市场的相关性几乎为0，不管初始状态如何，债券都能够很好地分散风险。

很显然，最优决策与风险厌恶水平密切相关。图3描绘了熊市和牛市情形下风险厌恶水平对投资决策的影响，假设风险厌恶系数取值为从2到20，对投资期限为1个月(短期)和10年(长期)两种情况进行对比。从图3可以看出，在短期，当状态为熊市时，不管是低风险厌恶还是高风险厌恶的投资者都选择不投资股票，而是将全部财富投资于债券;状态为牛市时，低风险厌恶的投资者只投资股票，随着风险厌恶水平的增加，股票投资权重逐渐减少。当投资期限长达10年时，牛、熊市的股票投资权重是风险厌恶系数的减函数，并且在同一风险厌恶水平下，牛、熊市的股票投资权重几乎一致(在图3中表现为两线基本重合)。这意味着，当投资期限很长时，市场状态的变化对投资者的投资决策没有影响，投资者按略高于IID情形下的权重进行股票投资。另外，本研究发现风险厌恶水平越低，股票投资权重变化趋势比IID情形下变化越快，债券的情形正好相反，这里不再赘述。

下面讨论不同的市场状态和投资者学习行为对投资者投资决策的影响。表4给出风险厌恶水平为5、不同投资期限、不同的组合调整频率下的投资权重。当φ＞T时用NA表示。从表4可以看出，在熊市，不管调整频率多大，投资者都选择不投资股票，全部投资于债券，而且动态调整的期初股票头寸都比购买并持有策略以及IID情形下的股票头寸小，说明在熊市，投资者学习行为使投资者更为谨慎。在牛市，投资者将30%的财富投资于股票，70%的财富投资于债券，动态调整的期初股票头寸都大于购买并持有策略以及IID情形下的股票头寸，说明当市场向好时，投资者学习行为导致投资者投资于更多的风险资产。另外，在牛市，短期投资者的期初股票头寸对动态调整频率的反应比长期投资者更为敏感。在稳定状态，投资者几乎将全部财富投资于债券，而且稳定状态的期初股票头寸都小于购买并持有策略及IID情形下的股票头寸。因为在稳定状态情形下，投资者无法确定当前的市场状态，即使可以通过不断地学习重新判断市场状态，但在期初他们对股票的投资是谨慎的。另外，直觉上，φ越小，投资者可以学习的信息就越少，投资者对市场状态的变化就应更为敏感，所以在同一期限内，φ越小，期初股票头寸应该更少。但本研究发现，在同一期限，在牛市对应不同的调整频率，期初的头寸基本没有变化，都比较稳定;而在稳定状态，φ越小，期初的股票头寸越大，这说明虽然动态调整头寸的频率越长，可供学习的信息越多，但未来的不确定性也越大，投资者的投资行为越为谨慎。由于债券情形与股票相反，这里就不再赘述。

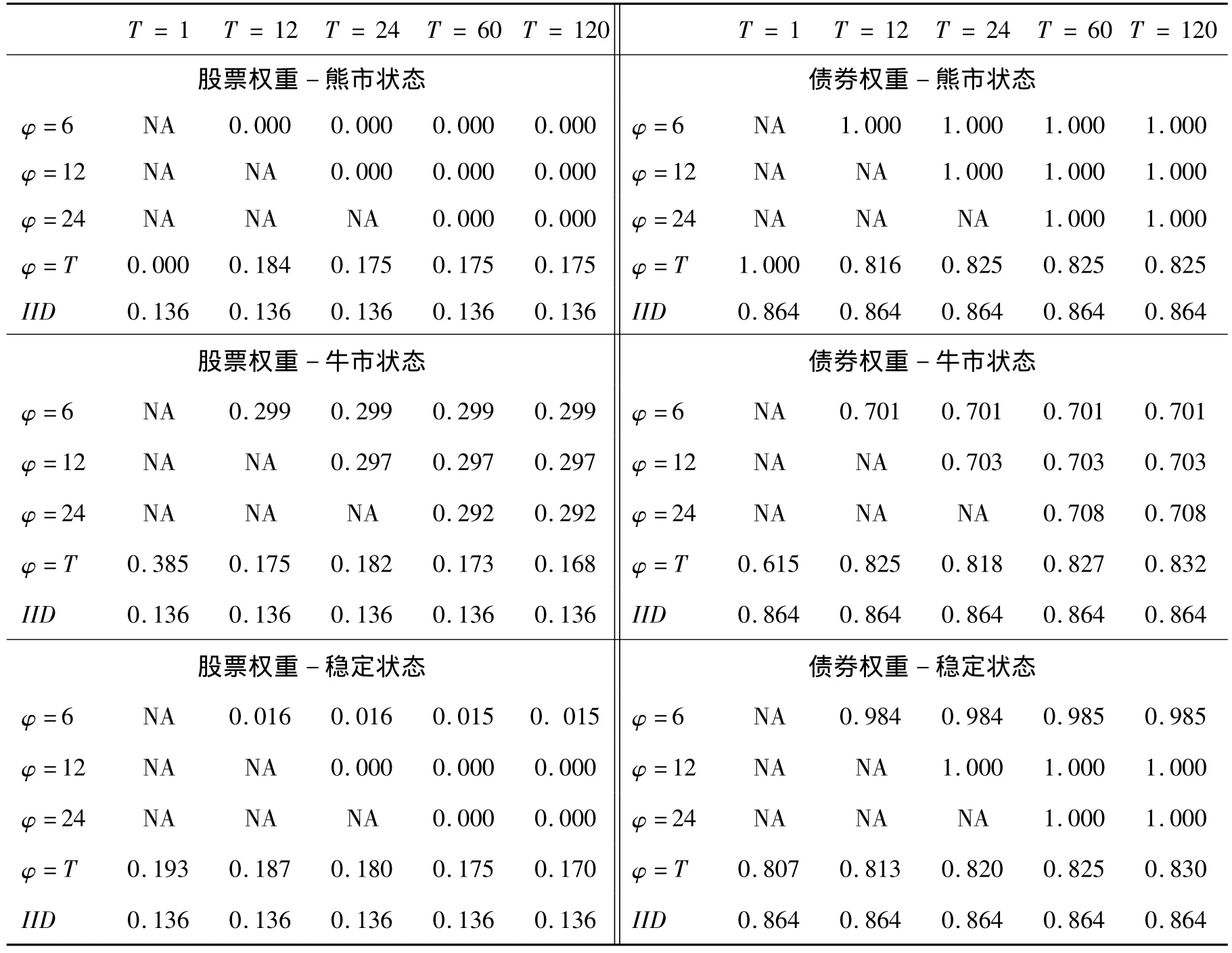
表4 动态调整对最优投资权重的影响Table 4 Impact of Dynamic Adjustment on Optimal Portfolio Weights

实证分析表明，不同的市场状态对最优投资组合选择有很大的影响，这是否意味着投资者的效用可以得到提高。本研究采用效用成本的概念对单状态资产配置与不同市场状态资产配置模型的期望效用进行对比，为了度量效用成本，先计算初始财富的增加或者补偿，即投资者为了得到与机制转换模型下相同的期望效用而提供的初始财富的补偿。这里只比较稳态概率的情形。

效用成本是风险厌恶系数的函数，一般来说，风险厌恶水平越高，效用成本越低。因此，本研究讨论风险厌恶系数为10这种极端情况下的效用成本。图4为效用成本随投资期限的变化趋势图，由图4可知，在极度风险厌恶情形下，效用成本从1个月期的1.8%变动到10年期的1.2%，说明考虑不同市场状态的投资组合能够提高投资者效用。

5 结论

本研究放松传统模型中参数不变的假设，引入投资者学习行为，研究状态变化和投资者学习行为下的最优资产选择问题，对传统模型进行补充。研究结果表明，中国股票市场和债券市场存在明显的结构变化特征，可以将资本市场分成高波动负收益(熊市)和低波动正收益(牛市)，而市场状态的转换对最优资产选择的影响是显著的。有别于传统的投资组合选择模型，市场状态变化下的投资组合选择模型存在较大差别。

在购买并持有情形下，不同的市场状态投资者采取不同的投资策略。在短期内，当市场处于熊市时投资者将全部财富投资于债券，不投资于股票;牛市时股票的投资比重大大增加，占投资者财富的40%左右。随着投资期限变长，牛、熊市下的投资权重稳定在某个水平。当投资者无法确定当前市场处于何种状态时，他们就采取某种稳定的投资策略，同时市场状态的不确定性造成投资者产生对冲这种状态不确定性风险的需求。

动态投资组合模型表明，投资者的学习行为影响人们的投资决策。当市场向好时，投资者学习行为导致其投资于更多的股票资产;当市场状态无法确定时，学习行为使投资者对股票的投资更为谨慎。但在同一期限内，在各种状态下调整频率的高低对期初持有头寸没有太大的影响。

本研究突出了非对称的市场状态以及投资者学习行为在资产组合选择过程中的重要性，为中国投资者(特别是保险公司、社保基金和企业年金等长期投资者)提供了有价值的参考。但本研究是直接从资产价格的数据生成过程中“挖掘”出不同的市场状态，并在此基础上研究最优投资组合选择行为，这个假定使模型具有一定的局限性。由于资产价格受各种因素影响，特别是宏观基本面消息，因此更为现实的方法是将宏观经济因素加入模型，结合宏观经济波动和股票价格区别不同的市场状态，进而研究不同的市场状态下的最优投资组合选择行为。

［1］Longin F，Solnik B.Extreme correlation of international equity markets［J］.The Journal of Finance，2001，56(2):649-676.

［2］Ang A，Chen J.Asymmetric correlations of equity portfolios［J］.Journal of Financial Economics，2002，63(3):443-494.

［3］刘琛.相关性风险价格:中国股市的证据［D］.厦门:厦门大学，2010:20-24.

Liu Chen.The price of correlation risk:Evidence from Chinese stock market［D］.Xiamen:Xiamen U-niversity，2010:20-24.(in Chinese)

［4］Pastor L，Veronesi P.Learning in financial markets［J］.Annual Review of Financial Economics，2009，1(1):361-381.

［5］Ang A，Bekaert G.International asset allocation with regime shifts［J］.The Review of Financial Studies，2002，15(4):1137-1187.

［6］Ang A，Bekaert G.How regimes affect asset allocation［J］.Financial Analysts Journal，2004，60(2):86-99.

［7］Liow K H，Zhu H.Regime switching and asset allocation:Evidence from international real estate security markets［J］.Journal of Property Investment＆ Finance，2007，25(3):274-288.

［8］Guidolin M，Timmermann A.Economic implications of bull and bear regimes in UK stock and bond returns［J］.The Economic Journal，2005，115(500):111-143.

［9］Guidolin M，Timmermann A.Asset allocation under multivariate regime switching［J］.Journal of Economic Dynamics and Control，2007，31(11):3503-3544.

［10］Guidolin M，Timmermann A.Size and value anomalies under regime shifts［J］.Journal of Financial E-conometrics，2008，6(1):1-48.

［11］Guidolin M，Timmermann A.International asset allocation under regime switching，skew，and kurtosis preferences［J］.The Review of Financial Studies，2008，21(2):889-935.

［12］Tu J.Is Regime Switching in Stock Returns Important in Portfolio Decisions?［J］.Management Science，2010，56(7):1198-1215.

［13］李卓，赵勇.风险的多态性与投资组合构造:一种基于Markov状态更替的 CAPM模型［J］.世界经济，2005，28(7):60-68.

Li Zhuo，Zhao Yong.Polymorphism of market risk and portfolio selection［J］.The Journal of World E-conomy，2005，28(7):60-68.(in Chinese)

［14］苏涛，詹原瑞，刘家鹏.基于马尔科夫状态转换下的CAPM实证研究［J］.系统工程理论与实践，2007，27(6):21-26.

Su Tao，Zhan Yuanrui，Liu Jiapeng.The empirical research of CAPM based on Markov regime switching［J］.Systems Engineering-Theory ＆ Practice，2007，27(6):21-26.(in Chinese)

［15］赵鹏，唐齐鸣.Markov区制转换模型在行业CAPM分析中的应用［J］.数量经济技术经济研究，2008，25(10):87-97.

Zhao Peng，Tang Qiming.The application of Markov regime switching model in industrial CAPM analysis［J］.The Journal of Quantitative ＆ Technical Economics，2008，25(10):87-97.(in Chinese)

［16］Hoeting J A，Madigan D，Raftery A E，Volinsky C T.Bayesian model averaging:A tutorial［J］.Statistical Science，1999，14(4):382-417.

［17］Wachter J A.Asset allocation［J］.Annual Review of Financial Economics，2010，2(1):175-206.

［18］孟卫东，何朝林.基于学习行为的动态资产组合选择［J］.系统工程理论与实践，2007，27(9):38-46.

Meng Weidong，He Chaolin.The choice of dynamic portfolio based on the learning behavior［J］.Systems Engineering-Theory ＆ Practice，2007，27(9):38-46.(in Chinese)

［19］杨朝军，陈浩武.参数不确定性对投资者最优资产组合的影响:基于中国的实证［J］.中国管理科学，2008，16(3):37-43.

Yang Chaojun，Chen Haowu.Parameter uncertainty and investor's portfolio choice:Evidence from China stock market［J］.Chinese Journal of Management Science，2008，16(3):37-43.(in Chinese)

［20］Honda T.Optimal portfolio choice for unobservable and regime-switching mean returns［J］.Journal of Economic Dynamics and Control，2003，28(1):45-78.

［21］Hamilton J D.Time series analysis［M］.Princeton:Princeton University Press，1994:690-700.

［22］Krolzig H M.Markov-switching vector autoregressions:Modelling，statistical inference，and application to business cycle analysis［M］.Berlin:Springer，1997:47-57.

［23］Campbell J Y，Viceira L M.Strategic asset allocation:Portfolio choice for long-term investors［M］.2nd ed.New York:Oxford University Press，2002:22-25.

Funded Project:Supported by the Youth Foundation of Southwest University of Political Science＆Law(2011-XZQN23)

Biography:Dr.Chen Zhiying，a Fujian Putian native(1983-)，graduated from Xiamen University and is a lecturer in the School of Economics at Southwest University of Political Science＆ Law.Her research interests include asset pricing and finance engineering，etc.

E-mail:zhi_ying_chen@163.com

Optimal Portfolio Choice under Regime-switching and Learning Behaviors

Chen Zhiying
School of Economics，Southwest University of Political Science＆ Law，Chongqing 401120，China

Aiming at the nonlinear dynamic change of the financial asset return series and the traditional assumption of investor parameter certainty，the research explores the optimal portfolio choice under regime-switching and the impact of investors'learning behaviors under parameter uncertainty on the optimal portfolio choice.We use Markov regime-switching model to depict changes of market states，adopt the Bayesian learning rule to describe investors'learning behaviors，build the discrete model of optimal portfolio choice under regime-switching and learning behaviors，utilize the expectation maximization algorithm and dynamic optimization method to estimate the model parameters and make use of the Monte Carlo method to simulate investors'portfolio choice behaviors.The research shows that there are significant structural dynamic changes in Chinese financial market，which can be divided into bull and bear markets.In the short term，investors do not lay any wealth in stock but bonds when the market is in a bear market，while the proportion of stock investment will magnificently increase when the market is in a bull market.In the long term，weight of stocks and bonds in bull and bear states will stabilize at a certain level.Meanwhile，the uncertainty of market states induces investors'hedging demand of the uncertainty risk.In the bull state，investors'learning behaviors drive them to invest more in risky assets;in the unstable state，investors is more cautious on stock.Portfolio choice under regimeswitching improves the overall utility of investors.

optimal portfolio choice;regime-switching;bear market and bull market;Bayesian learning;utility cost

Date:June 15th，2012 Accepted Date:September 24th，2012

F830

A

10.3969/j.issn.1672-0334.2013.02.008

1672-0334(2013)02-0081-09

2012-06-15 修返日期:2012-09-24

西南政法大学校级青年项目(2011-XZQN23)

陈志英(1983-)，女，福建莆田人，毕业于厦门大学，获博士学位，现为西南政法大学经济学院讲师，研究方向:资产定价和金融工程等。E-mail:zhi_ying_chen@163.com