薄壁直圆柱管质量流量的测量与特性分析

李 兵，魏玉兰

（湖州师范学院 信息与工程学院，湖州 313000）

0 引言

随着科学技术的不断发展，大量的薄壁直圆柱管被广泛应用于航天、航空、船舶、石油等工业部门，比如连接油田和炼油厂、运油港口的输油管道[1～3]。圆柱管内的液体对管道的固有频率产生一定影响。一方面，人们利用固有频率设计了应用于输油、输气的管路圆柱管，通过改变影响固有频率的因素以使圆柱管的振动幅度不致过大，以免引起破坏；另一方面，通过圆柱管的振动可获得圆柱管内的流量，从而判断圆柱管内是否堵塞。所以含流体圆柱管的研究有着重要的意义。Fuller和Fahy[4]利用流固耦合理论，建立了充液圆柱壳的自由振动方程。此外，在理论上对含流体圆柱管道的振动特性、非线性振动、质量流量测量等方面进行了研究[5～7]。但对薄壁圆柱管的质量流量测量与振动特性的实验研究较少，本文以两端固支含流动液体薄壁直圆柱管为实验结构，并简化为Timoshenko梁模型，在外加激振的情况下，分析科氏力对圆柱管振动的影响，并通过自行搭建的实验装置，确定圆柱管内流体的质量流量和振动特性，并对误差进行分析。

1 基本理论

流体在薄壁圆柱直管内流动会产生科里奥利加速度，管道内的质量流量可通过分析该加速度所产生的科氏力对管道振动的影响而确定。在一根两端固定的管道中间，施加一激振力，如图1所示。在流速为零时，对以中点为基准的对称点来说会产生同向振动。当液体流动时，由于科氏力的作用，管道前半段振动受阻尼影响，振动角速度减少，而后半段振动角速度增大。这样，两侧对称点就不再是同相振动，而存在一转角差。这个转角差与要获得的质量流量成正比。

图1 实验台

当管中无液体或流速v=0时，管上任一点位移曲线为[8～10]：

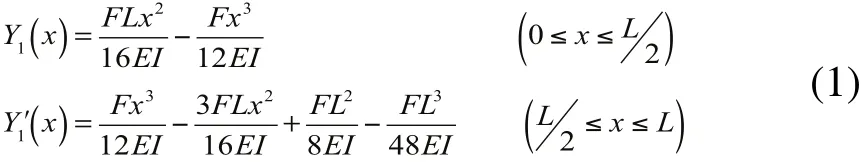
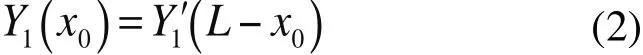
当管中有流速为 的流体流动时，管子除受到激振力F作用，还受到附加科氏力的作用，如图2所示。设(02)，可得科氏力载荷积度：

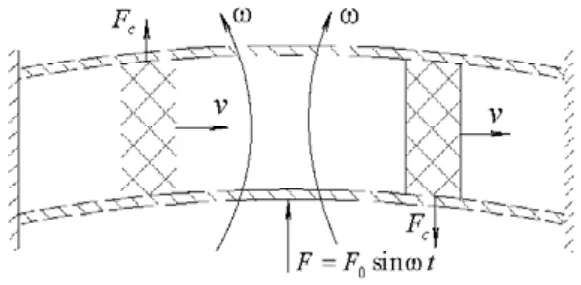
图2 直圆柱管变形曲线

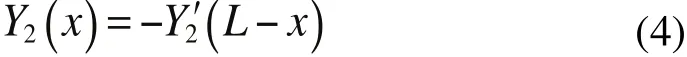
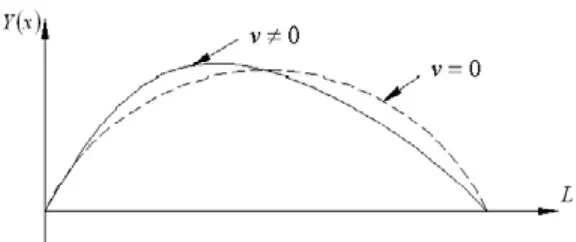
图3 位移变化图

当管内液体流动时，在激振力作用下，两对称点x0及L x0处位移分别为：

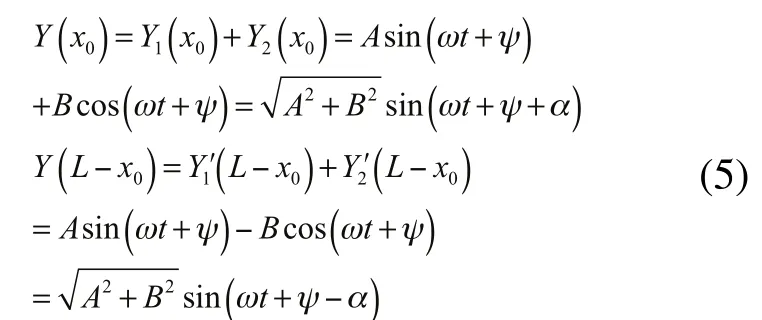
式中，

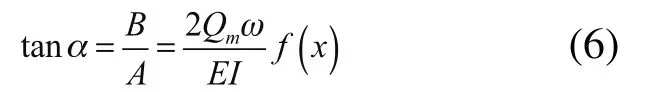
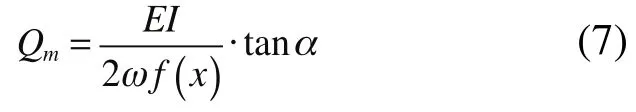
在测量时，通过分析圆柱管两对称点处振动响应信号间的转角差即可获得角，从而可计算出单位时间内流过管道的质量流量，通过换算，可获得其流速。

2 实验装置与方法

2.1 实验装置

实验装置被固定在一个平台上以保证其良好的稳定性。薄壁直圆柱管采用两端固定式的约束方式。为了保证激振的均运性，激振器被安装在圆柱管的中点处。在圆柱管上均匀分布6个应变片式传感器，而且这些传感器以激振器为中心对称安装在直圆柱管上部[11]。实验装置如图4所示。

图4 实验装置

整个系统装置可分为两大部分：激振系统和数据采集处理系统[3]。激振系统采用2Kg的电磁激振器和Agilent 33220A函数/任意波形发生器。数据采集处理系统使用YE7600数据采集系统和YE7600 Dynamic data acquisition & analysis system数据采集分析软件。

2.2 实验方法

为了获得薄壁圆柱管内的质量流量，需要先分别获得液体静止和流动时圆柱管的振动响应曲线，并获得幅频特性曲线，分析两组响应曲线可获得转角差，根据方程(8)计算可获得薄壁直圆柱管内的质量流量。由于圆柱管上的应变片传感器不能绝对对称安装，在圆柱管对称位置上的两个传感器获得的振动响应不能完全重合，会有一定的转角差，所以在测量流动液体的质量流量时也要虑进该转角差，才能得到准确的质量流量。

3 实验分析

3.1 振型与固有频率

为了获得准确的转角差，需要获得液体静止和流动时薄壁直圆柱管的振动响应和固有频率。流经薄壁圆柱管的实际流量选为39Kg/min，压力为0.02106N/m2，薄壁圆柱管含静止液体和含流动液体的一阶振动响应曲线如图5和图6所示[3]。

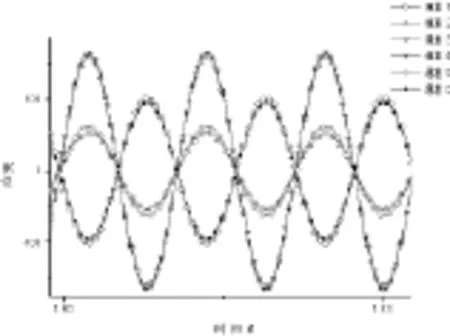
图5 流量为零时一阶响应曲线

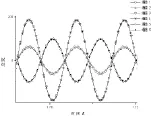
图6 流量为39Kg/min时一阶响应曲线

由图5和图6，分析同一时刻圆柱管上的振动响应曲线，可获得圆柱管含静止液体和含流动液体的一阶幅频特性曲线[11,12]，如图7和图8所示。为消除激振力幅值对幅频特性曲线的影响，应把各点的应变除以激振力的最大平均值。分析前三阶振动响应曲线，可获得不同流量时圆柱管振动的固有频率和模态阻尼比，如表1和表2所示。

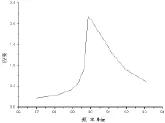
图7 流量为零时一阶幅频特性曲线

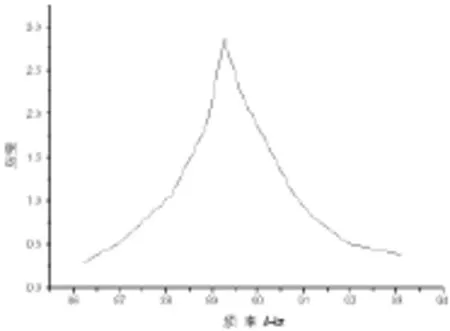
图8 流量为39Kg/min时一阶幅频特性曲线

从表1和表2可看出，薄壁直圆柱管内液体的流量影响其固有频率，既流量增大时固有频率减小，流量减小时固有频率增大，在圆柱管各处截面相同的情况下，流量大代表着流速大。则液体的流速影响圆柱管的固有频率，即流速增大时固有频率减小，流速减小时固有频率增大。

3.2 质量流量测量

由于圆柱管上布置的应变片传感器并不能达到完全对称安装，在计算转角差时需要考虑液体静止时圆柱管对称位置振动的转角差，所以在做质量流量实验时要先做液体流动的实验，然后在不改变激振频率和激振力的情况下，快速把两端阀门关上并把水泵关上，之后作含静止液体的实验。这样才能获得比较准确地响应信号。信号的记录方法和分析方法与前面的实验相同。选用一阶振动进行分析，因为一阶振动比较容易激振，科氏力对一阶振动也影响最大，由于二阶振动时不能在中点激振，导致振动响应信号不对称。在本系统中选用了2号和5号两个对称点的应变片传感器进行分析计算，2号传感器位于左端面163mm处，2,5为2号和5号应变片传感器处振动响应的转角差。分别选用不同的激振频率和激振力，而且选用两种流量进行分析计算，如表3和表4所示。

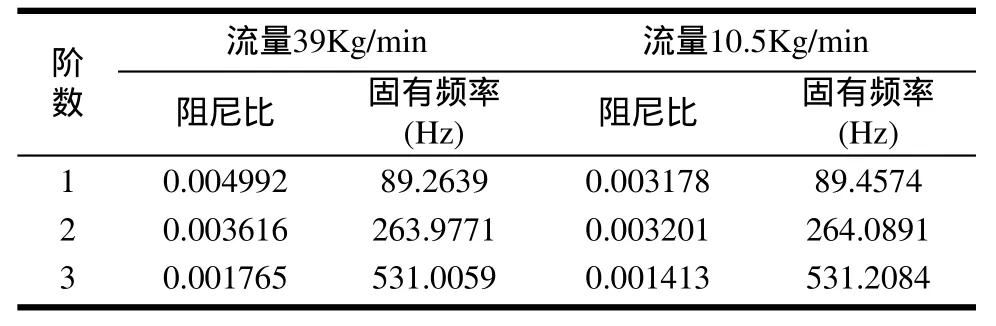
表1 不同流量时的阻尼比和固有频率

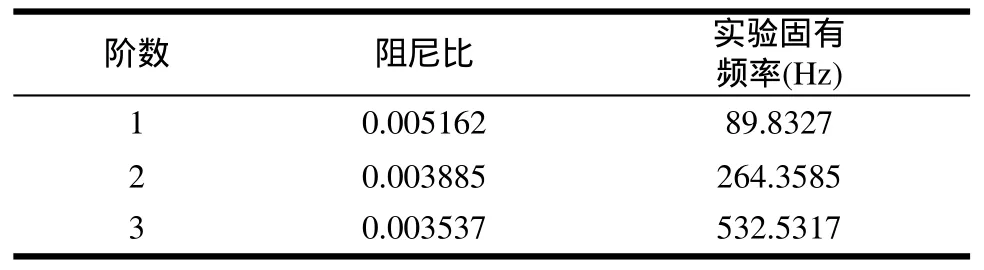
表2 流量等于零时的阻尼比和固有频率

从表3和表4中可看出，使用该种方法获得的质量流量与实际值接近，但在共振点处的测量值与实际值偏差较大。

通过实验获得的流量与实际流量存在误差。这是由于被测圆柱管的直径、壁厚不均匀和圆柱管本身有焊缝造成圆柱管的几何特性变化，此外为了密封在两固定端都使用了橡胶垫片，这样使系统的约束方式不能达到完全固定，影响其约束方式，测量仪器的精度不高也造成了误差。

在共振点时实验得到的流量与实际流量有很大误差且无规律。这是由于实验采用的应变片传感器无法完全对称安装，要考虑液体静止时对称点的转角差。当选用流体流动时的共振频率点进行实验时，由于此时系统处于共振状态，无法获得准确的转角差，所以实验获得的流量与实际流量相差较大，同理在选用液体静止时的共振频率点计算流量时，也存在较大误差。相反，其它频率点都不是共振点，在这些频率点下进行测量，可得到比较准确的流量。所以在测量流量的时候应避免共振点。

4 结论

根据含流体薄壁直圆柱管的振动特性，可以测量管内的质量流量。介绍了理论计算方法和实验装置。通过实验与分析获得了薄壁直圆柱管含流动液体情况下的振动响应、振型、固有频率和幅频特性性曲线。获得以下结论：

1）圆柱管内液体的流速会影响其固有频率，当流速增大时固有频率减小，流速减小时固有频率增大。

2）通过实验与计算可获得圆柱管内含流动水时的质量流量，其实验值与实际值较接近。

3）在非共振频率点时，实验得到的质量流量与实际的质量流量相接近；相反，在共振频率点时实验获得的质量流量与实际值相差较大且无规律。

4）造成质量流量实验误差的原因：应变片传感器无法完全对称安装，需考虑液体静止时的转角差，在测量质量流量的时候应该避免液体静止和流动时的共振点，在非共振点测量，可以得到比较准确的质量流量。

表3 实际流量为10.5Kg/min

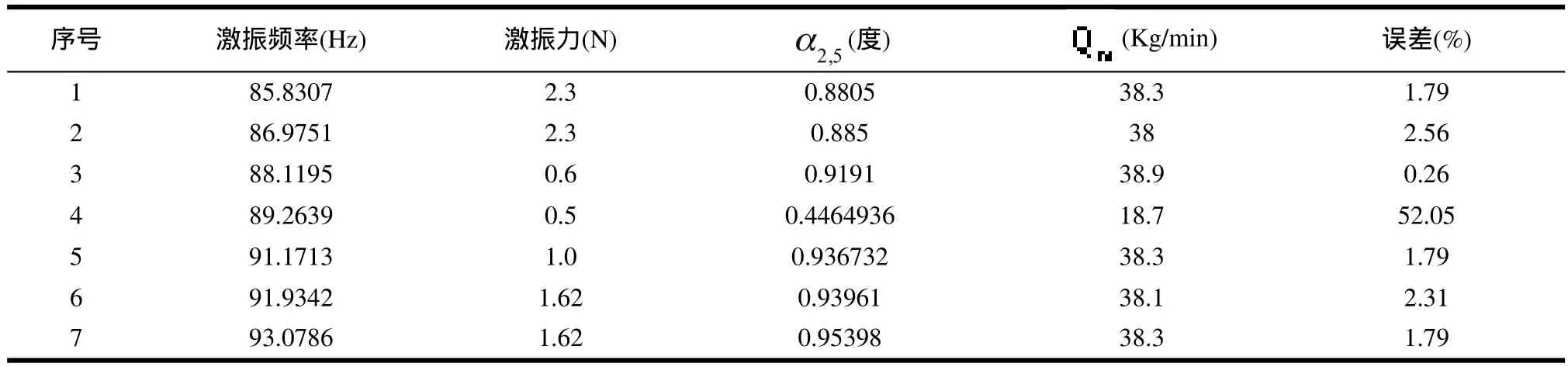
表4 实际流量为39Kg/min

[1] ALDRAIHEM O. J. Analysis of the dynamic stability of collar-stiffened pipes conveying fl uid [J]. Journal of Sound and Vibration,2007,300(1):453-465.

[2] Panda L.N. and Kar R. C.Nonlinear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances[J].Journal of Sound and Vibration,2008,309(3):375-406.

[3] 李兵,谢里阳,郭星辉,等.流体对薄壁圆柱管振动频率的影响[J]. 振动与冲击,2010,7:193-195.

[4] Fuller C.R.and Fahy F.J.Characteristics of wave propagation and energy distributions in cylindrical elastic Shells fi lled with fl uid[J].Journal of Sound and Vibration,1982,81(4):501-518.

[5] Kutin J. and Bajsic I.Characteristics of the shell-type Coriolis flowmeter [J].Journal of Sound and Vibration,1999,228(2):227-242.

[6] 宋明刚,樊尚春.非线性对Coriolis质量流量测量管振动特性影响的理论研究[J].仪器仪表学报,2002,23(4):361-365.

[7] Amabili M.,Pellicano F. and Paydoussis M. P. Nonlinear dynamics and stability of circular cylindrical shells containing flowing fluid [J].Journal of Sound and Vibration,2000,237(4):617-640.

[8] 吴福光,蔡承武,徐兆,等.振动理论[M].北京:高等教育出版社,1987.

[9] 汪克文,朱超平,周一届,等.直管科氏质量流量计传感器理论设计 [J].自动化与仪器仪表,2000,3:47-49.

[10] 杨俊,陈明.直管式科氏质量流量计最佳测量点分析[J].航空计测技术,2003,23(4): 5-8.

[11] 李兵,郭星辉,谢里阳,等.直管科里奥利质量流量计的测量方法与实验[C]//全国压电和声波理论及器件技术研讨会,武汉,2009,257-261.

[12] 倪伟.科里奥利质量流量计的信号处理方法的研究[J].测试技术,2004,3:6-9.