基于粒子群优化及多结构估计的ASIFT特征提取算法

曹雪莲，陈水利

(1．福州大学数学与计算机科学学院，福建 福州 350108;2．集美大学理学院，福建 厦门 361021)

0 引言

图像特征提取是图像分析、模式识别以及机器视觉等领域的研究热点．理想的图像局部特征能表达图像局部区域的信息，对视角变化、光照变化、尺度缩放、旋转等情况具有不变性．局部特征的研究成果已经被广泛应用于宽基线特征匹配[1]、物体识别[2]、纹理识别[3]、图像检索[4]、机器人定位[5]、视频数据挖掘[6]、全景图像拼接[7]等领域．

一些经典的特征检测子，如Harris角点检测子[8]可以对图像旋转保持不变性，Harris－Laplace和Hessian－Laplace检测子[9]可以对图像旋转和尺度缩放保持不变性．而Harris－Affine和Hessian－Affine检测子[9]，MSER(最大稳定极值)检测子[10]等都是为解决仿射不变性而提出的．2005年，Mikola-jczky[11]对SIFT、GLOH、PCA－SIFT等10种不同的特征描述子从尺度缩放、视角变换、光照变化等6个方面进行了实验和性能比较，结果表明，SIFT性能最好、最稳定．2009年，Jean－Michel Morel等[12]提出了ASIFT(Affine－SIFT)算法，在SIFT算法的基础上，解决了仿射不变性问题．ASIFT算法通过离散采样搜索图像之间的最优变换模型，而实际上ASIFT中两个旋转角度参数是连续的，通过离散采样得到的解一般不是实际的最优采样角度．

虽然上述算法能够得到大量的特征匹配点对，但是不可避免会存在很多错误的匹配对．如何解决特征错配，正确估计图像变换参数及多结构估计是本文的重要目标．特征去错配与结构估计可以转化为模型拟合问题，即在噪音数据中提取特征的变换模型 (结构)．常用的模型拟合方法包括最小二乘法[13]、Hough变换[14]、RANSAC[15]等．最小二乘法是以残差平方和最小的原则作为直线参数估计结果，但是当存在严重噪声时，该方法将不能正确估计模型．Hough变换利用点与线的对偶性，将原始图像空间给定的曲线通过曲线表达形式变为参数空间中的一个点．该方法的缺点是参数过多而导致组合爆炸．RANSAC方法虽然能够简单而巧妙地去除部分错误匹配对，但是该方法溃点低，无法实现多结构提取．另外，RANSAC需要明确inliers的尺度，而这往往需要先验知识，因而在许多领域中并不可行．要解决特征去错配，正确估计图像的变换模型，就要实现多结构提取．目前多结构估计的方法有很多，包括 PROSAC[16－17]、ITKSF[18－19]及 Multi-GS[20]等．

因此，本文拟首先用粒子群优化算法 (Particle Swarm Optimization，PSO)对ASIFT的采样进行优化，使参数在更广阔的连续空间中搜索最优解，然后得到更大量的特征匹配对，再用Multi-GS方法对PSO优化后的ASIFT算法的匹配结果进行多结构估计，去除错误的匹配点对，以期最终提取出尽可能多而且精准的匹配点对．

1 ASIFT算法原理

1.1 ASIFT算法流程

定理1[12]任意的非对称仿射矩阵，若满足其行列式是严格的正值，则都有唯一的分解:

其中，λ〉0，λ2t是矩阵A的行列式，Ri是旋转矩阵，φ∈[0，π]，Tt表示倾斜矩阵，t〉1是绝对倾斜参数．图1是公式 (1)的几何解释．其中，U指被拍摄的平面物体，角度φ和θ分别表示相机光轴的经度和纬度，ψ表示相机的旋转角度，λ是缩放参数．

ASIFT算法的基本流程如下:

1)对每幅待匹配的图像，通过改变相机光轴与正面视图的经度和纬度来仿真所有可能的仿射变换情况．图像先经过φ度旋转，接着通过参数进行倾斜变换．如图2所示．

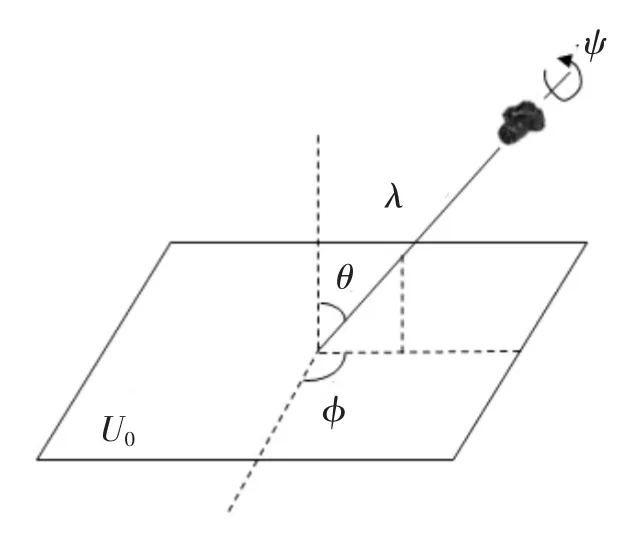
图1 公式(1)的几何解释Fig.1 Geometric interpretation of the Equ.1

2)所有的这些旋转和倾斜变换都是在一个有限的小范围内改变参数φ和θ值得到的，而且，对这些参数的采样步长要确保使不同的φ值和θ值得到的仿射图像之间尽可能相似．对得到的所有仿射图像使用SIFT算法进行特征点提取．

3)对提取完特征点的仿射图像两两之间使用SIFT算法进行匹配，如图2所示．

1.2 粒子群优化的ASIFT算法

粒子群算法的数学描述[21]如下:

设粒子群的种群数量为M，搜索空间为d维，其中第i个粒子在第n次迭代中的位置可以表示为:粒子i的速度为每次迭代中粒子i移动的距离，用表示，则第i个粒子在第n+1代的第j(j=1，2，…，d)维子空间中的速度和位置:

图2 ASIFT算法的概览图Fig.2 Overview of the ASIFT

其中，ω为惯性权值，c1和c2为加速因子，r1和r2是在[0，1]范围内的两个随机数，常量vmax即最大速度用来限制粒子的速度，pij是当前粒子的历史最优位置，gj则表示整个群体的历史最优位置．

本文采用了文献 [22]提出的变异粒子群优化算法，对参数t和φ进行编码．变异粒子群算法中加入了变异因子R，对每一个粒子设置一个随机数ri，在每一次迭代中，若某个粒子的随机数ri的值超过了R的值，则该粒子就发生变异，否则，粒子就进行正常的更新．

粒子群优化的ASIFT算法具体过程如下:

Step1 初始化所有粒子，在允许范围内随机设置每个粒子的初始位置和速度，每个粒子的局部最优解pbest设为其初始位置，全局最优解gbest设为空．

Step2 计算每个粒子的适应值．粒子的编码方式为:

ti1 φi1 ti2 φi2

其中，ti1，ti2分别表示粒子i对应的两幅图像的倾斜参数，φi1，φi2分别表示粒子i的两幅图像的相机光轴的经度，d=4．对应每个粒子的编码值，使用SIFT算法对相应的仿射图像提取特征点，粒子的适应值为对应图像的SIFT匹配数．

Step3 更新每个粒子所经过的最好位置pbest及群体所经历的最好位置gbest．

Step4 检查每个粒子的随机数ri，若ri大于R值，则转Step5，否则，转Step6．

Step5 在允许的范围内随机设置当前粒子的位置．

Step6 根据公式 (2)— (4)更新当前粒子的速度和位置．

Step7 若满足终止条件 (达到最大迭代次数)则终止迭代，否则返回Step2．

2 多结构估计Multi-GS算法

文献[18]提出了Multi-GS多结构估计算法，该算法主要利用有指导的采样来代替随机采样，即利用特征点之间的相似关系来指导采样，由此引入了残差的概念:以透视变换为例，假设输入图像中的一点A(x，y)的对应点坐标为B(x'，y')，而在透视变换模型M的作用下A的实际对应点为A'，因此称理想坐标点B与实际对应点A'的距离r为点A在模型M下的残差．

特征点的相似度函数可以用来指导模型采样，主要采用条件概率的方法选择特征点，从而构造优化的结构．假设 S={xs1，xs2，…，xsp}⊂ χ是构成模型的最小点集，其中，{s1，s2，…，sp}⊂ {1，2，…，N}．随机选择第一个点xs1，而第二个点的选择概率有赖于与第一个点的相似度，相似度越高的点被选中的概率越大:

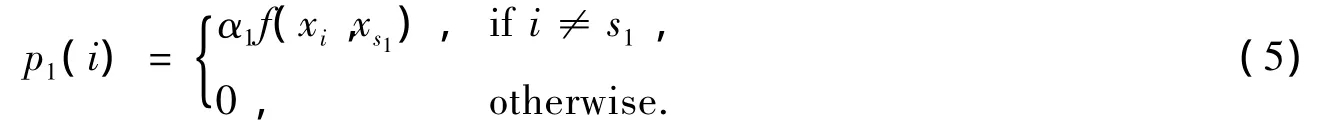
其中，α1是归一化因子，同理，第三个点的选择概率有赖于与第一个点及第二个点的相似度．假设选择每个点是独立的，根据贝叶斯原则，后续点的选择有赖于与被选中点之间的概率乘积，即第k+1个点的选择概率服从:

得到条件概率之后，可以根据统计学原理，通过小样本 (如之前所述的M个)训练得知数据之间的关联 (相似度)，进而根据这类关联引导产生新的样本，新样本将不断添加进模型集合，特征之间的相似度也将不断更新．为了加速算法，每产生k个新模型后再融入模型集M(采用折半插入)．

3 实验结果

3.1 实验设置

PSO优化ASIFT实验以VS 2010作为平台，主要对本文算法与ASIFT算法的匹配结果进行比较．其中，PSO算法种群规模M=10，最大迭代次数为100代．惯性权值ω随迭代次数线性递减，递减公式为ω =ωstart-((ωstart-ωend)×gcrt)/gmax，ωstart和ωend分别为ω的初始值和终止值．gcrt为当前迭代次数，gmax为最大迭代次数．加速因子c1=c2=2，变异参数R随迭代次数线性递减的公式为R=Rstart-((Rstart-Rend)×gcrt)/gmax，Vmax设置为搜索空间的1/6．

Multi-GS算法进行多结构提取的实验以MATLAB7.0为平台，对PSO－ASIFT算法得到的匹配结果进行多结构提取，并与随机采样算法RANSAC的结果做对比．两种算法均设置10 s的CPU运行时间限制．

3.2 实验结果

为了验证本文算法的有效性，采用图3所示的集美大学尚大楼图像进行特征点匹配实验，待匹配图像相对参考图像具有一定程度的尺度和旋转变化．图4分别给出了ASIFT算法和PSO－ASIFT算法的特征匹配结果，其中图4a表示ASIFT算法得到225对匹配点对，图4b表示PSO－ASIFT算法得到471对匹配点对，是ASIFT匹配结果的两倍．可见，本文改进后的ASIFT算法的确能够显著提高原ASIFT算法的特征提取数量，验证了改进算法的有效性．

利用PSO－ASIFT算法的上述匹配结果，使用Multi-GS多结构估计算法进行单应性矩阵结构提取实验．首先将PSO－ASIFT算法的匹配结果转换为Multi-GS算法的输入图像形式，如图5所示，再分别用不同颜色的符号标识出属于不同结构的点对 (红蓝绿三种颜色标识了三种结构)，而无效的点对用黄色的+号标识出．本文分别使用随机采样RANSAC算法和Multi-GS算法对上述输入数据进行多结构提取．图6和图7分别给出两种算法的多结构提取结果，对比图5—图7可知，10s的CPU时间内，RANSAC算法只得到两种有效的结构，第三种结构 (图5中绿色标识)无法得到，而Multi-GS算法命中全部三种结构 (无效点已经被删除，无标出)，且三种结构的分类比较准确．

得到上述Multi-GS多结构提取结果后，原始特征匹配结果 (图4b)中把所有无效的匹配点对去除，剩余的即为有效匹配点对．去除错误匹配点对后的结果如图8所示，共去除89对错误点对，最终匹配点对382对．

图3 输入图像Fig.3 Input images

图4 ASIFT和PSO-ASIFT算法的匹配结果Fig.4 The matches of the ASIFT and PSO-ASIFT methods

图5 多结构估计中的输入匹配点对（无效点用黄色的+标出）Fig.5 Input points of the Multi-structure estimating（the useless points maked by yellow+）

图6 随机采样算法RANSAC的多结构提取结果Fig.6 The results of random sampling RANSAC

图7 Multi-GS算法的多结构提取结果Fig.7 The results of Multi-GS

图8 去除错配点对后的最终匹配效果Fig.8 The ending matches after removing the wrong points

从实验结果可知，本文提出的PSO－ASIFT算法能比原算法提取到更大量的特征匹配点对，在此基础上利用Multi-GS多结构估计算法进行了多结构提取，进而去除了错误的匹配点对，最终得到了大量且精确的特征匹配点对．可见，本文算法是一种有效的特征提取算法．

4 结束语

本文先用变异粒子群算法对ASIFT特征提取算法进行优化，在得到大量特征匹配点的基础上又通过Multi-GS多结构估计算法对特征匹配结果进行多结构提取并且去除错误的匹配点，最终得到大量且精确的特征匹配对．通过实验结果说明本文算法是一种有效的特征提取算法，但同时发现该算法在时间效率方面还有不足，因此，如何在本文基础上尽可能提高时间效率，将是今后要继续研究的方向及重要内容．

[1]SCHAFFALITZKY F，ZISSERMAN A．Multi-view matching for unordered image sets[C]//Proceedings of the 7th European Conference on Computer Vision．Copenhagen，Denmark:Springer-Verlag，2002:414-431．

[2]FERRARI V，TUYTELAARS T，VAN GOOL L．Simultaneous object recognition and segmentation by image exploration[C]//Proceeding of the 8th European Conference on Computer Vision．Prague，Tcheque Republic:Springer-Verlag，2004:40-54．

[3]LAZEBNIK S，SCHMID C，PONCE J．Sparse texture representation using affine-invariant neighborhoods [C]//Proceedings of the Conference on Computer Vision and Pattern Recognition．Madison，Wisconsin，USA:IEEE，2003:319-324．

[4]MIKOLAJCZY K，SCHMID C．Indexing based on scale invariant interest points[C]//Proceeding of the 8th International Conference on Computer Vision．Vancouver，Canada:IEEE，2001:525-531．

[5]SE S，LOWE D，LITTLE J．Global localization using distinctive visual features[C]//International Conference on Intelligent Robots and Systems，IROS 2002．Lausanne，Switzerland:IEEE，2002:226-231．

[6]SIVIC J，ZISSERMAN A．Video google:a text retrieval approach to object matching in videos[C]//Proceedings of the 9th International Conference on Computer Vision．Nice，France:IEEE，2003:1470-1478．

[7]BROWN M，LOWE D．Recognising panoramas[C]//Proceedings of the 9th International Conference on Computer Vision．Nice，France:IEEE，2003:1218-1227．

[8]HARRIS C，STEPHENS M．A combined corner and edge detector[C]//Alvey Vision Conference．Manchester，UK:[s.n.]，1988:15-50．

[9]MIKOLAJCZYK K，SCHMID C．Scale and affine invariant interest point detectors[J]．International Journal of Computer Vision，2004，60(1):63-86．

[10]MATAS J，CHUM O，URBAN M，et al．Robust wide-baseline stereo from maximally stable extremal regions [J]．Image and Vision Computing，2004，22(10):761-767．

[11]MIKOLAJCZYK K，SCHMID C．A performance evaluation of local descriptors [J]．IEEE Trans PAMI，2005，27(10):1615-1630．

[12]MOREL J M，YU G．ASIFT:a new framework for fully affine invariant image comparison[J]．SIAM Journal on Imaging Sciences，2009，2(2):438-469．

[13]AKYILMAZ．Total least squares solution of coordinate transfor-mation [J]．Survey Review，2007，39(303):68-80．

[14]LINGWORTH J，KITTLER J．A Survey of the Hough Transform [J]．CVGIP，1988，44:87-116．

[15]MILLER V S．Use of elliptic curves in cryptography [C]//Advances in Crptology CRYPTO85．Berlin:Springer，Lecture Notes in Computer Sci，1986，218:417-428．

[16]CHUM O，MATAS J．Matching with PROSAC-progressive sample consensus[C]//CVPR．San Diego，CA，USA:IEEE，2005:1-7．

[18]WONG H S，TAT J CHIN，YU J，et al．Efficient multi-structure robust fitting with incremental top-k lists comparison[C]//Asian Conference on Computer Vision(ACCV)．Queenstown，New Zealand:Springer，Lecture Notes in Computer Sci，2010:553-564．

[20]CHIN T J，YU J，SUTER D．Accelerated hypothesis generation for multi-structure robust fitting [C]//European Conference on Computer Vision．Berlin:Spinger Berlin Heidelberg，2010:533-546．

[21]KENNEDY，EBERHART R C．Particle swarm optimization [C]//Proceeding of IEEE International Conference on Neural Networks．Piscataway:IEEE，1995:1942-1948．

[22]YOU B Y，CHEN G L，GUO W Z．Topology control in wireless sensor networks based on discrete particle swarm optimization [C]//Proceeding of IEEE International Conference on Intelligent Computing and Intelligent Systems．Piscataway，NJ，USA:IEEE，2009:269-273．