基于FCM和条件熵的风机属性约简*

玄兆燕，封红梅

(河北联合大学 机械工程学院，河北 唐山 063000)

1 引言

矿井风机是矿下作业的重要机械之一，对正常生产有很重要的作用，但其振动问题一直给人们造成很大困扰。同一种征兆往往与多种故障相对应，故障通常是多种原因并发形成的复合故障［1］，由于故障环境大都是不确定的，各种故障征兆值具有模糊性，因此在进行故障诊断时必须将检测数据转化为模糊数据，即模糊化。长期以来对于风机的振动故障诊断方法常采用基于振动频谱特征来实现，但振动的频谱特征只是反映了风机故障的部分信息，这就需要引入其它征兆进行判别，因此，如何既能充分利用振动的频谱特征这一重要故障征兆作为故障诊断的重要证据，又能综合利用反映故障不同方面信息的不同类型的故障征兆，从而可以更准确的进行故障识别，成为本文所要解决的问题，以此获得一个更简洁的诊断规则表，为专家诊断系统提供更有效的诊断规则库。

2 模糊C均值聚类分析

模糊C均值聚类(FCM)，是用隶属度确定每个数据点属于某个聚类的程度的一种聚类算法［2］。1973年，Bezdek提出了该算法，作为早期硬C均值聚类(HCM)方法的一种改进。

若对论域(研究的范围)U中的任一元素x，都有一个数A(u)∈0，1与之对应，则称A为U上的模糊集，A(u)称为u对A的隶属度。

μA(u)的大小反映了元素u对于模糊集A的隶属程度，μA(u)的值越接近1，表示u隶属于A的程度越高;μA(u)的值越接近0，表示u隶属于A的程度越低。

FCM把n个向量xi(i=1，2，…，n)分为c个模糊组，并求每组的聚类中心，使得非相似性指标的价值函数达到最小。FCM使得每个给定数据点用值在0，1间的隶属度来确定其属于各个组的程度。不过，加上归一化规定，一个数据集的隶属度的和总等于1:

3 故障征兆属性约简的理论基础

3.1 粗糙集

1982年，波兰数学家Z.Pawlak首次提出了一种处理不确定性现象的数学理论——粗糙集理论。粗糙集理论与其他处理不确定和不精确问题理论显著的区别是它无需提供问题所需处理的数据集合之外的任何先验信息所以对问题的不确定性的描述或处理可以说是比较客观的，由于这个理论未能包含处理不精确或不确定原始数据的机制，所以这个理论与概率论和模糊数学等其他处理不确定或不精确问题的理论有很强的互补性［3］。

设有一所需研究的对象组成的非空有限集合即论域U。给定一个论域U和U上的一簇等价关系S，称二元组K=(U，S)是关于论域U的知识库或近似空间。在该等价关系S当中，若P∈S，且P≠Ø，则U∩P仍然是论域U上的一个等价关系，称为P上的不可分辨关系，记做IND(P)。其中，U/IND(P)为知识库K中关于U的基本知识。

若S=(U，R)为一知识表达系统，若R可划分为条件属性集C和决策属性集D，即C∪D=R，C∩D=Ø，则称为CD决策表，其中IND(C)的等价类称为条件类，IND(D)的等价类称为决策类。

3.2 信息熵

首先引入熵的概念:设知识(属性集合)P是论域上的等价关系簇，根据不可分辨关系Xi∈U/IND(P)可以得到k类对象的组成，即{X1，X2，…Xk}，根据概率公式可得到k类对象的概率则P的熵定义为:

其中:log取以n为底的对数，H(P)表示了信息源P的信息量。

在熵的概念上引入属性熵的定义。在概率论当中联合概率密度为，根据联合概率密度公式，则此处知识(属性集合)Q相对于知识(属性集合)P的条件熵H(Q|P)定义为［4］:

其中:U/IND(P)={X1，X2，…，Xn}

U/IND(P)={Y1，Y2，…，Ym}

条件熵H(Q|P)是对所有P分类下不确定的等价类进行再划分的熵，它体现了用P对论域划分所形成的结果的不确定性。

3.3 属性约简的步骤

步骤1:根据粗糙集的不可分辨关系将知识库进行k类划分。

步骤2:去除划分结果当中的等价属性，所谓等价属性是指划分结果相同的属性。

步骤3:根据条件熵方法求得属性的重要度，在数据庞大的情况下还需找出核心属性，以便去除冗余属性。

步骤4:根据核心属性的重要度最大值对知识库决策表进行化简。

步骤5:以此类推，继续根据次最大值进行化简，直到得出最终结论。

步骤6:根据最小约简表再进一步消除该表当中的冗余属性得到最小规则表。

4 矿井风机故障征兆的属性约简

4.1 基于FCM的风机故障特征频率的分类

在故障诊断过程中，使用聚类分析法可以根据相似故障之间的某些共同之处对故障类型进行分类。常见的矿井风机故障常是基于故障发生的位置和零件的不同位置来进行分类的，本文根据故障征兆当中的特征频率对故障进行分类，然后根据其它的故障征兆进行进一步分析，从而降低故障源的数量。对故障基于特征频率进行模糊C均值聚类分析的划分故障树如图1所示。

图1 风机故障分类

4.2 基于最大隶属原则的风机故障特征的提取

最大隶属原则:设给定的论域U为全体被识别对象构成的论域，A1，A2，…An是U的n个模糊子集，u∈U是一个识别对象，若μAt(u)=max{μA1(u)，μA2(u)，…μAn(u)}，则认为u优先隶属于At，即u优先属于模式At所代表的那一类［5］。对于振动故障频谱特征采用最大隶属原则进行提取，这是因为频谱特征参数之间存在着很强的相关性，使用该方法可以剔除变量之间的相关性以及冗余性，降低数据源的分析个数，然后再对缩小的数据进行决策表分析，这样不但可以剔除干扰信息影响，而且可以降低聚类分析时输入变量的维数，简少决策表分析的计算量，根据图1当中故障树的分类以及各个故障特征频率的定位，将通频段分为了七个部分，表1为某次实现的基频故障现象表。

根据表1可得，风机的某工作状态下各个段的频率的幅值的隶属度，其中:基频的隶属度为:

表1 故障特征频率幅值

128/(128+32)=0.8

2倍频的隶属度为:

32/(128+32)=0.2

其它幅值的隶属度都为0，由最大隶属原则可知，该风机的故障类型应属于基频故障。特征频率为基频的矿井风机故障可能有转子不平衡(3类)、转子弯曲(2类)以及支撑系松动这三种情况，根据这三种 情况可得到如图2所示的基频故障树［6］。

图2 基频故障

4.3 基于粗糙集信息熵的风机故障征兆属性约简

在该系统当中，主要采用的风机故障征兆有特征频率、常伴频率、时域波形、振动稳定性、振动方向、相位特征和轴心轨迹七个参数，由故障常规分析子系统中的频谱分析可知，特征频率和常伴频率总是同时知道的，也就是说当进行频谱分析时，知道了特征频率，那么常伴频率也随之知道了，因此在此同时去掉常伴频率。各特征频率为基频的故障和故障征兆之间的关系如表2所示，其中前五列为条件属性，最后一列为决策属性。

将表2的内容进行数据的模糊离散化有助于对数据进行详细的分析，表3为离散化后的数据表。

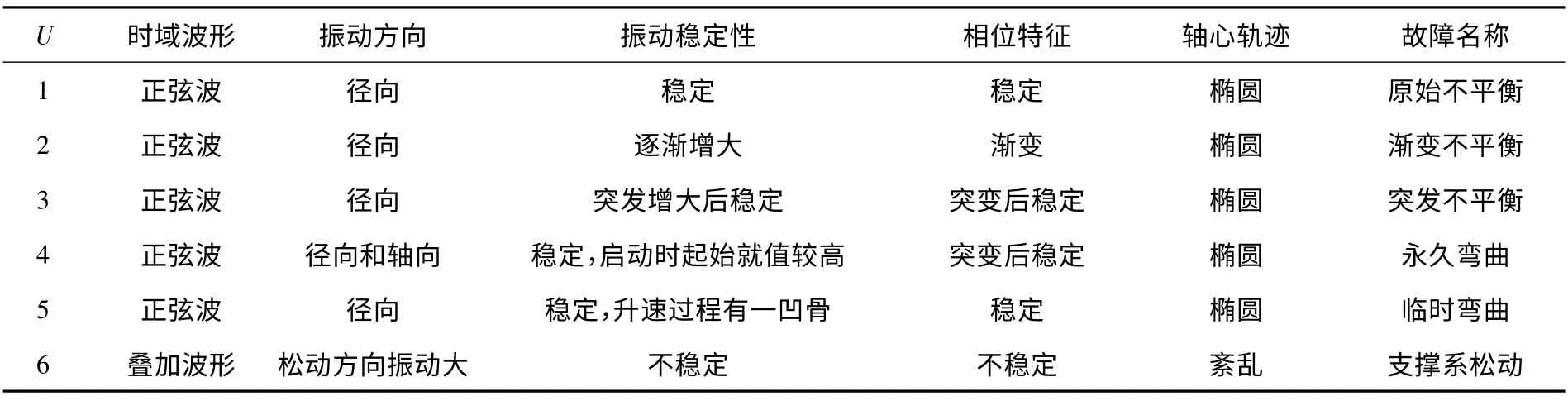
表2 故障征兆表

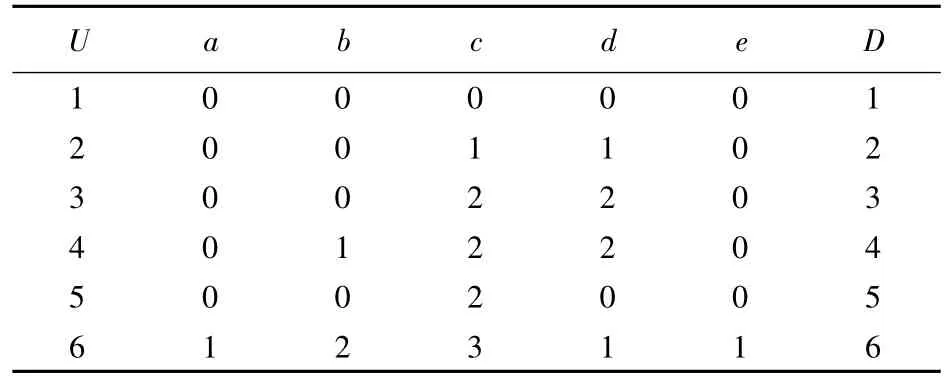
表3 离散数据表

将表3进行条件熵计算，首先根据不可分辨关系，按照条件属性和决策属性对6类对象进行分类:

在上述计算当中可以看到U/IND(a)=U/IND(e)，也就是说a属性和e属性为重复等价属性，在此略去e属性即可，接着根据式(3)计算属性熵:

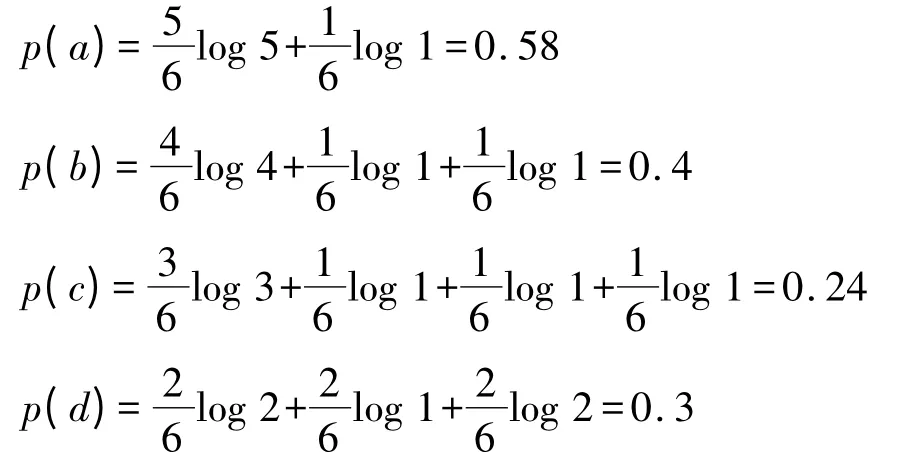
由以上数据可知属性重要度a＞b＞d＞c，再根据粗糙集的属性约简规则对故障征兆表进行约简，最终约简规则效果见表4所示。

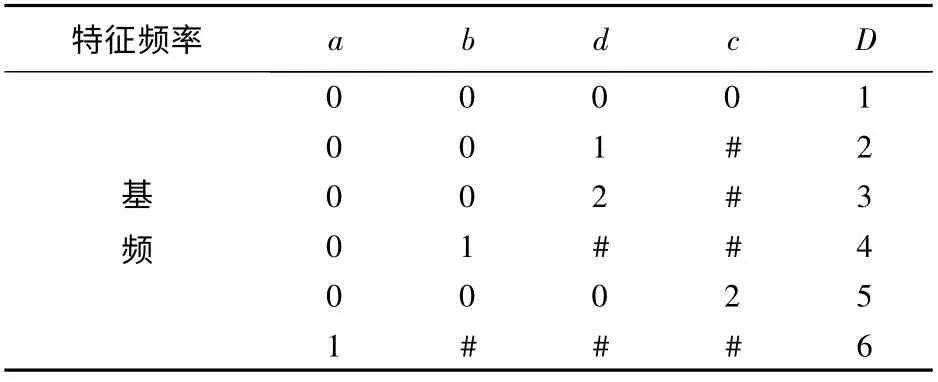
表4 最小规则表

根据表4可将所得的规则集描述为(部分):if时域波形为叠加波形then支撑系松动故障;if时域波形为正弦波and振动方向为径向and相位特征突变后稳定then突发不平衡故障。

本文以基频特征的故障现象为例，最终获得了如表4所示的最小规则表，从表4中可以看到约简了的故障征兆表可以为专家系统提供更加有效的诊断规则库。

5 总结

聚类分析是数据挖掘和模式识别中一种重要的分析方法，属性约简作为粗糙集理论的核心部分 是数据处理过程中的一个关键环节。本文提出了一种基于聚类分析法和条件熵分析法相结合的方式对多故障征兆进行分类并进行属性的约简，利用FCM算法构建故障树来缩减搜索范围，利用条件熵的属性约简形成故障诊断的规则库并实现推理。该方法既充分利用了振动的频谱特征这一重要故障征兆作为故障诊断的初步判断依据，又综合利用了反映故障不同方面信息的不同类型的故障征兆，从而做到更好的实现对大量数据的分类约简，缩小故障源的种类，进而能够更加准确地进行故障识别。

［1］ 胡友林.基于粗糙集的风机故障诊断专家系统研究［D］.武汉:武汉科技大学，2006.

［2］ 徐 天，邓廷权.基于FCM的相似关系粗糙集属性约简方法［J］.计算机工程与应用，2012(32):132-135

［3］ 李 菊.基于属性重要性的启发式属性约简算法［J］.煤炭技术，2012，31(3):201-203.

［4］ 冯晶晶，等.一种基于条件熵的决策表属性约简算法［J］.计算机应用与软件，2011(9):109-113.

［5］ 孙 芳.基于模式识别的机械设备故障智能诊断方法研究［D］.保定:华北电力大学，2007.

［6］ 郭富源.故障树理论在远程诊断系统中的应用研究［D］.大连:大连理工大学，2007.