云环境下基于MKd-Tree的大规模图数据索引技术❋
雷婷❋❋
(成都工业学院通信工程系,成都611730)
云环境下基于MKd-Tree的大规模图数据索引技术❋
雷婷❋❋
(成都工业学院通信工程系,成都611730)
由于高维属性和海量数据所带来的影响,数据管理需要相当高的计算负载,传统的集中索引技术已经变得不切实际。为满足数据的快速增长、海量和高维特性的要求,实现了一个高层次的分布式树形索引结构框架MRC-Tree。基于MRC-Tree框架基础上,提出了两种MKd-Tree索引结构构建方法,即OMKd-Tree和MMKd-Tree。理论分析和实验结果表明,基于MRC-Tree框架的MKd-Tree索引结构构建方法具有良好的可扩展性和较高的检索效率。
高维数据库;图数据;索引结构;分布式树形索引结构框架;Map-Reduce框架;MKd-Tree
1 引言
近年来,随着多媒体技术和数字化技术的进步,高维数据库的应用得到了快速的发展,如海量的多媒体数据库、生物信息学中庞大的蛋白质数据库、DNA数据库等,这些信息一般使用特征抽取等方法映射为高维数据,然后通过计算这些高维数据之间距离范数实现相似性检索。在这种背景下,高维数据索引结构和适用于高维索引结构的相似性检索算法已经成为研究人员研究的热点,而在已有的众多高维索引结构中,有的特定工作在向量空间中,而有的是针对度量空间而设计。由于度量空间概念坚实的数学基础,简单但精确的分区和减枝规则能够被成功构造。这对于建立新的索引结构是非常重要的,特别是对于检索执行耗费不仅是I/O约束的,而且是CPU约束的情况。目前,许多度量检索结构已经被提出,与线性扫描相比,性能获得显著的加速。然而,这些检索结构的执行耗费随着数据集的规模呈线性增长趋势。这意味着,随着数据规模的增大,检索反应时间迟早会变得不可容忍。另一方面,据评估,每年有近93%的多媒体数据是以数字的形式存在,新增多媒体数据的总量已经超过1 018字节,而且每年还以指数倍增长。为了能够处理海量的、不断增长的多媒体数据相似性检索,可扩展架构的需求已经促使研究人员开始重视这方面的问题。在这个研究领域,Map-Reduce框架由于良好的可扩展性和自组织性,丰富的平台支持,正在迅速获得广泛的应用,并为解决海量多媒体数据相似性检索问题奠定了坚实的基础。
尽管Map-Reduce框架[1]非常成功,但是它仅仅能够抽象独立处理单个的数据实体。大多数情况下,数据和计算密集型的应用并不适合直接使用这种简单模型。Map-Reduce框架范围之外,一类与树形结构相关的应用普遍被用在几乎所有的计算领域。基于树形结构的应用,特别是涉及大规模数据密集型处理的情况,需要使用分布式计算和存储系统。例如,使用标记语言表示的结构化文档,如SGML和它的变种XML,都是基于树形结构表示的。这些文档往往需要复杂的检索处理,并且可以有效地利用它们的树形结构实现。许多检索程序都是基于检索树的,如BST[2]、B-Trees[3]、R-Trees[4]和Kd-Tree[5],其目的都是为了使数据检索更加快捷高效。空间树形结构也已经被广泛应用于几何造型、图形和图像等高维数据处理中。在高性能计算中,基于树形结构的数据密集型应用也广泛存在,既有获取和挖掘科学数据集的应用,也有分子动力学和计算电磁学等领域的应用。
基于树形结构的数据和计算密集型应用往往需要用户大量的编程工作,特别是对于处理分布式环境中大的树形结构。基于Map-Reduce框架的抽象树形结构是非常有帮助的,但由于树形结构及其相应算法的多样性,构建一个基于Map-Reduce框架的树形结构是非常有挑战性的。参照文献[6-9],基于Hadoop环境,本文为树形结构的检索和计算实现一个高层次的分布式架构,即MRC-Tree(Computation based on Map-Reduce on tree structures),也称为树形结构上基于Map-Reduce的计算。尽管树形结构及其应用在上面的算法类型多种多样,该抽象方法可以为更广泛的应用提供充分的一般性。MRC-Tree框架包含需要用户指定的函数(由基本函数Map和 Reduce组成),通过精巧设计这些函数,可以通过多种方式实现树形结构中广泛使用的操作。这些函数都是基于基本的父子(Parent-Child)关系,因此对于所有树形结构都一样,同时,将存储机制、容错问题和并发问题等问题都移交给Hadoop平台管理。然后,在MRC-Tree框架基础上,基于原始的Kd-Tree索引结构[5],提出两种并行化Kd-Tree的方法,即MMKd-Tree(Build multiple Kd-Trees by splitting data equally based on Map-Reduce)和OMKd-Tree(Build one distributed Kd-Tree based on Map-Reduce)。Kd-Tree是一种根据K维空间中的点集对空间进行分割的数据结构,采用多维索引值进行查找,常用于范围查找和最近邻查找等,是一种特殊的二叉空间分割树。在高维空间检索,特别是图形检索,诸如碰撞检测、遮挡剔除、游戏以及光线追踪等领域[10-11]应用广泛。最后,通过实验,分别从检索CPU时间、检索精度、吞吐量以及可扩展性4个方面来评估MMKd-Tree和OMKd-Tree索引结构性能。理论分析和实验结果表明,基于MRC-Tree框架的OMKd-Tree索引结构具有良好的可扩展性和较高的检索效率。
2 MRC-Tree框架
对于树形结构,用户可以通过父节点与子节点之间链接导航的拓扑结构来访问树节点上特定的应用信息。树形结构的表示形式和存储结构对于用户是无关紧要的,即便它是以一种分布式的方式存储。本节的研究内容是在超大的树形结构上支持数据和计算密集型应用,通过实现MRC-Tree框架来提供多个并发计算,为了使算法更高效地执行,MRC-Tree框架提供分布式计算方法。MRC-Tree框架如图1所示。
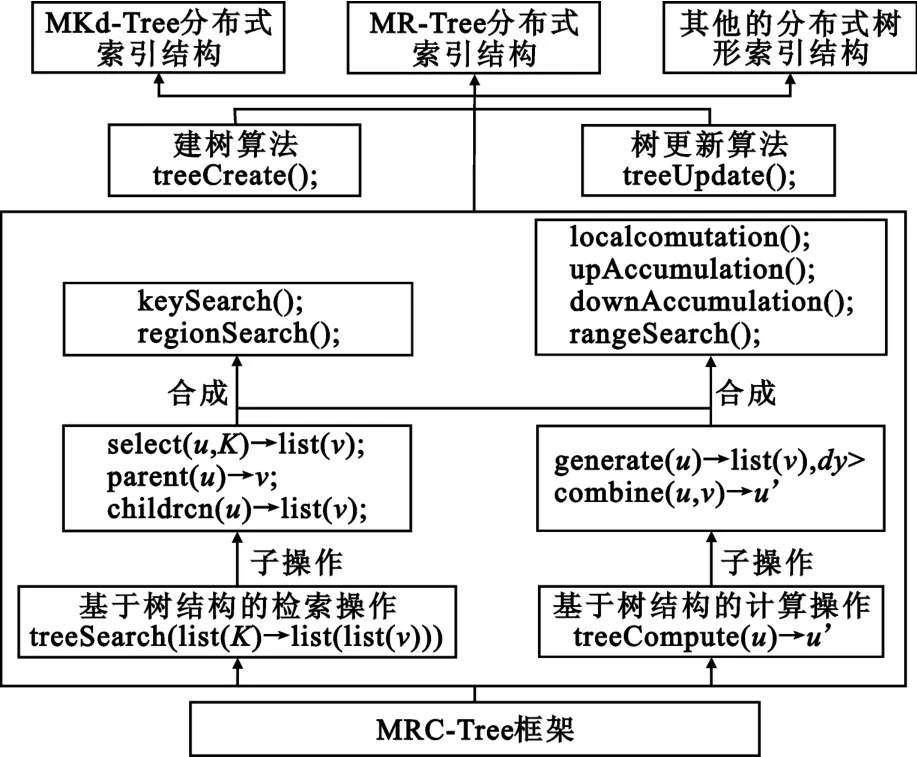
图1MRC-Tree框架结构图Fig.1 The MRC-Tree frame structure
在树形结构中,每个节点存储的信息由树的拓扑结构信息和特定的应用信息两部分组成。其中,树的拓扑信息包括父节点与子节点之间的链接、节点在树中的层次等。树形结构的节点可以表示成μ、ν、ω,在节点μ中,使用元组μ=(kμ,Xμ)表示特定的应用信息,kμ为唯一的节点标识符,Xμ为存储在节点μ中的其他信息。例如,kμ可以是二叉检索树中的编号信息、八叉树中的域信息等。kμ和Xμ的数据类型是用户指定的。使用符号“ㄧ→”表示MRC-Tree框架提供给用户的函数,符号“→”表示由用户提供的函数。MRC-Tree框架包括两个关键操作,一个操作是用来表示多个检索在树形结构上并发执行,另一个操作是用来表示在树形结构的每个节点上执行计算。这两个操作都依赖于有限的用户指定函数,通过这些精心设计的函数可以实现不同类型的树及其基于树的操作。
2.1 基于树形结构的检索操作
基于树形结构的检索操作提供了自上而下的检索,从树的根开始遍历,递归向下一个或多个分支路径遍历,从一个节点遍历至另一个或更多的子节点,检索操作的结果是一个树节点列表。尽管并行执行特定类型树形结构的单次检索一直是一个理论研究问题,为提高单次检索效率,往往选择将数据分区索引,然后通过分布式检索算法进行检索以及结果整合。实践中往往使用并发多检索和数据分区检索相结合,可以充分利用分布式系统中的计算资源。而且对于并发多重检索问题,并行计算是非常有效的。通过检索项列表,treeSearch操作允许多个并发检索同时执行,最后以list(list(ν))方式返回所有检索结果。令K表示单一检索项,即

其中,list(K)=(K1,K2,…Kn)是一个包含n个检索项的列表,而相应的结果节点列表为

操作依赖于用户指定的select函数,该函数从树形结构中取出一个节点μ,检索项K作为输入,输出一个节点列表:select(μ,K)→list(ν)。
其中,list(ν)有以下3种情况:
(1)list(ν)=(μ),这种情况下,检索停止在μ,μ被包括在检索结果集合中;
(2)list(ν)为空,检索停止,在这个检索路径上,没有节点被包含在检索结果集合中;
(3)list(ν)包含一个或多个μ的孩子,select被递归应用到list(ν)中的每个节点上。
为实现select函数,用户需要访问一个节点的孩子节点。一个节点的父节点和孩子节点分别通过以下系统指定方式获得:parent(μ)ㄧ→ν和children(μ)ㄧ→list(ν)。
2.2 基于树形结构的计算操作
函数treeCompute用于处理树形结构中的节点,计算节点中的信息:treeCompute(μ)ㄧ→μ′。其中,μ′=(kμ,X′μ)表示更新节点μ。在更新节点μ过程中,其他节点的集合也需要被考虑。用户指定如何确定与μ相关的节点列表,并通过generate函数在μ上定义交集。使用用户指定的combine函数,合并节点μ与交集中的值,计算节点μ′。generate和combine函数定义如下。
(1)generate函数:generate函数将节点μ作为输入,返回一个包含节点μ上的交集和一个依赖标识dy。这个标识用来表明,若多个交集之间存在依赖,是否需要在函数中考虑,generate(μ)→(list(ν),dy)。
(2)combine函数:合并函数需要指定如何合并关于节点μ的信息来计算它的更新值,这些信息来自节点μ的交集中所有节点,combine(μ,ν)→μ′。
2.3 映射树形结构操作到MRC-Tree框架
树形结构上的键值检索:对于一个可以完全有序集合,检索树被广泛用于索引集合中的键值检索。在MRC-Tree框架上,使用treeSearch操作在检索树上实现多个检索并发执行。操作定义如下。
(1)域检索:基于Rd(d∈N)层次划分的空间树形结构种类较多,例如:四叉树、八叉树、Kd-trees、R+-Trees等。在这种情况下,检索键值K是d维空间中的一个区域,检索结果是一个叶子节点列表,其中每个节点都对应一个与K相交的区域。
(2)局部计算:树形结构中最简单的计算操作是在树的每个节点上进行局部计算,这时,无需考虑与其他节点的交集。treeCompute可以被用来简化定义generate函数,仅需要返回节点本身,同时也可以简化combine函数的计算:

(3)向上聚类:是指对树中每个节点的数据聚类从它的后裔节点开始,并不直接从内部节点子树的所有叶子节点开始计算聚类,这样代价较大,而采用从节点孩子的聚类值进行计算。要做到这一点,在计算父节点的聚类之前,首先需要计算孩子节点的聚类值。为实现这种操作,将一个节点的交集定义为它的孩子,同时在函数generate中,将dy标识设为true。函数combine定义每个孩子节点的聚类操作,由⊕表示:
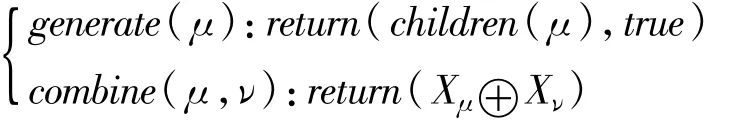
(4)向下聚类:与向上树形结构聚类相反,向下树形结构聚类是指对树中每个节点的数据聚类从它的祖先节点开始。要做到这一点,首先取得一个节点父节点的聚类值,然后同当前节点值合并。为实现这种操作,generate函数被要求返回父节点,以及将dy标识设为true,数据聚类操作⊕,被定义在combine函数中:
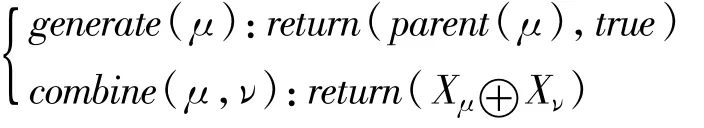
(5)范围检索:对于一个空间树形结构,树中每个节点都对应着Rd空间中的一个盒子。假设需要在树的每个节点上执行计算,计算使用的是与中心节点的距离范围为[d1,d2]的同层所有节点。
3 MKd-Tree
本文基于MRC-Tree框架,提出两种并行化Kd-Tree的方法,即MMKd-Tree(Build multiple Kd-Trees by splitting data equally based on Map-Reduce)和OMKd-Tree(Build one distributed Kd-Tree based on Map-Reduce),如图2所示。
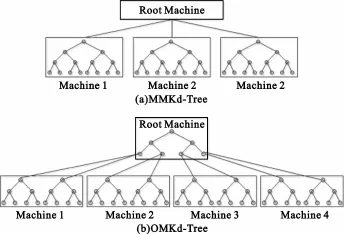
图2 基于MRC-Tree框架的Kd-Tree并行化方案Fig.2 Distributed Kd-tree schemes based on the MRC-Tree
(1)MMKd-Tree:并行化Kd-Tree最简单的方式,首先根据计算节点个数将数据集均匀切分为独立的n-1块(1个根计算节点,n-1个子计算节点),近似保证每个数据块适合子计算节点的主存。接下来,为每个数据块在子计算节点上分别建立一个独立的Kd-Tree。检索过程中,根计算节点接受目标检索特征向量,并将特征传递给所有的子计算节点,然后收集返回结果并整合,输出最终排序好的结果;
(2)OMKd-Tree:该方法并行化过程中仅仅建立一棵Kd-Tree,其上部位于根计算节点,下部被切分到各个子计算节点,存储特征的叶子节点也位于这些子节点上。检索过程中,根据Kd-Tree遍历退出位置,根计算节点引导目标检索特征向量到相应的子计算节点。子计算节点根据相应的Kd-Tree子树计算最近邻,返回结果给根计算节点。最后,根计算节点进行结果整合排序,输出最终排序好的结果。
显而易见,OMKd-Tree最大的优点是对于单个特征向量仅需要访问少量子计算节点。因此,子计算节点可以同时并行处理多个特征向量,大部分计算都发生在子计算节点中,文献[12]已经证实该方法是合理的。随着子计算节点数量的提高,根计算节点将会成为瓶颈,本文通过引入多个根计算节点副本来解决此问题。建立适用的OMKd-Tree面临两个主要挑战:一是如何建立一个包含超高维特征向量(成千上万维)的Kd-Tree,这种情况下,在单一计算节点上建立Kd-Tree是不可行的;二是在OMKd-Tree上如何实现回溯。本文通过以下两个方案来解决这两个问题。
(1)OMKd-Tree并不是在单个计算节点上建立Kd-Tree,而是在根节点上建立一个特性分布树,即Kd-Tree的上层。这是因为数据量庞大且维度较高,不可能在单个节点上满足特征向量所有维度,可以采取简单的对特征进行抽样,并在单个计算节点上使用尽可能多的内存。通过计算Kd-Tree建树算法抽样的均值,上面的方法并不会影响最终Kd-Tree的性能。
(2)OMKd-Tree方法仅在子计算节点上执行回溯算法,根节点无需回溯。为判定需要访问哪个子计算节点,需要计算到切分点之间的距离,如果距离低于判定阈值,将该计算节点包含到下一步需要处理的过程中。
基于MRC-Tree框架实现MMKd-Tree和OMKd-Tree,如图3所示,主要分为两个阶段:
(1)分布式建树阶段:特征向量Map-Reduce将向量集合切分到各个子计算节点,接下来通过索引Map-Reduce在各个子计算节点建立不同的Kd-Tree。
(2)分布式检索阶段:通过分配Map-Reduce将目标特征向量分配到合适的子计算节点,然后通过匹配计算Map-Reduce检索相应的Kd-Tree,并进行结果收集和整理,最后输出结果。

图3 基于Map-Reduce的分布式Kd-Tree机制Fig.3 Distributed Kd-Tree scheme based on the Map-Reduce
4 实验验证及性能分析
本节将显示和讨论分布式Kd-Tree索引结构在IBM集群上获得的实验结果。在实验过程中,由于分布式环境对外提供其他计算服务,本文实验过程是与其他程序共享分布式资源,因此,在实验结果上可能会出现小幅波动。分布式环境构成:1个Master管理节点服务器,8个刀片服务器(HS21)计算节点,1套8 TB磁盘阵列(IBM DS3400)存储。
4.1 数据集
在实验中使用两个不同统计类型的测试数据集,每种数据集都包括两种不同类型图像,如图4所示。

图4 数据集描述Fig.4 The dataset description
(1)测试集
已经进行标注的图像,作为参照目的。这个集合中的每个对象包括两种类型的图像:一是基准图像,表示要被检索的真实图像,用来验证检索结果的正确与否;二是测试图像集,用来查询数据库,表示与基准图像相近,由基准图像经过变换后的图像,例如不同视角、光照条件、缩放比例等。
(2)干扰集
表示构成查询数据库的大部分图像,尽管这些图像在一定统计意义上与测试图像有联系,事实上与测试图像集无关。算法必须能够识别并过滤掉这些混乱和扭曲图像,并找到基准图像。在现实的图像集构造过程中,这个集合将包括所有与基准图像语义相近的图像,例如,与基准图像相近的语义是标注为建筑类的图像。
实验过程中,使用一个Holidays图片集测试分布式Kd-tree索引结构的性能。Holidays[9](1 491幅图片,4 456个描述器,500个检索),这个数据集主要包含假日旅游的图片。扰乱数据集使用Flickr旅游图片,通过使用Flickr站点检索引擎,检索关键字为“travel”和“Holiday travel”,获取总计达1 M张各种类型的假日旅游的图片(自然、建筑、大海和火山等)。
最后,该数据集总计1 M张图片,500个检索图片,每个图片平均有1 500个描述特征。对于所有图片,总计特征为15亿。在本文中,图片特征提取方法使用SIFT算法[13]。使用下面公式进行检索精度评估:

该公式表示,检索返回的Top-k个图片中包含基准图像在检索总次数中所占的比例。其中,rq表示基准图像在检索结果中的排名,若{rq≤k}为真,则{rq≤k}=1。
对于分布式Kd-Tree,为了权衡精度和检索时间,本文限定了每个特征的回溯范围,而且这个范围由所有Kd-Tree子树共享。例如,对于MMKd-Tree,回溯限定为B=3 k,如果一个特征有两个子计算节点,则每个使用1.5 k;若是3个子计算节点,则是1 k。对于具有M个子计算节点的OMKd-Tree,每个节点使用B/M个回溯步骤。
4.2 性能分析
实验中,通过改变分布式Kd-Tree索引系统中计算节点的个数M(2≤M≤8)、距离阈值d(0.05≤
d≤0.3)、回溯步骤数Nb(512≤Nb≤30 k)、图片规模Ns(1 k≤Ns≤10 M)、检索图片次数Nr(1≤Nr≤150)来调节、测试和分析分布式索引结构的性能。
首先,使用1 M图片数据集,测试不同的参数对与分布式Kd-Tree性能的影响:距离阈值d、回溯步骤数Nb和子计算节点个数为M。
如图5所示,随着距离阈值的增大,OMKd-Tree将会访问更多的子(叶子)计算节点,由于回溯步骤Nb是固定的,叶子节点的子树不能够访问足够深度,因此检索精度会逐渐降低。而由于回溯步骤确定,检索CPU时间没有明显变化。而对于MMKd-Tree,距离阈值变化并不会影响需要访问的子计算节点,因此预测精度不会变化,检索时间会随之略微下降,因为这是显而易见的,图中并没有画出。

图5 距离阈值的影响Fig.5 The effect of the distance threshold
如图6所示,随着回溯步骤的增大,子(叶子)计算节点的个数是固定的,访问叶子节点的深度会随之增大,检索精度也随之提高,检索CPU时间也随之提高;显然,随着回溯步骤的增大,OMKd-Tree在检索精度和检索CPU时间方面,与MMKd-Tree相比更具优势。
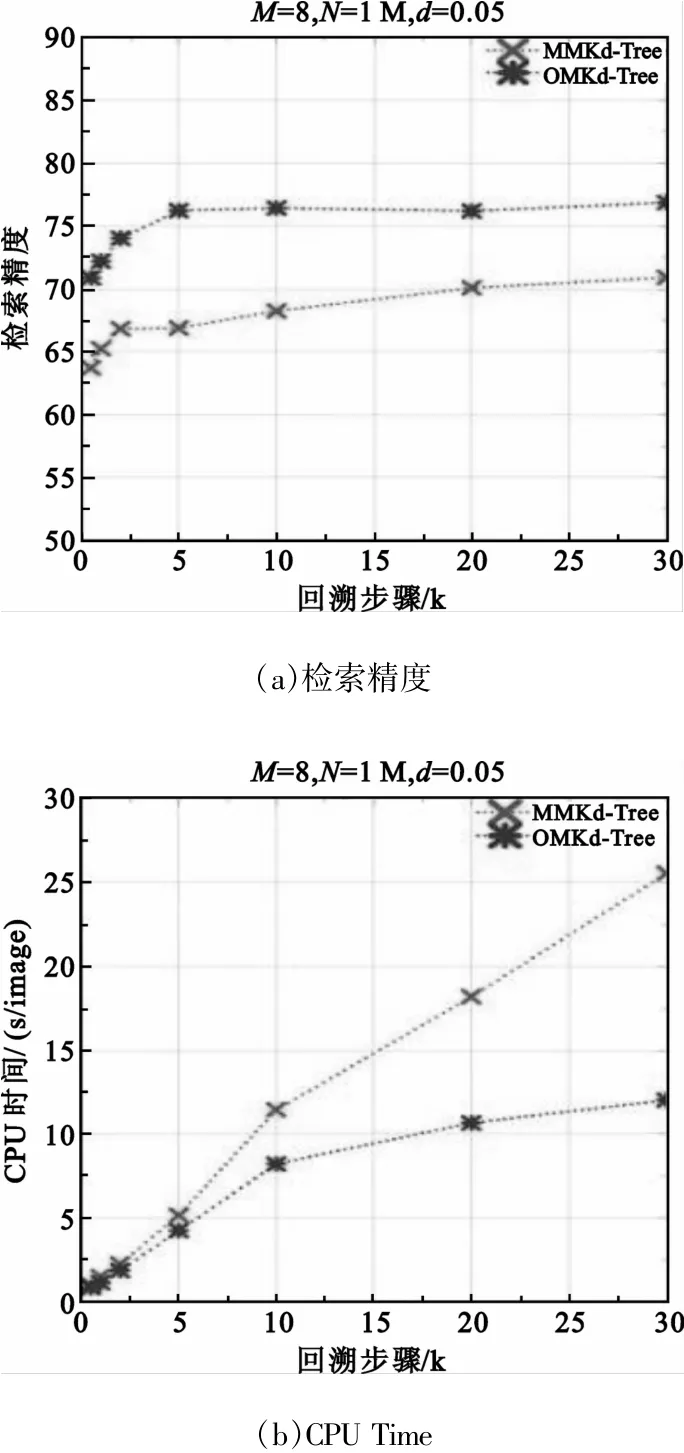
图6回溯步骤的影响Fig.6 The effect of the backtracking step
图7 显示了图像规模增长对这两种索引结构的影响。随着图像规模的增大,树的深度会随之提高,由于回溯步骤、计算节点个数和距离阈值是恒定的,所以预测精度随之下降,检索CPU时间呈上升趋势,吞吐量对于两种方法在峰值之前都成上升趋势,显然OMKd-Tree的吞吐量远高于MMKd-Tree,而且当图像规模为10 M时,OMKd-Tree吞吐量继续呈上升趋势,而MMKd-Tree开始下降。显然,与MMKd-Tree相比,OMKd-Tree具有更高的检索精度、更低的CPU时间代价和更高的吞吐量。
如图8所示,随着计算节点个数的增大,回溯步骤、数据集规模和距离阈值都恒定的情况下,OMKd-Tree的预测精度和检索CPU时间几乎不变,吞吐量明显提高;对于MMKd-Tree,预测精度下降,检索CPU时间提高,吞吐量也相应提高,但提高幅度没有OMKd-Tree明显;对于OMKd-Tree,树顶层的层数在特征Map-Reduce阶段被构造。对于MMKd-Tree,定义了图像数据集被分组的个数。对于相同数目的计算节点,OMKd-Tree的总体性能(检索精度、检索CPU时间和吞吐量)优于MMKd-Tree。特别是,随着计算节点的个数增长,OMKd-Tree的检索CPU时间几乎不变,而MMKd-Tree呈增长趋势。这是因为,尽管回溯步骤被分布到所有机器上,特征向量仍然需要拷贝并发送到所有计算节点上,内存拷贝需要耗费大量CPU时间。同时注意到,吞吐量也随着计算节点的个数增加而增加,OMKd-Tree的吞吐量远远大于MMKd-Tree。
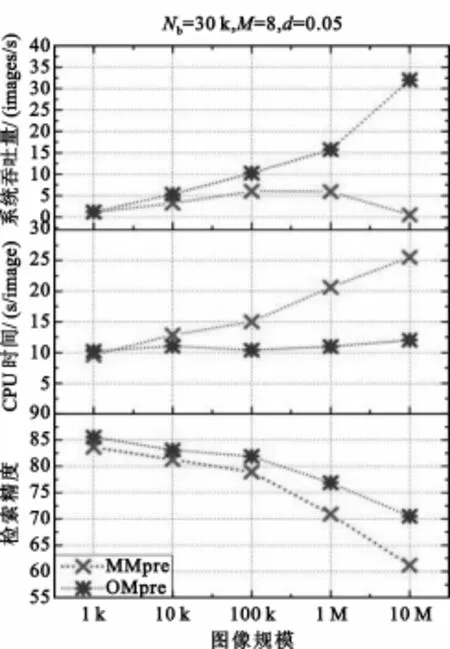
图7 图像数据库规模的影响Fig.7 The effect of image database size
图9 显示,不同Top-k的k值对于检索精度的影响,k的范围是从1~150。显而易见,随着k值增大,检索精度随之提高,而且图像规模越小检索精度越高。因为,从10 M图像库中查找一幅图像,命中正确图像的概率为10-7。显然,数据库规模越大,命中概率越低,检索精度越低。

图9Top-k查询中k值的影响Fig.9 The effect of k in the Top-k query
5 总结
本文面向云环境中大规模图像查询需求,设计了一个基于Map-Reduce模型的分布式树形结构检索和计算抽象框架MRC-Tree,实现了基于MRC-Tree的分布式的图像索引结构建立算法OMKd-Tree和MMKd-Tree,并通过实验分析了两类算法的性能。本文所提出的高维特征索引机制是一个初步尝试,尚有不少需进一步开展的工作,如对于OMKd-Tree算法,通过自适应的参数设置来进一步提高索引结构的性能;融合多种高维特征(包括高层语义特征),拓展MRC-Tree框架以适应融合特征,以达到更好的查询效果。
[1]Dean J,Ghemawat S.Map-Reduce:Simplified Data Processing on Large clusters[J].ACM Communication,2008,51(1):107-113.
[2]Heger D A.A Disquisition on the Performance Behavior of Binary Search Tree Data Structures[J].European Journal for the Informatics Professional,2004,5(5):67-75.
[3]Comer D.The Ubiquitous B-Tree[J].ACM Computing Surveys,1979,11(2):121-137.
[4]Guttman A.R-Trees:A Dynamic Index Structure for Spatial Searching[C]//Proceedings of the 1984 ACM SIGMOD International Conference on Management of data.New York:ACM,1984:47-57.
[5]Bentley J L.Multidimensional binary search trees used for as-sociative searching[J].ACM Communication,1975,18(9):509-517.
[6]Abhinav SARJE,Srinivas ALURU.A Map-Reduce Style Framework for Trees[R].Technical Report,2009.
[7]Sarje A,Aluru S.A Map-Reduce Style Framework for Computations on Trees[C]//Proceedings of 2010 39th International Conference on Parallel Processing.San Diego,California,USA:IEEE,2010:343-352.
[8]杨恒,王庆,何周灿.面向高维图像特征匹配的多次随机子向量量化哈希算法[J].计算机辅助设计与图形学学报,2010,22(3):494-510. YANG Heng,WANG Qing,HE Zhou-can.Multiple Randomized Sub-vectors Quantization Hashing for High-Dimensional Image Feature Matching[J].Journal of Computer-Aided Design&Computer Graphics,2010,22(3):494-502.(in Chinese)
[9]Silpal-Anan C,Hartley R.Optimised KD-trees for fast image descriptor matching[C]//Proceedings of 2008 IEEE Conference on Computer Vision and Pattern Recognition.Anchorage,AK:IEEE,2008:1-8.
[10]过洁,徐晓旸,潘金贵.虚拟场景的一种快速优化Kd-Tree构造方法[J].电子学报,2011,39(8):1811-1817. GUO Jie,XU Xiao-yang,PAN Jin-gui.Build Kd-Tree for Virtual Scenes in a Fast and Optimal Way[J].Acta Electronica Sinica,2011,39(8):1811-1817.(in Chinese)
[11]Aly M,Munich M,Perona P.Indexing in large scale image collections:Scaling properties and benchmark[C]//Proceedings of the 2011 IEEE Workshop on Applications of Computer Vision.Kona,HI:IEEE,2011:418-425.
[12]Jegou H,Douze M,Schmid C.Hamming embedding and weak geometric consistency for large scale image search[C]//Proceedings of 2008 10th European Conference on Computer Vision:Part I.Marseille,France:IEEE,2008:304-317.
[13]Lowe D G.Object recognition from local scale-invariant features[C]//Proceedings of the 7th IEEE International Conference on Computer Vision.Kerkyra:IEEE,1999:1150-1157.
LEI Ting was born in Chenzhou,Hunan Province,in 1981.She is now a lecturer with the M.S.degree and also a CCF member.Her research concerns data mining,clound computing.
Email:tinglei.uestc@gmail.com
Large Scale Graph Data Index Based on MKd-Tree in Cloud Environment
LEI Ting
(Department of Communication Engineering,Chengdu Technological University,Chengdu 611730,China)
Managing the high-dimensional,large-scale data needs extremely high computational load.Traditional centralized indexing techniques apparently become impractical.To address the demanding needs caused by this rapidly growing,large-scale,and high-dimensional information ecology,a high-level distributed framework for searches and computations on tree indexing structures based on Map-Reduce in the Hadoop environment,MRCTree(Computation based on Map-Reduce on tree structures)is achieved.And then,two MKd-Tree(Kd-Tree based on Map-Reduce)index structures based on MRC-Tree framework,OMKd-Tree(Build one distributed Kd-Tree based on Map-Reduce)and MMKd-tree(Build multiple Kd-Trees by splitting data equally based on Map-Reduce)are proposed.Finally,the theoretical analysis and experiment results illustrate that the methods are highly effective and extensible to the similarity search in high-dimensional data environment.
high-demensional database;graph data;index structure;distributed tree index structure framework;Map-Reduce framework;MKd-Tree
date:2013-01-05;Revised date:2013-06-18
❋❋通讯作者:tinglei.uestc@gmail.comCorresponding author:tinglei.uestc@gmail.com
TP391
A
1001-893X(2013)07-0909-08

雷婷(1981—),女,湖南郴州人,硕士,讲师,CCF会员,主要研究方向为海量数据挖掘、云计算。
10.3969/j.issn.1001-893x.2013.07.017
2013-01-05;
2013-06-18

