改进的分布式扩散符号LMS算法*

陈文晓,卢光跃,2,**,黄庆东

(1.西安邮电大学通信与信息工程学院,西安710121;2.长江大学电信学院,湖北荆州434102)

改进的分布式扩散符号LMS算法*

陈文晓1,卢光跃1,2,**,黄庆东1

(1.西安邮电大学通信与信息工程学院,西安710121;2.长江大学电信学院,湖北荆州434102)

针对无线传感器网络(WSN)中数据运算量大及传输速率受限问题,提出了在分布式扩散LMS算法中先后采用符号函数和改进的符号函数量化策略,实现对误差和估计信号的量化,以减少多节点无线传感器网络的运算量和通信量。仿真结果表明,采用符号函数的量化策略时,误差相对较大;采用改进的符号函数量化策略,在设定适当的量化门限时,所提出的算法性能十分接近非量化的扩散LMS算法,且优于非协作算法。特别对于BPSK信号,相较于传统的扩散LMS算法,性能更为优良。

无线传感器网络;分布式算法;扩散LMS;量化

1 引 言

无线传感器网络(Wireless Sensor Network, WSN)能够利用节点间的相互通信来实现对监测区域的监测或目标跟踪,其在环境监测、防火救灾、目标跟踪等众多领域都表现出了广阔的应用前景[1]。然而,在无线传感器网络中,由于单个节点的能量、感知范围和信息处理能力有限,故借助于多点协作策略能够有效实现对监测区域的信号估计或目标跟踪。

在利用WSN进行信号估计时,根据其是否依赖中心节点,估计算法可分为集中式算法和分布式算法。集中式算法要求各节点将观测数据传输到中心节点并由中心节点完成数据融合,因此中心节点负荷较重,易造成网络拥塞,容错能力差;而分布式算法不依赖于中心节点,通过节点之间的协作实现对信号的估计[2]。到目前为止,众多的分布式算法都是由不同的自适应算法结合不同的协作策略而得到的。

当WSN中的节点较少时,如果把节点规划成一个环形的循环结构,信息按顺序方式从一个节点发送到与其相邻的节点,该策略即为增量(Incremental)协作方式。据此协作方式,研究者分别提出了增量LMS算法[3]及归一化增量LMS算法[4]。为了提高LMS类算法的收敛速度,文献[5]提出了增量RLS算法。这种增量协作方式虽然能耗和通信量较小,但是它需要把所有的节点规划成一个环形结构,这限制了其在由大量节点组成的WSN中的应用。为了不受网络拓扑结构的限制,充分利用网络的联通性,文献[6]提出了基于扩散算法的协作策略方式,并结合LMS、最小二乘和Kalman滤波分别提出了扩散LMS算法[7]、扩散RLS算法[8]和扩散Kalman算法[9]。文献[10]提出与扩散协作方式相似的一致滤波协作方式,并成功应用于频谱感知中[11],这种协作方式虽然简单易行,但缺乏稳健性。上述算法根据不同的需要可以应用于不同场景中,其中扩散LMS算法以其简单的分布式结构和算法稳健性而引起广泛关注。

然而,扩散LMS算法假设各节点的能量和数据交换是无限制的,但实际WSN中各节点能量、处理能力和通信信道容量都是有限的[12]。针对这样的问题,可采用量化技术来减少算法计算量和通信量,从而也减小传感器网络中节点能量的损耗。

本文先把符号函数应用到扩散LMS算法中,得到扩散符号LMS算法。为提高算法精度,用改进符号量化策略代替符号函数,得到改进的扩散符号LMS算法,该算法能够有效减小自适应过程中的运算量。最后对算法进行了仿真验证,并与扩散LMS算法和非协作算法进行了性能比较。

2 算法分析

2.1 扩散LMS算法

假定用于测量监测区域未知向量x0∈RM×1的无线传感器网络可以用如图1所示的无向图G=(V, E)来表示,其中V={1,2,…,N}为节点集合,E= {(k,l)k,l∈V}为互通链路的集合,当且仅当节点k和节点l有通信链接时,满足(k,l)∈E。Nk={l∈V(k,l)∈E}∈V为节点k的邻居节点集合,记其邻居节点的个数(也称该节点的度)为Nk,例如节点1的邻居节点集合为N1={1,2,N},N1=3。假设节点k在第i时刻的观测值yk(i)和观测向量hk(i)都是零均值的随机过程。

图1 由N个节点组成的WSNFig.1 WSN with N nodes

测量数据的信号模型为

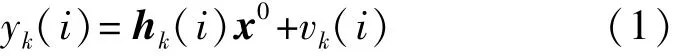
其中,vk(i)是方差为且在时间和空间上都相互独立的背景噪声。

为了从观测值yk(i)中估计出x0,扩散LMS算法[6]要求节点k连续不断地融合其邻居节点的估计值xj(i-1)(j∈Nk),得到节点k对x0的融合估计值φk(i-1)(图2(a)),并把其迅速输入到节点k局部自适应滤波器中来更新xk(i)[7](图2(b))。其对应的扩散LMS算法可表示为[7]

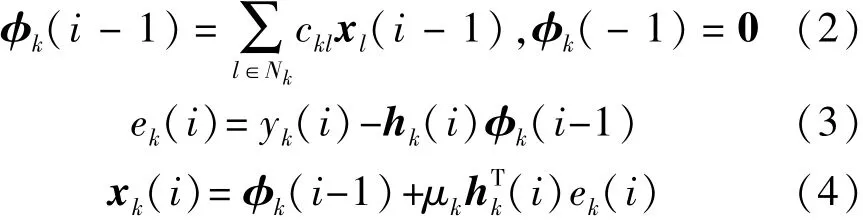
其中,常数μk＞0是收敛步长,非负的ckl(k=1,2,…, N)是局部融合参数,其满足

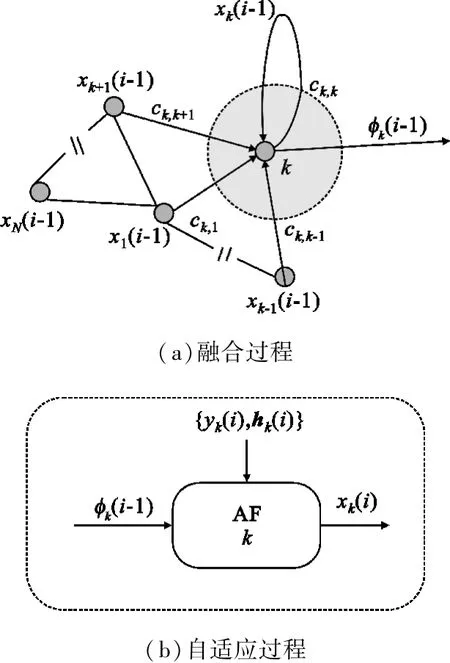
图2 扩散协作策略的网络结构Fig.2 Network with a diffusion cooperation strategy

2.2 扩散符号LMS算法

在扩散LMS算法中,当前节点需要和邻居节点进行不间断的数据传输,也就要求节点能量和信道容量为无限大[13],这在数字通信网络中是不现实的。为了减少算法的计算量或通信量,把图3所示的符号量化策略[12]应用到扩散LMS算法中,得到一类扩散符号LMS算法。

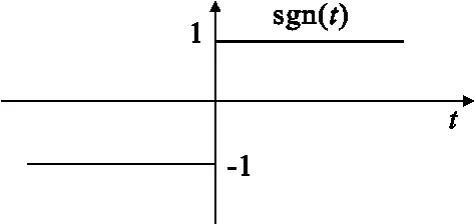
图3 符号函数Fig.3 Sign function

其中,符号函数

在这类算法中,若对式(4)中的误差信号ek(i)进行符号运算时,则得到“符号-误差”算法为

若对式(2)中的估计信号xl(i-1)进行符号运算,即

则对应的算法为“符号-数据”算法。

若对扩散LMS算法中的误差ek(i)和估计信号xl(i-1)同时进行符号运算时,则得到“符号-符号”算法。

“符号-误差”算法可看作是对误差进行两级量化。与扩散LMS算法相比较,该算法主要优点是计算量小,把一个数据量化为1 b,但其较大的量化误差将引起信号估计性能上有所退化,稳态误差增加;而“符号-数据”算法在降低算法计算量的同时,也减小了各节点间的通信量。与“符号-误差”算法不同的是,“符号-数据”算法改变了参与本节点数据融合的邻居节点估计值,结果使该算法的鲁棒性不如“符号-误差”算法。“符号-符号”算法是对误差和估计信号同时进行量化的,这样的量化使误差更大。总的来说,“符号-符号”算法的收敛速率比扩散LMS算法慢,且超量均方误差(EMSE)也将更大。

2.3 改进的扩散符号LMS算法

为了能够更进一步提高算法精度,把只有两级量化的符号量化改进为如图4所示的三级量化策略,从而得到改进的扩散符号LMS算法。

图4 改进的符号函数Fig.4 Modified sign function

其中,改进的符号函数msgn{·}的表达式为

在这类算法中,若对式(4)中的误差信号ek(i)用改进的符号函数进行运算时,则得到“改进符号-误差”算法,即

若对式(2)中的估计信号xl(i-1)用改进的符号函数进行运算,即

则得到相应的“改进符号-数据”算法。

“改进符号-误差”算法对误差ek(i)进行了三级量化运算,于是,当输入误差信号ek(i)小于设定的量化门限值δ时,ek(i)将等于零,不用对信号进行估计运算,因而能有效降低计算量。而当误差信号ek(i)大于设定的量化门限值δ时,

更新方程可写为

它相当于采用与误差信号相适应的时变步长。由此可见,该算法的收敛速度和信号追踪性能与门限值δ有关。同样,“改进符号-数据”算法对估计信号进行了三级量化,在减小计算量的同时,也大大减小了各节点间的通信量。

2.4 收敛性能分析

由于“改进符号-数据”相对误差较大,本文不深入研究,只对“改进符号-误差”算法进行详细分析。

这类算法收敛性能分析可借鉴常规LMS算法收敛性能的分析方法[14]进行。为了便于分析,设算法式(9)中融合参数矩阵C=I。对式(9)两边取统计平均,即

其矩阵的形式为

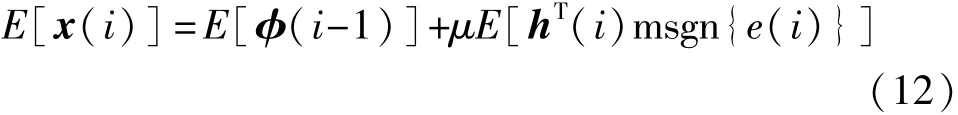
式中,第二项可借助于下面定理进行分析。

定理[12]:如果u和v是分别服从N(0,σu)和N(0,σv)的两个随机变量,并且E{uv}=ρσuσv,^v= msgn{v,δ},则

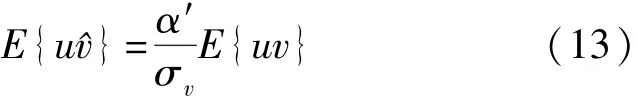
利用定理,于是

把维纳滤波器的最优解Rhy=Rhhx*代入上式,得

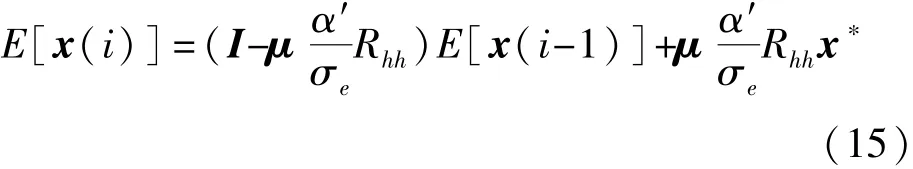
令Vi=x(i)-x*,则E[Vi]=E[x(i)]-x*。于是,将式(14)两边同时减去x*,可得到

对Rhh进行特征值分解,即Rhh=QΛQ-1,Λ是由Rhh的特征值组成的对角矩阵。令V=QV′,则

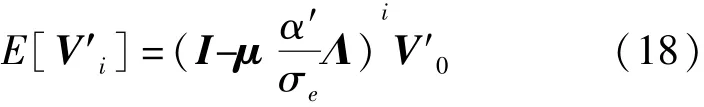
故其收敛的条件为

由于Vi=x(i)-x*为偏差向量,表示估计信号对期望信号的偏差,V=QV′,由式(18)可知其递推解是

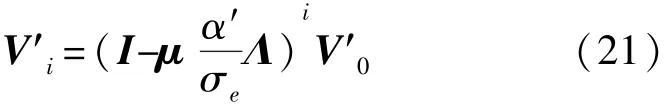
令V′=QTV=[v′1,v′2,…,v′N]T,则第j个分量的递推方程是

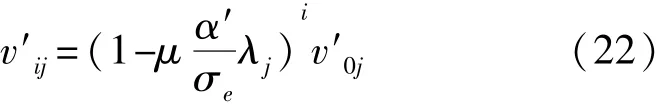
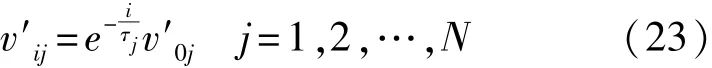
上式说明第j个分量v′j按指数规律变化,其时常数为

因为一般(α′/σe)μ都较小,可以近似为

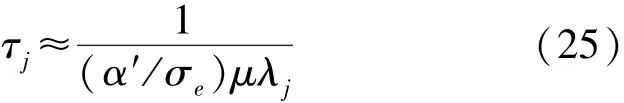
其变化规律与特征值λj和量化门限δ有关,不同的λj和δ对应的收敛时间不一样,最终的收敛取决于最慢的指数过程,它的时常数最大,对应是最小的特征值和最大的δ。

3 仿真与性能分析

采用全局均方偏差(MSD)评价算法性能,

其中,x(i)=[x1(i),…,xN(i)]和x(0)=[x0,…,x0]是各节点估计信号和初始信号的矩阵形式。在下面的仿真中,将对所提出的扩散符号LMS算法与非量化的和非协作(融合参数ckl=1,k=l且ckl=0,k≠l)算法分别进行比较。

本文的仿真采用与文献[12]相同的仿真条件。网络由20个节点组成,其拓扑结构如图5所示;未知向量设定为x0=[1 1 1 1]T,每个节点的背景噪声vk(i)的方差如图6所示。扩散算法步长设定为μk= 0.05,k=1,2,…,N,融合参数为且ckl=0,l∉Nk。仿真结果都是通过100次独立实验得到的。

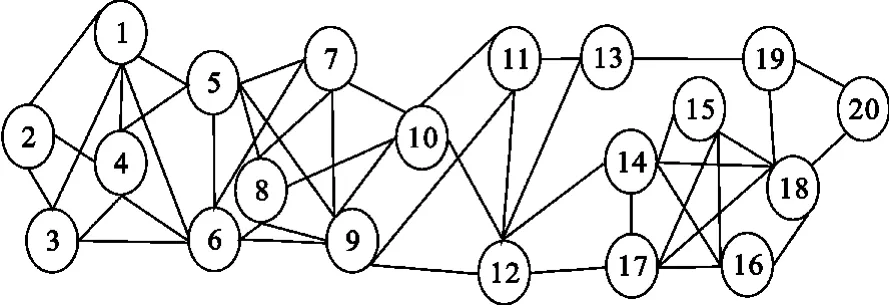
图5 网络拓扑结构Fig.5 Network topology

图6 各节点背景噪声方差Fig.6 Variances of the background noise for each nodes

图7 给出了扩散符号LMS算法与非量化、非协作算法的仿真结果。从图7可见,用两级量化的扩散符号算法能够很快收敛,“符号-符号”算法、“符号-数据”算法和“符号-误差”算法都是在迭代不到50次时就达到了平稳状态,偏差分别达到-12 dB、-15 dB和-26 dB;而非协作算法在迭代300次以后才达到稳定,偏差达到-33 dB;非量化(即扩散LMS)算法在迭代200次时达到平稳,其偏差达到-41 dB。比较可知,符号类算法收敛速度快,但是偏差较大;在3种扩散符号算法中,“符号-误差”算法的偏差最小,与前面的分析是一致的。

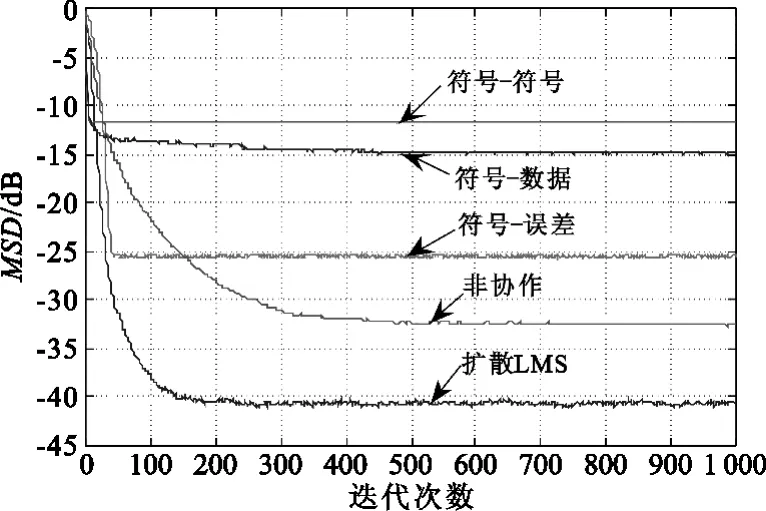
图7 扩散符号LMS算法与非量化、非协作算法比较Fig.7 Comparison among diffusion sign LMS algorithm, no-quantization algorithm and no-cooperation algorithm

图8 给出了“改进符号-误差”算法与非量化、非协作算法的仿真结果。从图8可见,当δ=0时(即为“符号-误差”算法),在迭代50次时就达到平稳状态,偏差为-26 dB;当δ=0.1时,也是在迭代50次达到平稳,偏差达到了-28 dB左右;当δ=0.2时,迭代100次左右达到平稳状态,偏差达到了非协作算法的水平-33 dB,而非协作算法在迭代近400次时才达到平稳状态;当δ=0.3时,该算法和非量化(即扩散LMS)算法收敛速度相近,都是在迭代200次左右时达到平稳状态,偏差分别为-37 dB和-41 dB;当δ=0.4时,在迭代500次时能够达到稳定状态,且其偏差达到了-39 dB,已经接近了扩散算法的偏差水平。从图8还可以看出,在δ≥0.2时“改进符号-误差”算法的性能优于非协作算法;其收敛速度会随着量化门限δ的增加而变慢,和理论分析即式(25)相一致。

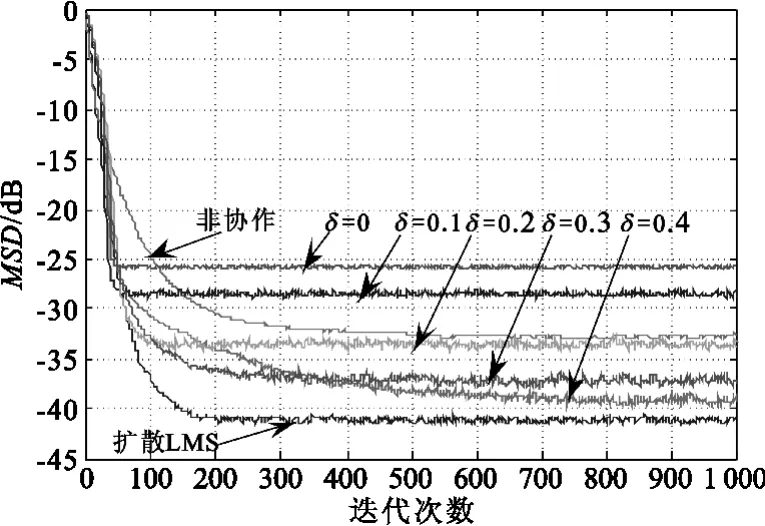
图8 不同δ时“改进符号-误差”算法的偏差Fig.8 MSD of the“modified sign-error”algorithm with different δ

图9 给出“改进符号-数据”算法与非量化、非协作算法的仿真结果。当δ=0(即为“符号-误差”算法)、δ=0.1和δ=0.2时,算法的偏差分别为-15 dB、-22 dB和-45 dB。尤其是δ=0.2时,算法比扩散LMS算法达到平稳时的偏差水平-41 dB还要小,并且都是在迭代不到50次就达到平稳状态。此时设定的已知信号值为1,若信号值为-1时也能达到同样的效果,所以信号源若为BPSK信号时,该算法将优于扩散LMS算法。

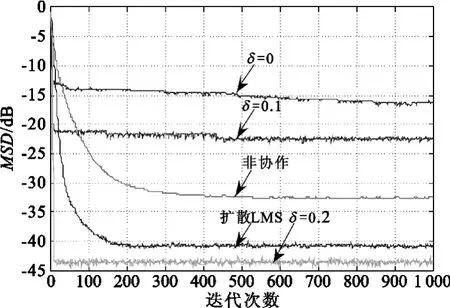
图9 不同δ时“改进符号-数据”算法的偏差Fig.9 MSD of the“modified sign-data”algorithm with different δ

从仿真的结果可见:

(1)“改进符号-误差”算法在有效减小计算量情况下,其收敛速度和跟踪性能与门限值δ有关,与其他算法相比,具有更好的可控性;

(2)“改进符号-数据”算法不但能减小算法的计算量,而且能有效减小各节点间的通信量,特别对BPSK信号时,该算法优于扩散LMS算法。

4 结束语

本文提出了一种适合于网络数据传输速率有限的分布式自适应算法,即把符号函数和改进的符号函数分别应用到扩散LMS算法中。对误差信号和估计信号分别进行量化,与非协作、非量化算法相比,有效减小了计算量和通信量。仿真结果表明,当设定适当的量化门限值时,所提出的“改进符号-误差”算法接近于扩散LMS算法性能,并且优越于非协作扩散算法。特别对于BPSK信号,“改进符号-数据”算法能在很大程度上减小各节点间的通信量,并且性能优于扩散LMS算法。对于更高级别的量化将另文研究。

[1] Estrin D,Girod L,Pottie G,et al.Instrumenting the world with wireless sensor networks[C]//Proceedings of 2001IEEEInternationalConferenceonAcoustics, Speech,and Signal Processing.Salt Lake City:IEEE, 2001:2033-2036.

[2] 白辉,卢光跃,王晓侃.非信任环境中一致卡尔曼滤波的数据融合算法[J].西安邮电学院学报,2012,17 (5):10-14.

BAI Hui,LU Guang-yue,WANG Xiao-kan.Data fusion algorithm based on consensus Kalman filter in untrustworthy environment[J].Journal of Xi'an University of Posts and Telecommunications,2012,17(5):10-14.(in Chinese)

[3] Lopes C G,Sayed A H.Incremental adaptive strategies over distributed networks[J].IEEE Transactions on Signal Processing,2007,55(8):4064-4077.

[4] Sayed A H,Lopes C G.Adaptive processing over distributed networks[J].IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences, 2007,90(8):1504-1510.

[5] Ram S S,Nedic A,Veeravalli V V.Stochastic incremental gradient descent for estimation in sensor networks [C]//Proceedings of the Forty-First Asilomar Conference on Signals,Systems and Computers.Monterey: IEEE,2007:582-586.

[6] Lopes C G,Sayed A H.Diffusion least-mean squares over adaptive networks[C]//Proceedings of 2007 IEEE International Conference on Acoustics,Speech and Signal Processing.Honolulu:IEEE,2007:917-920.

[7] Lopes C G,Sayed A H.Diffusion least-mean squares over adaptive networks:Formulation and performance analysis[J].IEEE Transactions on Signal Processing,2008, 56(7):3122-3136.

[8] Cattivelli F S,Lopes C G,Sayed A H.Diffusion recursive least-squares for distributed estimation over adaptive networks[J].IEEE Transactions on Signal Processing, 2008,56(5):1865-1877.

[9] Cattivelli F S,Lopes C G,Sayed A H.Diffusion strategies for distributed Kalman filtering:formulation and performance analysis[C]//Proceedings of 2008 1st International Workshop on Cognitive Information Processing.Santorini,Greece:IEEE,2008:36-41.

[10] Li Z,Yu F R,Huang M.A distributed consensusbased cooperative spectrum-sensing scheme in cognitive radios[J].IEEE Transactions on Vehicular Technology,2010,59(1):383-393.

[11] 王晓侃,卢光跃,包志强,等.一种新的分布式协作能量检测算法[J].电讯技术,2012,52(9):1480-1485.

WANG Xiao-kan,LU Guang-yue,BAO Zhi-qiang,et al.A Novel Distributed Cooperative Energy Detection Algorithm[J].Telecommunication Engineering,2012, 52(9):1471-1476.(in Chinese)

[12] Sadoghi Y H,Lotfizad M,Fathy M.Car tracking by quantized input LMS,QX-LMS algorithm in traffic scenes[J].IEE Proceedings-Vision,Image and Signal Processing,2006,153(1):37-45.

[13] Xie S L,Li H R.Distributed LMS with limited data rate [J].Electronics Letters,2011,47(9):541-542.

[14] 丁玉美,阔永红,高新波.数字信号处理-时域离散随机信号处理[M].西安:西安电子科技大学出版社, 2002:63-77.

DING Yu-mei,KUO Yong-hong,GAO Xin-bo.Digital Signal Processing-Discrete Time Random Signal Processing[M].Xi′an:Xidian University Press,2002:63 -77.(in Chinese)

CHEN Wen-xiao was born in Nanyang, Henan Province,in 1985.He is now a graduate student.His research concerns date fusion in wireless sensor network.

Email:164921697@qq.com

卢光跃(1971—),男,河南南阳人,1999年于电子科技大学获博士学位,现为教授,主要研究方向为现代移动通信中信号处理;

LU Guang-yue was born in Nanyang,Henan Province,in 1971.He received the Ph.D.degree from Xidian University in 1999.He is now a professor.His research concerns signal processing in modern mobile communication.

Email:tonylugy@163.com

黄庆东(1977—),男,2011年于西安电子科技大学获博士学位,现为副教授,主要研究方向为自适应信号处理及分布式算法。

An Improved Distributed Diffusion Sign-LMS Algorithm

CHEN Wen-xiao1,LU Guang-yue1,2,HUANG Qing-dong1

(1.School of Communication and Information Engineering,Xi′an University of Posts and Telecommunications, Xi′an 710121,China;2.School of Electronics&Information,Yangtze University,Jingzhou 434102,China)

To deal with the problem of heavy computation and limited data rate in Wireless Sensor Network (WSN),a quantization scheme with the sign and the modified sign functions in the diffusion least-mean square(LMS)algorithm is proposed in this paper.It can effectively reduce the computational complexity and communication burden when applied to quantify the error signal and the estimated signal in WSN. Simulation results show that the performance of the proposed scheme with appropriate quantization threshold is approaching to the non-quantitative diffusion LMS algorithm and is superior to the non-cooperative algorithm.Especially for the BPSK signal,the proposed“modified sign-data”scheme outperforms the traditional diffusion LMS algorithm.

wireless sensor network;distributed algorithm;diffusion LMS;quantization

g-dong was born in 1977.He

the Ph.D.degree from Xidian University in 2011.He is now an associate professor.His research concerns adaptive signal processing and distributed algorithm.

The National Key Technology Research and Development Program of the Ministry of Science and Technology of China (2012ZX03001025-004);The National Natural Science Foundation of China(No.61271276);The Research Program of Education Bureau of Shaanxi Province(11JK0925);The Soft Science Research Project of MIIT(2013R36-2)

TN911.7

:A

:1001-893X(2013)12-1580-06

陈文晓(1985—),男,河南南阳人,硕士研究生,主要研究方向为无线传感器网络中的数据融合;

10.3969/j.issn.1001-893x.2013.12.008

2013-08-05;

2013-11-19 Received date:2013-08-05;Revised date:2013-11-19

国家科技重大专项(2012ZX03001025-004);国家自然科学基金资助项目(61271276);陕西省教育厅自然科学研究项目(11JK0925);工信部通信软科学研究项目(2013R36-2)

**通讯作者:tonylugy@163.com Corresponding author:tonylugy@163.com

Email:huangqingdong@xupt.edu.cn