无霜冰箱翅片蒸发器通风阻力研究

李成武

1 概述

目前无霜冰箱在国内市场占有率加大，消费者对无霜冰箱的接受程度越来越高，也说明无霜冰箱的技术得到较大的进步，尤其在控制、性能与可靠性等方面取得较大的进步，对比以前的无霜冰箱主要存在能耗大、噪音大，食物容易风干等问题也得到较大的改进。作为对无霜冰箱的研究，尤其在许多的关键零部件方面的性能研究，目前还不是非常充分，例如在翅片蒸发器方面，主要是关注换热系数与换热面积，而对于通风的阻力研究还存在许多不足，这也与许多的研究工具或研究基础条件不足有关。虽然目前大量采用计算机进行CAE模拟计算，但它的结果也需要通过实际的测试进行修正，另外这种工具只是对单件进行辅助设计分析，对于快速计算与动态仿真分析还是有不方便的地方。综合上述问题的分析，本论文主要是通过对翅片蒸发器的结构特点进行分析，在基于蒸发器的生产工艺与设计变化的特点，研究影响蒸发器阻力的关键因素，确定建立分析计算的数学模型，结合许多的通风经验数据，计算出蒸发器结构的变化与通风阻力变化之间的关系式，并通过风洞试验设备的测试数据，对计算的结果进行检验与修正，从而为快速确定各种蒸发器的通风阻力计算，并为仿真分析系统提供计算方程，研究如何提高无霜冰箱的性能，以及降低噪音等。

图1 斜排翅片蒸发器的正面图

2 蒸发器计算模型设计

对于翅片蒸发器的模型建立，首先要了解蒸发器的结构特点，如图1与图2为蒸发器的整体结构。

从图1中可以见到上部的翅片间距小，距离为5mm，下部间距为10mm，这种结构设计适合无霜冰箱的结霜特点:下部结霜量大，容易堵塞蒸发器的翅片间距，加大下部的距离可以改善蒸发器的换热效果。这种翅片间距的设计对于批量生产有利，可以提高生产效率;翅片为整体翅片，铝管为整体铝管，中间无需焊接，质量的可靠性更高。但是由于铝管与翅片间的传热效果差一点，但可以通过加大铝管的表面积得到补偿。

从图2中可以看到铝管的高度间距为19mm，斜排式设计，翅片的深度尺寸为60mm。在实际的应用中，蒸发器两端因为无翅片，一般都进行密封，阻止空气流过。这样对于设计来说，主要通风是在有翅片的蒸发器中间位置，所以在图1中尺寸为L为计算通风的主要参数。

针对蒸发器的这种结构，可以将蒸发器分为5mm间距和10mm间距的空间模型，将蒸发器划分为小格后，建立计算模型如图3和图4。

对于一般翅片蒸发器的尺寸，其参数可参见表1中的数据。

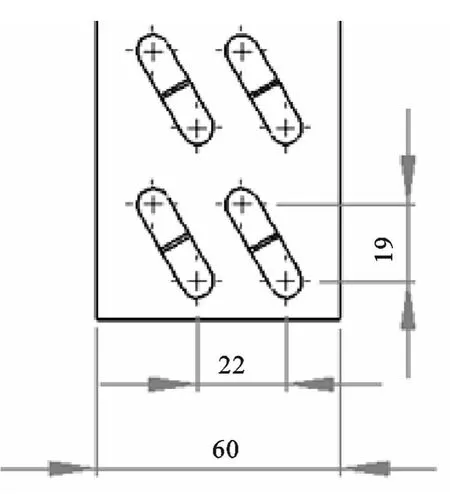
图2 斜排翅片蒸发器的侧视局部图

图3 蒸发器阻力计算模型

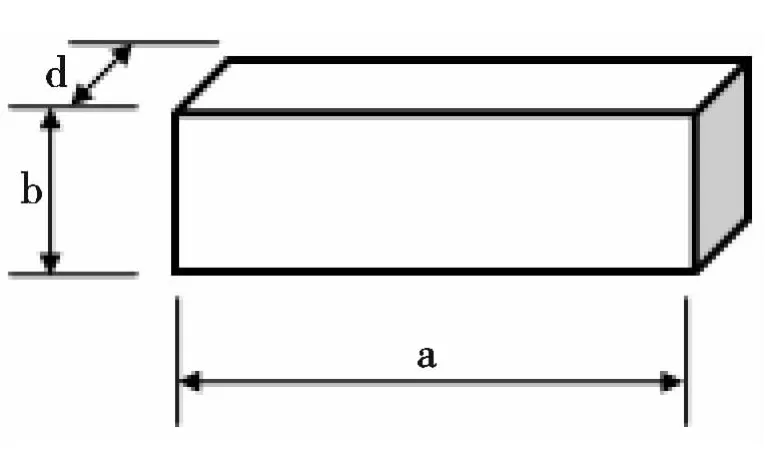
图4 蒸发器通风空间模型

表1 蒸发器的尺寸参数单位:mm

在建立计算模型后，计算出每两管间的阻力值，对于不同管排计算，分别对应于不同的密片管与疏片管的阻力，这样在不同蒸发器中对应的是除管排数不同外，差别关键在于密片的管排数与疏片的管排数。

3 蒸发器阻力计算

通过上面计算模型的建立，针对图3中的模型结构，在计算阻力值时分别按照直线段阻力计算与局部阻力计算，这两种阻力计算分别按照下面的系列公式进行:

3.1 直线段阻力和局部阻力计算公式

上述各式中符号意义:

R—直线段阻力系数，Pa/m;

P1—直线段阻力值，Pa;

P2—局部阻力值，Pa;

λ—摩擦阻力系数;

ρ—空气密度，kg/m3;

v1—无管处翅片流速，m/s;

v2—管间处翅片流速，m/s;

D—当量管直径，m;

ν—空气粘度系数，m2/s;

Re—雷诺数;

ξ—局部阻力系数

在上述的计算公式中，(6)主要是进行局部阻力计算，而其它公式则进行直线段阻力计算。分析目前无霜冰箱的通风量大小，初步计算出雷诺数不超过1000，因此可以判定流过蒸发器翅片中的流体为层流状态，可以选用摩擦阻力系数的计算公式(4)，而(6)中的流速v2主要是根据蒸发器尺寸数据c与a之间的变化影响。对于局部阻力系数目前并没有准确的参数，但针对于此类蒸发器的特点以及模型建立的特点，最后修正此参数，本论文的重点也主要是如何确定局部阻力系数值。

由于蒸发器在实际的过程中是一个非常复杂的状态，通过的空气为湿度较大的低温空气，它的参数是一个不稳态的过程，但为便于研究与对比分析，计算是在常温的状态下进行，也便于与风洞设备的测试参数一致。

3.2 蒸发器模型阻力计算实例

计算时按空气温度在20℃的环境下进行测试，因此空气的粘度系数ν为16×10－6，空气的密度ρ为1.2 kg/m3，通过改变流过蒸发器的不同速度，也就是说当流过蒸发器(V1)的速度不同时，产生的雷诺数也不同，按公式(2)进行计算，可以得出图5的曲线。

通过公式(4)，可以由雷诺数大约求出摩擦阻力系数与蒸发器流速(V1)之间的关系。如图6。

图5 雷诺数与蒸发器流速的关系

图6 摩擦阻力系数与蒸发器流速的关系

根据图3的模型，可以通过公式(6)计算出蒸发管局部阻力变化关系曲线，式中的局部阻力系数ξ是一个关键的参数，无法采用理论计算出来，本文是通过参考文献建立缩口与扩口类似模型计算，得出一个初步值约为0.32，最后通过与实际测量的结果对比进行修正。

通过图4的模型，可以将蒸发器分别建立密片与疏片的模型方式，通过公式(1)和(5)系列计算公式，分别计算出单排管模型的阻力变化关系曲线。

通过系列计算后，单排管段(密片)阻力与速度的关系，如图7。

同样，可以计算出单排管(疏片)蒸发器阻力与流速的关系，如图8。

图7 单排管(密片)阻力与流速的关系

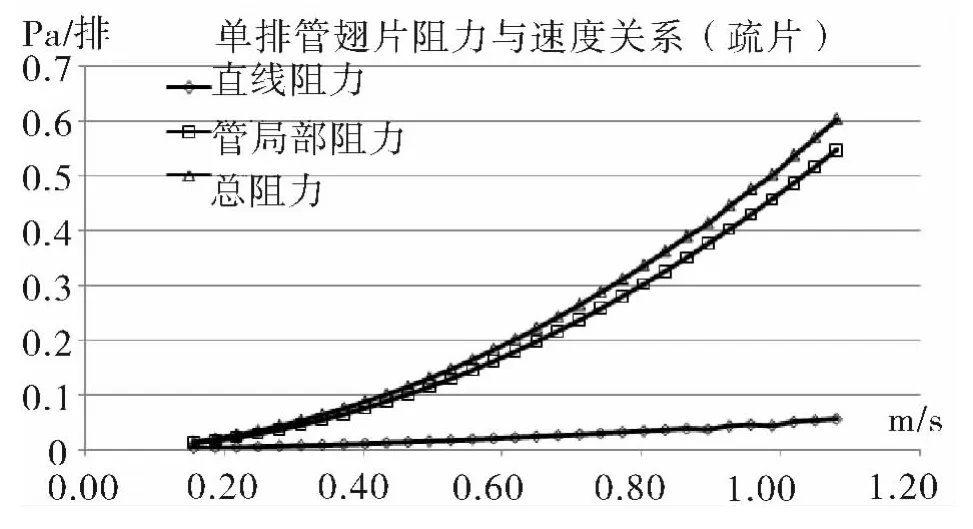
图8 单排管(疏片)阻力与流速的关系

在分别计算出蒸发器单排管的阻力与流速的变化关系后，可以针对不同的蒸发器结构计算出整体蒸发器的阻力与流速的关系。

3.3 蒸发器整体阻力计算

其中:

n1—密片管排数

n2—疏片管排数

P1，P'1—单排管直线段阻力

P2，P'2—单排管局部阻力

另外可以通过曲线求出各阻力的曲线方程。如:

(1)对于密片管总阻力，曲线方程为:

y=0.39x2+0.137x

(2)对于疏片管总阻力，曲线方程为:

y=0.39x2+0.039x

对于完整蒸发器，总的方程也可以表示为:

式中的V1为空气流过蒸发器的速度，但对于一般的设计来说，主要是考虑到通过蒸发器的通风量，在这一点上，通风量与流速主要是与蒸发器的宽度L和深度a尺寸相关，可以通过转化计算出关系式。由于本模型主要是基于a为60mm尺寸的蒸发器设计，所以公式(8)也可用风量Q与蒸发器宽度L来表示，如公式(9)。

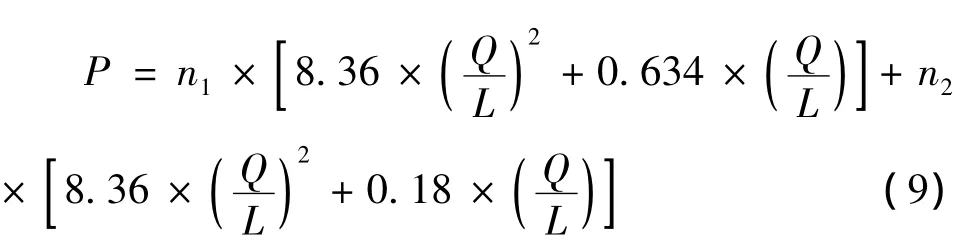
从公式(9)可以看出，蒸发器的阻力主要与风量的变化、蒸发器的宽度、密片管排的数量及疏片管排的数量有关。

4 阻力测试及对比分析

由于在阻力的计算中有许多的经验数据是否准确会影响到计算结果的精度，特别是局部阻力系数是通过经验数据进行选择，它的准确程度会影响计算的结果与实际的偏差，正因为如此，通过风洞试验测试设备对不同蒸发器进行阻力测试，对比两者的结果，并进行修正，可以较好地整理出此类蒸发器阻力的计算值。

图9为蒸发器3的实物图。

三种蒸发器的阻力测试结果如图10。

具体测试数据如表3。

表2 三种蒸发器的结构特征

图9 蒸发器3的实图

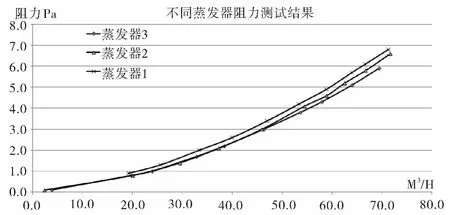
图10 三种蒸发器阻力与风量的关系

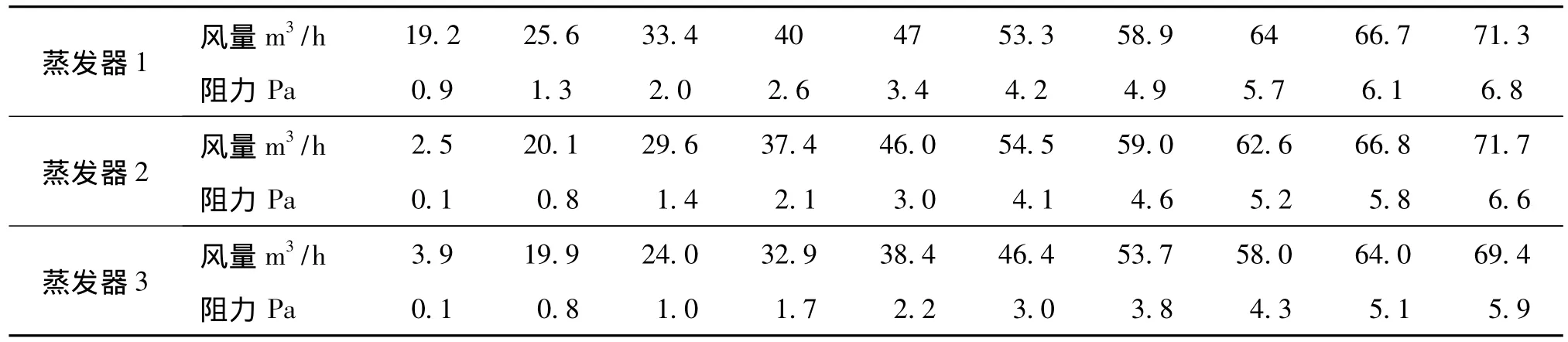
表3 三种蒸发器的阻力测试数据

通过上述模型计算的结果，可以与实际测试的三种蒸发器的阻力测试值进行分别对比。为更准确对比两组数据，对实际测试的结果曲线找出曲线方程，更方便与计算的结果进行对比，对比结果分别如图11，图12，图13。

通过对局部阻力系数ξ的修正，本文选定为0.35后，经过理论计算后与实际测试的结果比较一致，说明计算的方向是正确的，计算的结果可以应用。

图11 蒸发器1的计算结果与实际测试结果对比

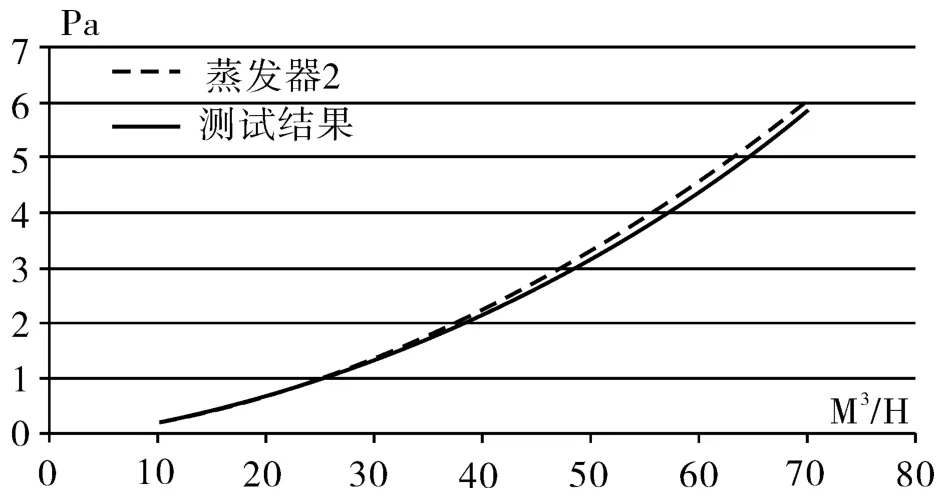
图12 蒸发器2的计算结果与实际测试结果对比

图13 蒸发器3的计算结果与实际测试结果对比

经过上面的对比研究，发现在实际的测量中L的准确度对结果的影响比较大，同时蒸发器两侧的密封性也会影响到测试结果的偏差，在经过更多不同尺寸的蒸发器测试对比后，总的偏差并不大。

从蒸发器阻力的计算公式中可以发现，只需要了解蒸发器的几个关键尺寸后，可以计算出不同风量下的蒸发器阻力，有了这种简单的计算方式后，可以用软件仿真出无霜冰箱的风道阻力与风扇性能参数的匹配，从而可以找出冰箱的工作点。当然这种方式对于冰箱在实际工况下有很大的不同，如空气的参数不同，冰箱的结霜状态不同等，但对于对比分析不同风道系统的好坏是可行的。

5 结论

通过对翅片蒸发器结构的研究，建立简易计算模型，并基于蒸发器的设计变化方式，有利于蒸发器的规格在实际使用中的变化，通过一些固定的尺寸，在可变的结构方面进行模型建立，如蒸发器的宽度、不同翅片的高度等，通过计算后的方程可以较快地分析出新蒸发器的阻力值随风量变化的情况。

通过与实际产品经风洞测试设备对比后，可以对模型计算的结果进行较好的修正，关键是局部阻力系数的修正与确定，使理论计算结果与实际测试结果较好地接近。

通过理论计算与实际测试结果的对比，在风量不大的情况下，两者的结果偏差比较小，说明理论计算的模块化可以对同类型的蒸发器进行分析，尤其与制冷系统的仿真分析结合后，可以更好地动态研究无霜冰箱的风道阻力与风量的变化，从而更好地研究无霜冰箱的性能。

*:本论文所使用的风洞试验设备得到国家技术中心能力建设资金赞助

［1］陈沛霖，岳孝方.空调与制冷技术手册［M］．上海:同济大学出版社，1990，7