受弯构件中表层纵向构造钢筋配筋计算分析*

高明赞 杨新旋(温州路桥工程设计所,浙江 温州 325000)

受弯构件中表层纵向构造钢筋配筋计算分析*

高明赞 杨新旋
(温州路桥工程设计所,浙江 温州 325000)

在钢筋混凝土受弯构件中,受拉区表层钢筋的拉应力比内部大,部分构件因构造需要和施工方便,在受拉区主筋外侧配置纵向构造钢筋。为保证纵向构造钢筋不至应力过大破坏和结构裂缝宽度超限,其钢筋的截面面积需大于最小计算值。主筋外侧纵向构造钢筋的最小截面积与主筋的计算截面积呈正比,并随其与主筋距离的增大而增大。

混凝土结构;构造钢筋;应力;裂缝;配筋

钢筋混凝土结构是世界上使用最为广泛的结构形式之一,普遍应该于桥梁、码头、水库大坝和房屋等工程中。钢筋混凝土构件有受压、受拉和受弯等,对于受弯构件,中和轴的一侧受拉,另一侧则受压,为更好地发挥钢筋和混凝土的优势,需在受拉区配置钢筋,来承担主拉应力。

在荷载作用下,位于受弯构件受拉区的钢筋,越靠近混凝土表面,受到的应力就越大,一般认为钢筋应力与其至结构中和轴的距离呈正比。为了使钢筋混凝土结构能达到最大抗弯承载力,一般受拉区钢筋都配置在靠近结构表面位置,钢筋距混凝土表面以适当的混凝土保护层厚度进行控制。但有些构件因构造需要或方便施工,在主筋外侧还布置了构造钢筋,如桥梁中的L型盖梁。对于这些构件,在结构内力计算时,一般不考虑外侧构造钢筋参与受力计算,仅考虑其控制非荷载裂缝的作用(构造钢筋可以提高混凝土的极限拉伸应变和有效地减小开裂处混凝土的应变集中)[1]。

对于多跨且不等跨的桥梁,因桥墩两侧的桥板高度不同,需要将桥墩盖梁顶顺桥向设计成台阶状(L型盖梁),以使两侧板顶同高(如图1)。桥墩盖梁在配筋计算时,一般不考虑台阶凸起部分,盖梁截面按一般的矩形截面进行计算。盖梁配筋时,在盖梁台阶底布置主要受拉钢筋,台阶凸起部分仅配置构造钢筋。盖梁在荷载作用下,柱顶及附近位置形成负弯矩,盖梁上部为受拉区,台阶表层的构造钢筋应力要比主筋的大。若该位置的纵向构造钢筋截面积过小,其受到的拉应力可能会超过其抗拉极强度,或者造成结构裂缝宽度超限制,影响结构耐久性。*收稿日期:2013-05-24

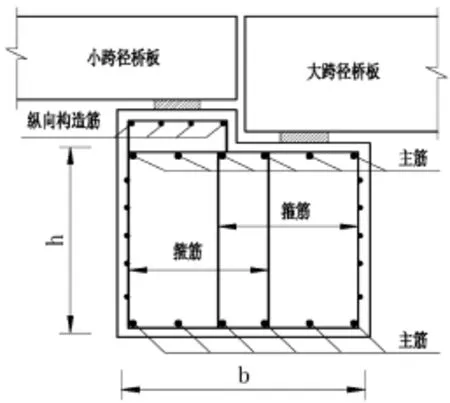
图1 桥墩盖梁横断面

因此,为了避免受拉区主筋外侧纵向构造钢筋不因应力过大而失效和裂缝宽度超限,本文将通过结构受力分析,研究表层纵向构造钢筋应力的影响因素,以及计算其需配置的最小截面面积,为结构设计提供理论参考。

1 计算模型

设一桥墩盖梁高为h,宽为b,为简化计算将盖梁上台阶假设宽为b、高为H的矩形截面。盖梁配筋计算时不考虑台阶截面,其计算模型为图2,并假设计算后的受拉区主筋截面积为AS1(不考虑安全系数)。此时,满足(1)式[2]。

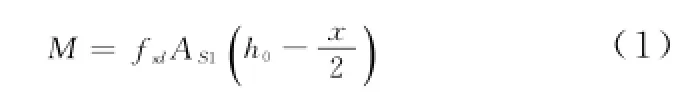
式中:M为该截面的最大弯矩;fsd为主筋抗拉设计强度;x为等待受压混凝土高度。

盖梁主筋配置完成后,在主筋外侧台阶顶配置构造钢筋,设纵向构造钢筋截面面积为AS2,并假定构造钢筋截面面积AS2比主筋的截面面积AS1小得多。在相同的荷载作用下,设受压区混凝土面积x不变(实际工况下会变小,但由于构造钢筋截面面积为AS2比主筋的截面面积AS1小得多,可忽略构造钢筋对等待受压区混凝土高度的影响),见图3。此时,满足(2)式。

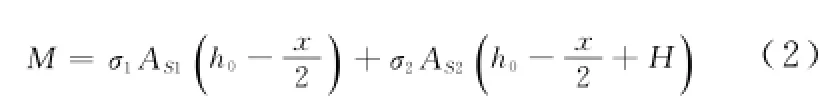
式中:σ1为受拉区主筋的应力;σ2为受拉区主筋外侧纵向构造钢筋的应力。

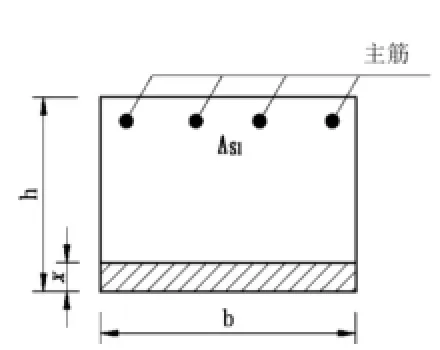
图2盖梁配筋计算截面

图3盖梁工况下计算截面

2 纵向构造钢筋强度计算

2.1 钢筋应力

钢筋的拉应力与其应变量呈正比,对受弯构件而言,结构外边缘变形大于内部,故外围钢筋的拉应力大于内部钢筋的拉应力,即σ2＞σ1。可认为钢筋应力与其至中和轴的距离呈正比,则:

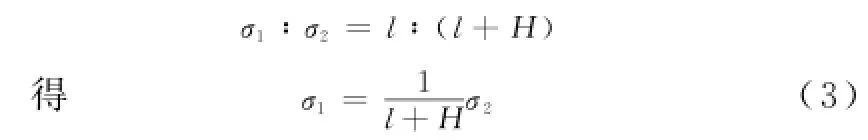
式中:l为主筋至梁中和轴线的距离。将(3)式代入(2)式,得:

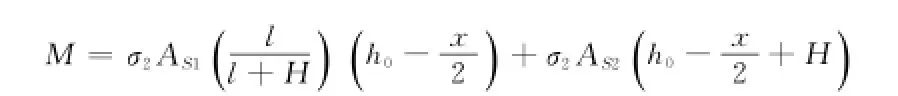
换算得:

在盖梁受到设计最大荷载作用下,其受到的弯矩与原截面设计值相等,则将(1)式代入(4) 式,得(5)式。

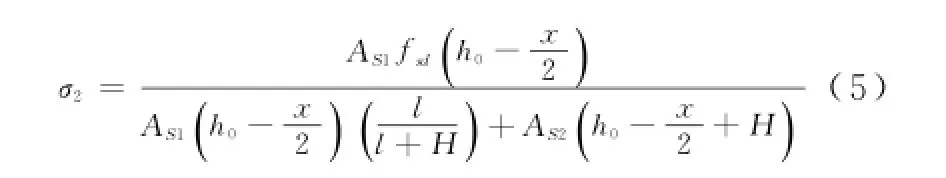
2.2 钢筋最小截面积

随着荷载的增大,受拉区钢筋应力也随之增大,假设侧纵向构造钢筋达到抗拉设计强度值,即σ2=fsd,则:

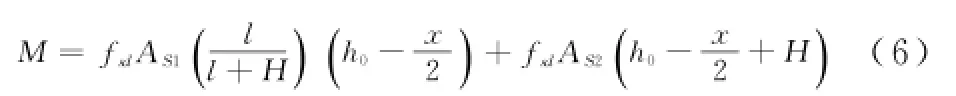
若使结构在最大设计荷载(Mmax)作用下纵向钢筋的应力不超过钢筋的设计强度fsd,则满足(7)式。

3 裂缝宽度计算

3.1 裂缝计算理论

对于一般的受弯或受拉钢筋混凝土构件,在荷载作用下,中和轴的一侧受拉另一侧受压,或全截面受拉,由于混凝土的抗拉强度比抗压强度小得多(约为1/10),当受拉区混凝土受到的主拉应力大于其抗拉强度或主拉应变大于其极限拉伸应变时,会导致受拉区混凝土被拉开,结构就产生裂缝。其实,影响结构裂缝形成的原因比较复杂,影响因数很多,其裂缝宽度计算理论也不统一。目前,钢筋混凝土结构裂缝理论主要有粘结滑移理论、无滑移理论、综合理论和数理统计理论[3]。

我国现行的《混凝土结构设计规范》(GB50010 -2010)、《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD62-2004)等规范都对裂缝宽度提出计算公式。规范GB50010-2010中对矩形、T形、倒T形和I形截面的钢筋混凝土受拉、受弯和偏心受压构件在荷载长期作用下的最大裂缝宽度按(9)式[4]计算:

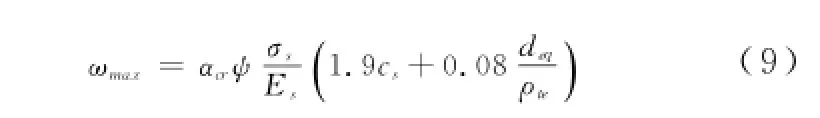
式中:αcr为构件受力特征系数;ψ为裂缝间纵向受拉钢筋应变不均匀系数;σs为受拉区纵向钢筋应力;Es为钢筋的弹性模量;cs为受拉钢筋的混凝土保护层厚度;deq为受拉区纵向钢筋的等效直径;ρte为有效受拉混凝土截面面积计算的纵向受拉钢筋的配筋率。

规范JTGD62-2004中对矩形、T形和I形截面的钢筋混凝土构件及B类预应力混凝土受弯构件的最大裂缝宽度按(10)式[5]计算:

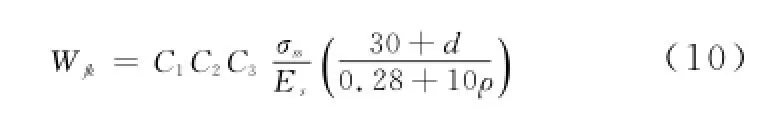
式中:C1为钢筋表面形状系数;C2为作用长期效应影响系数;C3为与构件受力性质系数;σss为钢筋应力;d为纵向受拉区钢筋直径;ρ为纵向受拉钢筋的配筋率。

3.2 钢筋最小截面积

无论采用何种设计规范,为了简化计算,本文仅对受拉区构造钢筋裂缝宽度与原结构进行比较。设原结构按设计规范对结构进行最大裂缝宽度验算合格后,受拉区主筋的截面面积为AS1',受拉区纵向构造钢筋面积为AS2',则满足(11)式。

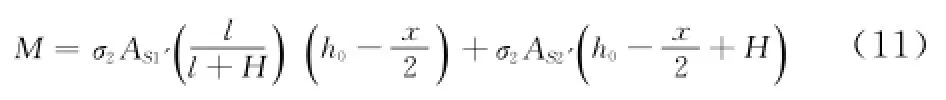
从(9)、(10)式可知,结构裂缝宽度与钢筋应力σ呈正比,当荷载作用达到最大值时,(11)式中纵向构造钢筋σ2也达到最大值。为使受拉区纵向构造钢筋位置最大裂缝宽度不超过规范要求值,则构造钢筋应力需满足(12)式的要求。

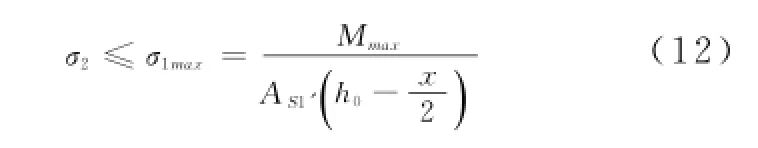
设荷载作用达到最大值(Mmax),以及纵向构造钢筋σ2也达到规范允许的最大值,此时满足(13)式。简化(13)式,得(14)式。

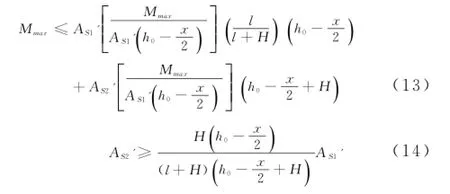
4 计算结果分析

从结构裂缝宽度等计算结果看,(8)式与(14)式相同。纵向构造截面积只要达到最小计算值,构造钢筋就不会因应力过大而失效,同时纵向构造钢筋位置处的裂缝宽度也不会超限。

对于某一结构尺寸和配筋合理的构件,其结构的中和轴至受压区混凝土表面的距离Xc与结构等待受压混凝土高度x呈正比,即满足(15)、(16)式。将上式代入(8)式,得(17)式。

式中:AS2为受拉区表层纵向构造钢筋的截面积(mm2);AS1为受拉区主筋的截面积(mm2); H为受拉区表层纵向构造钢筋至主筋的距离(mm);h0为结构有效高度(仅考虑主筋)(mm); x为等待受压区混凝土高度(mm);β为截面受压区矩形应力图高度与实际受压区高度的比值。

对于某一实际结构,AS1、x和h0为已知常数, 设AS1=a,h0-x/2=b,则得(18)式。通过计算可得,纵向构造钢筋的最小截面面积AS2与其至主筋之间的间距H有关,其变化曲线见图4。图中,a取3000mm2,b取1000mm,l取900mm。

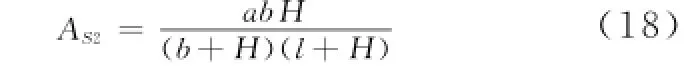
从计算公式及曲线可以看出,为使受拉区主筋外侧纵向构造钢筋应力不超过钢筋的设计抗拉强度和裂缝宽度不超限,构造钢筋截面面积应满足最小值。纵向构造钢筋最小截面面积随其与主筋之间的间距的增大而增加,当增大一定值后,无论H是是否继续增大其都可满足要求。此后,再随着距离的增大,受拉区应力主要由纵向构造钢筋承担。随着H的增大和构造钢筋截面的增加过程中,主筋的应力将不断减小,结构的整体承载力不断提高。

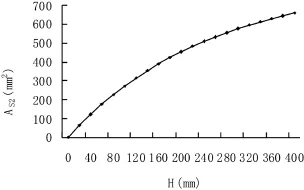
图4 AS2随H的变化曲线

5 案例

某桥梁,桥墩一侧为13m空心板(板高70cm),另一侧为20m空心板(板高95cm),由于两侧桥板高度不同,将桥墩盖梁顶设置成台阶状(L型),13m空心板处台阶高25cm。通过对盖梁进行内力计算,盖梁在负弯矩处(立柱位置)需配置8根直径为22的HRB335钢筋,其总截面积为3041mm2(其中,h0=1150mm,x=30mm,C30混凝土fcd=13.8MPa),为满足构造要求,在台阶顶配置4根直径为12的HRB335钢筋(如图5)。

图5 盖梁横断面配筋图

将以上结果带入(18)式,计算得纵向构造钢筋最小截面积为456mm2(其中,H=250mm,β= 0.8),是受拉区主筋的0.15倍。考虑受拉区主筋的实际配筋比设计值略大,将使受拉区钢筋应力有所减小。故在台阶顶配置4根直径为12的HRB335钢筋(总截面积为452mm2)满足最小截面要求。

6 结语

为保证钢筋混凝土受弯构件受拉区主筋外侧的纵向构造钢筋应力不超过设计抗拉强度,以及结构裂缝宽度不超限,纵向构造钢筋的截面积必须满足最小计算值要求。主筋外侧纵向构造钢筋的最小截面积与主筋计算截面积呈正比(一般是主筋的10-30%),随其与主筋距离的增大而增大,到达一定值后趋向稳定。对于一般的结构,按构造要求配置的构造钢筋截面积基本可以满足最小值要求,无需过分增加。

[1]郑小龙.构造钢筋控制非荷载裂缝产生与发展的机理研究[J].中外建筑,2008,(3):128-130.

[2][3]叶见曙.结构设计原理[M].北京:人民交通出版社, 2005:190-192.

[4]中国建筑科学研究院.GB50010-2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010: 88-90.

[5]中交公路规划设计院.JTGD62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004:60-61.

TU375

B

1672-9846(2013)02-0071-04

高明赞(1987-),男,浙江瑞安人,温州路桥工程设计所助理工程师,主要从事公路桥梁设计和混凝土结构耐久性研究。

杨新旋(1985-),男,浙江瑞安人,温州路桥工程设计所助理工程师,主要从事公路桥梁设计研究。