正交各向异性新模型在平面应力问题中的应用

柯 江

(陕西理工学院土建学院，陕西 汉中 723001)

0 引言

固体材料一般是各向异性的，例如木材、岩石、复合材料等，但为了简化分析，一般把固体材料简化为各向同性、横观各向同性与正交各向异性。目前，各向异性弹性力学问题的计算方法有解析法与数值解法两大类，但这些计算方法都非常复杂[1]。笔者在文献[2]提出了一种线弹性的正交各向异性新单元模型，而在文献[3]中的新单元模型是文献[2]中新单元模型的特例;在文献[4][5]又把新单元模型推广到各向同性与正交各向异性的理想弹塑性材料，并且给出了利用新单元求解固体受外力作用而发生的位移、应变及应力的方法。对于一个平面应力问题，本文将利用新单元法来求解，并与有限元法进行对比分析。

1 计算模型

一个简支深梁(见图1)，长度L=16 mm，高度H=16 mm，厚度t=1 mm，在顶边的中点承受竖直向下的集中力F=300 N，弹性模量 E1=1 ×104N/mm2，E2=2 ×104N/mm2，泊松比 v12=0.8，剪切模量G12=11765 N/mm2。

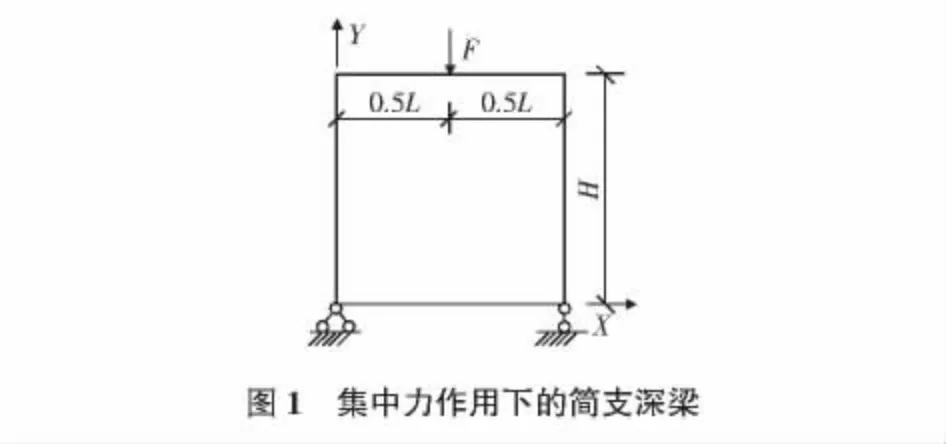
新单元组成的桁架结构计算模型一共包含256个新单元，新单元在X，Y方向的尺寸均为1 mm，三种杆件的截面面积分别为:A1=0.14706 mm2，A2=0.88235 mm2，A3=1.6638 mm2。有限元计算模型采用平面应力单元，单元尺寸与新单元相同，由256个平面应力单元组成。

2 新单元法与有限元法的计算对比

基于Abaqus软件分别采用新单元模型与平面应力单元模型计算该简支深梁，得到的简支深梁位移等值线如图2，图3所示，得到两种方法的计算结果见表1～表5。

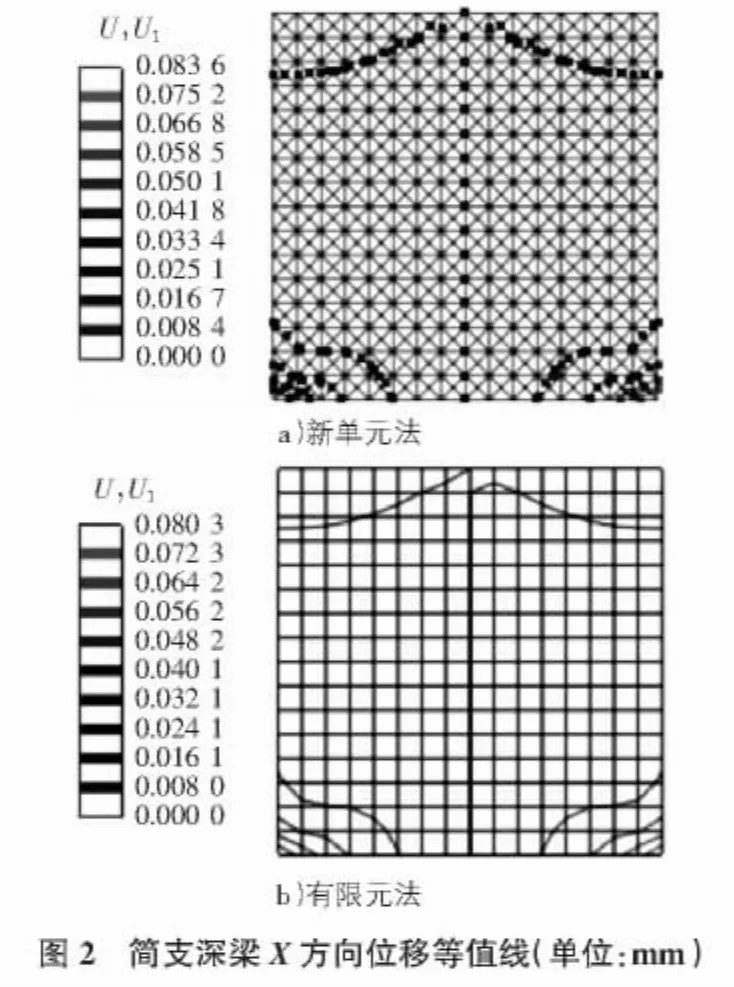
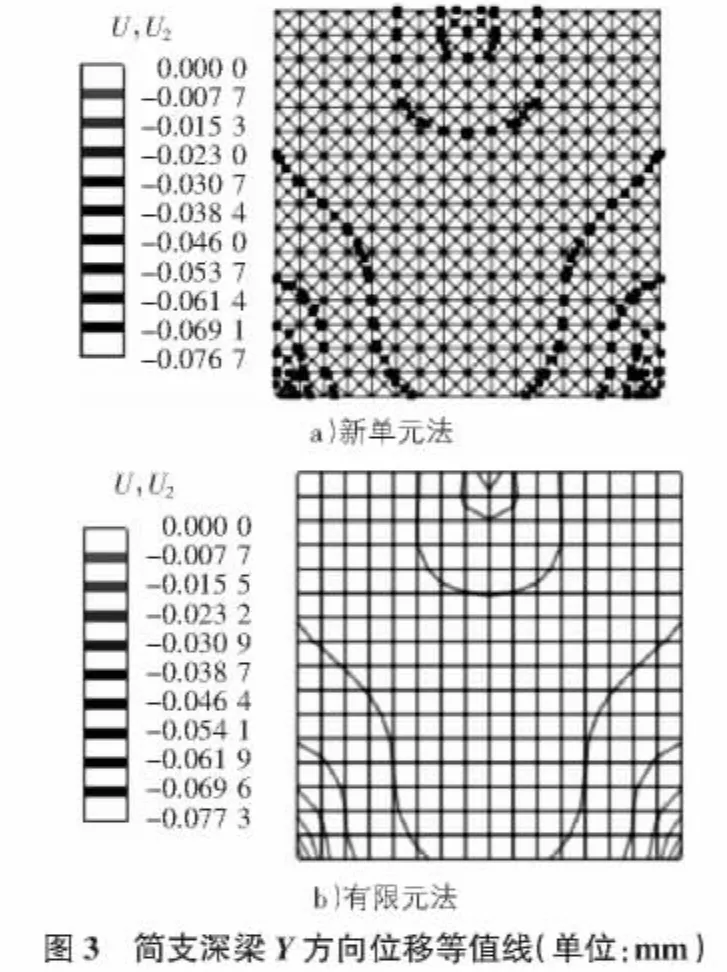
由图2，图3可知，新单元法与有限元法得到的简支深梁位移等值线非常吻合。

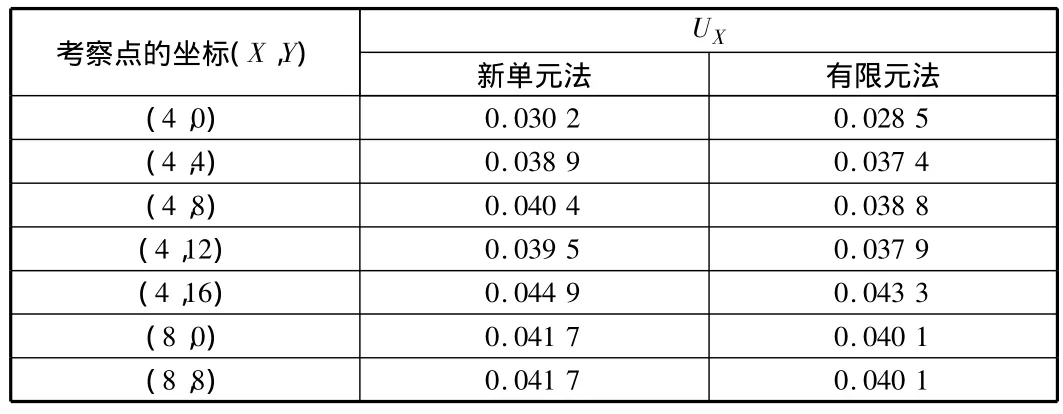
表1 两种方法的X方向位移对比 mm

由表1～表5可知，在边界点和荷载作用点，新单元法与有限元法的结果偏差较大;而在离开边界点和荷载作用点稍远的地方，两种方法的计算结果吻合良好。

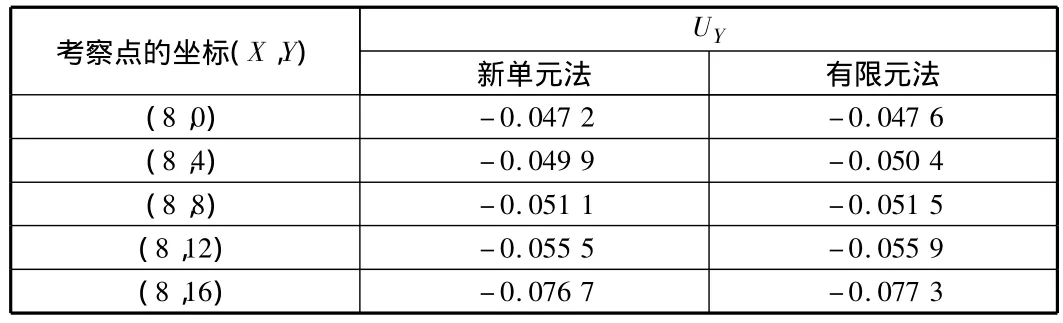
表2 两种方法的Y方向位移对比 mm

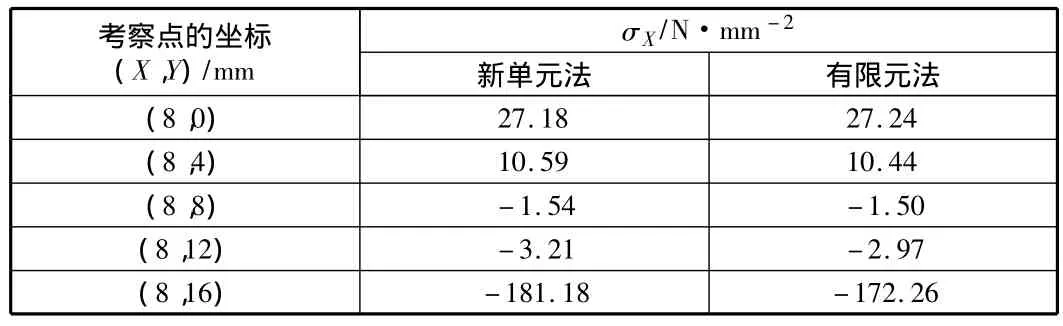
表3 两种方法的正应力σX对比

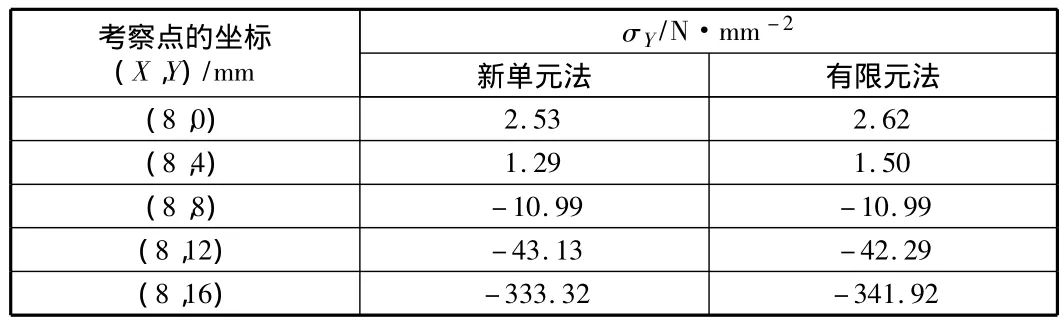
表4 两种方法的正应力σY对比

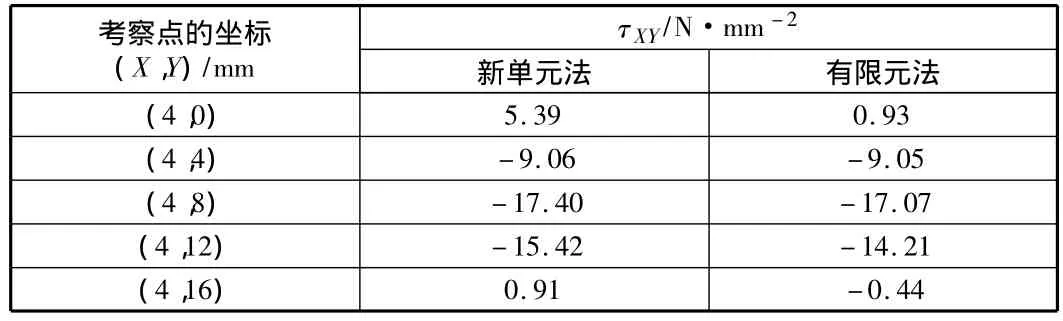
表5 两种方法的剪应力τXY对比

3 结语

根据正交各向异性的固体新单元模型(各向同性、横观各向同性材料是正交各向异性材料的特例)，采用任何一个计算桁架结构的程序就可以非常容易的求解弹性力学问题，与有限元法的计算结果吻合良好，而且当新单元尺寸趋于0时，通过新单元法计算的弹性体的位移、应变及应力趋于精确解。

[1]沈观林，胡更开.复合材料力学[M].北京:清华大学出版社，2006.

[2]KE Jiang.A New Model of Orthotropic Bodies[C].Applied Mechanics and Materials，2012:204-208，4418-4421.

[3]柯 江.弹性固体的新单元模型[J].山西建筑，2012，38(19):58-59.

[4]柯 江.基于固体新单元模型分析理想弹塑性问题[J].山西建筑，2012，38(36):42-43.

[5]KE Jiang.Applications of a New Element Model of Solid Bodiesin Plasticity[C].Advanced Materials Research，2013:690-693，1800-1805.