基于FLUENT的急流槽消能池消能率分析
林云青
(深圳市城市交通规划设计研究中心有限公司,广东 深圳 518000)
0 引言
在山区修建公路,坡面排水是路堑或路堤边坡上方自然坡面排水中的重要组成部分,由于自然坡度通常较陡,雨水经坡面流入坡底截水沟的流速较高,如果消能设施设置不当,水流有可能跃入路面或对坡角及截水沟产生一定损坏。因此有必要设置消能设施来降低流速,急流槽消能池是较常用的公路坡面排水消能设施,但消能池工程应用方面较为缺乏尺寸设计依据。
计算流体动力学(CFD)软件的出现和广泛应用,为公路排水设计的研究提供了新的思路和更先进的研究手段。文章通过CFD软件对急流槽消能池三维模型进行明渠流模拟,对其消能效果进行分析,总结其消能规律,研究结果为急流槽消能池的设计提供参考。
1 消能率
消能率是用来衡量消能设施的消能效果的参数,其大小代表的是流出消能设施的水体的总能量与进入消能设施的流体的总能量的比值的大小。某消能设施的消能率η的值越大,代表该消能设施的消能效果越明显。消能率η的计算公式如下:

式中:Z1——上游相对于下游的高度,m;
h1、h2——上、下游水深,m;
v1、v2——上游进口和下游出口的流速,m/s;
α1和α2——上下游的流速系数,均取1。
2 急流槽消能设施及消能率影响因素分析
2.1 急流槽消能设施
常用的急流槽消能设施为消能池,又称斜插式消能池,通常设置在急流槽末端,在渠底设置抬高的横槛。水流顺急流槽流下时,在一定的池长和横槛高度条件下水位升高,形成水跃以达到消能的目的。
从相关的急流槽消能池的消能率所作的定量分析可知,消能率η是池长l、进口流速ν1、横槛高度及入水角is的函数,可表示成如下形式:

通过同济大学李志勇博士的相关论文数据分析,采用不同的池长l及入水角is时,消能率的变化规律受流速影响不大,可作为单独变量提出。因此消能率η可写成如下形式:

式中:β1——与池长有关的修正系数;
β2——与入水角有关的修正系数;
η′——与流速及横槛高度有关的消能率。
2.2 消能率影响因素分析
影响急流槽消能池消能率的主要因素有进口流速v、急流槽池长l、横槛高度c等。
2.2.1 进口流速(v)
进口流速是影响消能槽消能率的一个重要因素,其大小与某地区的降水强度、进水口的水体高度有关系,在讨论消能率与设计径流量的关系时,将进口的水体深度设为定值,以进口流速作为自变量,分别讨论当水体的流速为3m/s、4m/s、5m/s时的消能池消能率情况。
2.2.2 急流槽池长(l)
急流槽池长l为图中所示消能池的底边长度,消能池池长是影响消能率的一个重要因素(如图1所示)。消能池池长越大,单位宽度池中坡顶流入的水体在槽中所停留的水量就越大,因此直观推理应可知消能率将越大。本论文所设计的模型的急流槽池长分别为2m、3m,并对仿真结果进行分析。

图1 急流槽池长与横槛高度示意图
2.2.3 横槛高度(c)
横槛高度为图1中所示消能池的横槛高度c。消能池池高是影响消能率的另一个重要因素,因此横槛高度应保证水体进入急流槽能引起水跃发生,以达到消能的目的。
消能池横槛高度越大,流入池中水体的水跃作用就越明显,因此可知消能效果就越明显,但横槛高度与路面的高程有关,过高的横槛高度在公路工程中也不适用。本论文所设计的模型的急流槽横槛高度分别为0.3m、0.4m,并将仿真结果进行分析。
3 Gambit三维模型
用Gambit建立了坡度is分别为1∶1、1∶1.5的两个三维模型。
图2为急流槽消能设施的二维计算模型示意图,图3为其对应的三维计算模型示意图。进口边界由上部的气体进口(inletA)和的水进口(inletW)组成。水进口采用速度进口(velocity-inlet)作用边界条件;所有气体进口都定义为压力进口(pressure-inlet),此边界条件适用于边界压力大小已经确定,但边界上通量未知的情况。设气体边界处的压力都为大气压;出口定义为压力出口(pressure-outlet),由于出口的水流为自由出流,与大气相通,认为出口压力为大气压的值。
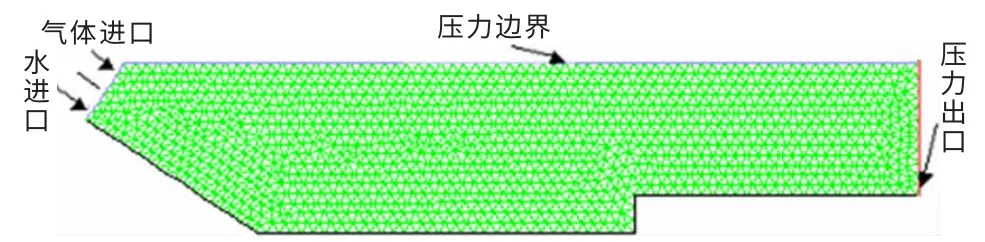
图2 急流槽消能池二维计算模型示意图

图3 急流槽消能池三维计算模型示意图
整个模型就只有一个出口,只能作为同一出口边界,采用压力边界较为合适,一方面气体可以任意流动,另一方面水可以自由出流。
4 计算结果分析
4.1 入水角1∶1.5模型
分析坡度为is=1∶1.5(即入水角为1∶1.5)的急流槽消能模型模拟结果。
水体由上部的进水口以高度0.2m,流体分别以流速为3m/s、4m/s、5m/s的速度进入急流槽消能模型,根椐公式(1),可计算得流体的初始能量。
在对急流槽进行仿真模拟的时候,急流槽的池长分别设计为2m、3m,对横槛高度分别设计为0.3m、0.4m。
将仿真计算得到的出口水流速与消能率列于表1。

表1 消能池消能率计算结果表(入水角为1∶1.5)
通过Fluent迭代近3000次左右以后,模型出口(包括气体和液体)的平均流速已经达到定值,计算结果已经收敛。再对整个模型内的水流速度进行等值着色处理,可以看到水跃发生的位置以及水跃高度和进水口水流的流速有较大的关系(如图4所示),并且水体进入急流槽的速度越大,则产生水跃的地点距进水口越远,即产生水跃越晚,同时水跃的高度越低,即横槛对水流的消能作用越明显。
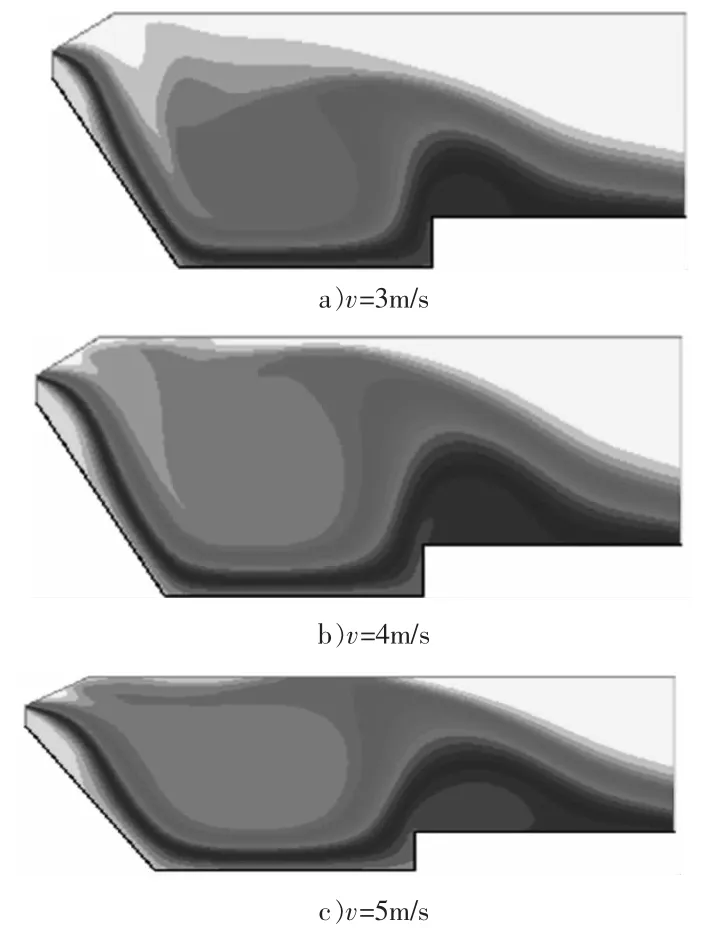
图4 不同流速下自由水面示意图
4.2 入水角1∶1模型
首先分析坡度为is=1∶1的阶梯消能模型。
水体由上部的进水口以高度0.2m,流体分别以流速为3m/s、4m/s、5m/s的速度进入急流槽消能模型,根椐公式(1),可计算得流体的初始能量。
在对急流槽进行仿真模拟的时候,急流槽的池长分别设计为2m、3m,对横槛高度分别设计为0.3m、0.4m。
将仿真计算得到的出口水流速与消能率列于表2。

表2 消能池消能率计算结果表(入水角为1∶1)
4.3 结果分析
对急流槽消能池的消能率作定量分析可知,消能率η是池长l、进口流速ν1、横槛高度c及入水角is的函数,可表示成式(4)的形式。下面对其中的进水口的水体速度v和急流槽的池长l进行定量分析。
4.3.1 进口速度v
在模型进水口坡度、急流槽横槛高度、池长分别设定为定值1∶1、0.4m、2m的情况下分析消能池消能率与进口速度v的关系,如表3所示。

表3 急流槽消能率与进水口速度的关系表
从图5可以看出,当进水口速度在一定范围内变化时,急流槽的消能率随着进口的水体速度变大而变大。

图5 急流槽消能率与进水口速度关系图
4.3.2 池长l
在模型进水口坡度、急流槽横槛高度、进水口速度分别设定为定值:1∶1、0.4m、3m/s的情况下分析消能池消能率与池长l的关系见表4。

表4 急流槽消能率与急流槽池长的关系表
从图6可以看出,当急流槽池长在一定范围内变化时,急流槽的消能率随着急流槽池长的变大而变大。

图6 急流槽消能率与急流槽池长关系图
5 结论
5.1 对急流槽消能池的设计,首先应保证在跌水池内水流形成水跃,根据本文计算结果分析,即应满足消能率随进口流速的增加而增加,如出现降低的现象,则说明水跃没有形成或水跃不足;若进口流速过大,导致消能后出口流速仍较大时,可采取在池内设置横槛的方法来增加消能效果。
5.2 本文对急流槽的消能池进行了三维建模计算分析,完善了二维模型中忽略的边壁粗糙对水流横向速度分布的影响,但是消能槽的宽度对消能率的影响还有待于作者及相关的研究者进一步研究。
5.3 由于三维建模及计算的复杂性,本文对提及的自变量未进行足够多的仿真计算,样本容量较小,不足以对相应的自变量进行数学建模,对急流槽消能池的设计参考帮助有限,还有待于作者及相关的研究者进一步研究。
[1]JTJ 018—97,公路排水设计规范[S].
[2]谈至明.公路截水沟设计和典型结构[J].公路交通科技,2005,(5):43-46.
[3]谈至明.公路急流槽管的典型结构[J].公路交通科技,2005,(6):60-64.
[4]李志勇.路表排水计算理论及设计方法的研究[D].上海:同济大学,2006.
[5]杜平安.有限元网格划分的基本原则[J].机械设计与制造,2000,(1):1-4.

