大规模互联网推荐系统优化算法＊

姜 鹏，许 峰，周文欢

（河海大学计算机与信息学院，江苏 南京 211100）

1 引言

如今人们的生活、工作、娱乐都离不开互联网，互联网也为人们提供了极其丰富的信息和资源。互联网的用户不断地增加，Web 信息也随之成几何级数地增长。这些海量的信息，使用户无法在第一时刻找到自己最想要的资源，这就是“信息过载”所造成的“信息迷向”的现象。推荐系统[1，2.则可以有效地缓解此类问题。

推荐系统根据用户的相关行为构造用户与项目之间的二元关系模型，对冗杂的互联网信息进行过滤和筛选，并将结果推荐给用户。目前，一些电子商务网站（如Amazon、Taobao 等）、搜索引擎（如Google、百度等）、社交网站（如Facebook、豆瓣）甚至微博（如Twitter、新浪微博）都不同程度使用到推荐系统[3]。

推荐系统利用其在互联网信息推荐方面的优势快速发展。早在2000 年，Haubl与Trifts[4]在研究电子商务系统时发现，93%的消费者选择购买推荐系统提供的商品，而此前，能够购买到高质量产品的消费者仅有65%。不仅如此，在另外一些在线商店中，用户的购买行为往往并非事先计划（如图书、音乐、电影等）。此时，一个好的推荐系统，不仅能向用户有效传达最新商品信息，而且可以勾起消费者的购买欲望，推动产业发展。推荐系统会在用户与商品间建立好桥梁关系，用户也会对推荐系统产生依赖。

本文第2节介绍推荐系统研究现状；第3节介绍相似度计算方法；第4节介绍网络的分割规则，并给出SCSG 算法流程；第5节是实验仿真及结果对比；最后给出全文总结。

2 研究现状

可以认为，推荐系统是由智能检索、预测理论等发展而来的，其核心部分为推荐引擎。推荐引擎算法的优劣直接影响到推荐系统的性能[2]。一般地，推荐引擎分为三类，一类是协同过滤推荐（Collaborative Filtering），另一类是内容分析（Content-Based），最后一类是混合推荐（Hybrid）[5]。协同过滤的主要思想是根据用户在系统中的行为（通常为评级操作）计算用户间的相似性，进而根据其“相似用户”的行为预测目标用户的潜在偏好；而内容分析的主要思想是根据用户之前对某些内容的行为，推测用户对相似内容的行为；混合推荐则针对单一推荐的不足，按照不同的策略进行预测。协同过滤的运行效率取决于场景是否满足如下假设：若用户对一些内容的行为相似，则他们对其他内容的行为也大致相似。在古希腊，有这样一句谚语：“观其友，知其人”，在中国也有“近朱者赤，近墨者黑”的俗语。可见在大部分场景中，如Grundy、Amazon等，这个假设基本成立。

随着推荐系统中用户和内容的不断扩充，用户的行为数据将出现极端稀疏性[6]，不仅降低了系统的推荐质量，同时大大降低了算法的运行效率。

文献[7]通过对用户未知评分的项目的预测来降低稀疏性，但评分预测的正确性难以保证，需要大量有效数据进行训练。文献[8]通过单值分解的方式降低项目空间维数，而降低维数导致部分有效数据丢失，难以保证推荐效果。文献[9]通过项目分类信息，采用修正的条件概率方法计算项目相似性，同时通过预测降低稀疏性，从而提高推荐质量。但在问题复杂度上并未做任何优化，过多的预测值也制约着算法的可信度。

本文在上述改进的协同过滤算法的基础上，针对大规模网络环境的特征，设计了一种对网络的合理分割与分组的用户相似度计算方法SCSG（Similarity Calculate method based on Segmentation and Group，下文简称SCSG 算法），该方法能有效降低算法规模，同时缓解网络稀疏性。

3 相似度计算

相似度计算算法是推荐系统中最核心的算法。相似度用于比较两个用户行为的相近程度。通常相似度没有固定或者完全准确的值，在不同的环境中，相似度应当有相对较为合理的一个计算公式。

习惯上，相似度通常满足如下三个条件（这里使用Sim（α，β）表示用户α和β 之间的相似度）：

（1）Sim（α，β）∈[0，1]，且相似度越高取值越接近1。

（2）Sim（α，α）＝1，即行为完全相同的用户相似度为1。

（3）Sim（α，β）＝Sim（β，α），相似度具有无向性。

可见，相似度在性质上与距离十分相似，故相似度的计算通常与距离的计算有一定的关系。

定义1 用户特征向量pα为在某系统中用户a 在n 维项目空间中的所有评分组成的向量。用户a对项目i的评分用rα，i表示，用户α 的特征向量表示为：

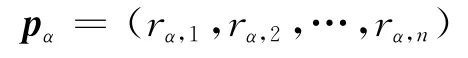
用户特征向量在一定程度上可以反映该用户对所有项目的喜好程度。但是，不同用户之间对项目评分有不同尺度，为改善这种缺陷，引入用户特征修正向量。

定义2 用户特征修正向量是用户的各评分减去用户评分的平均分。用户a 的修正向量表示为：

用户相似性的计算方法常见的有三种：

（1）余弦法：用两个用户的用户特征向量间的余弦夹角表示。

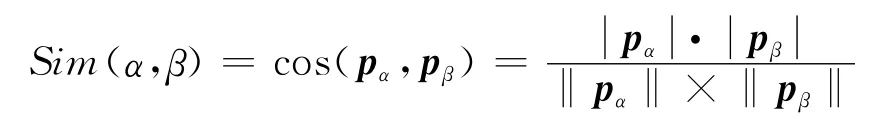
该方法可以度量用户间的相似度，但用户特征向量未考虑到用户的评分特性。

（2）修正余弦法：考虑到不同用户间对评分存在偏好，使用修正特征向量的余弦夹角表示相似度。

令Iα表示用户α 的所有评分项，令Iαβ表示用户α和β共同评分项，rα，c表示用户α对项目c的评分，rβ，c表示用户β 对项目c 的评分，对上式展开后为：

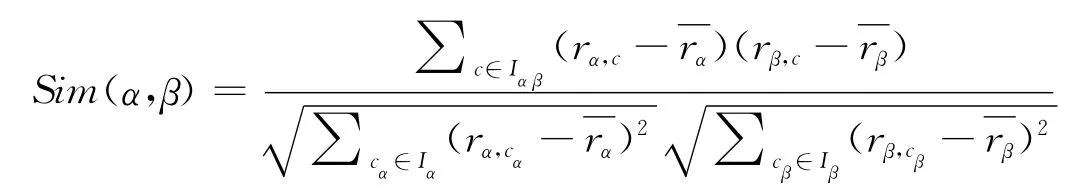
修正特征向量减去了用户对项目的平均评分，该方法则更多体现了用户间的相关性。

（3）相关相似性法：修正余弦法是对两个用户的所有评分项进行计算，而判断用户间的相似性更应该关心用户共同评分项。相关相似法的计算方法为：

若用户α和β间存在关系Iα＝Iβ，则相关相似性法与修正余弦法等价。该算法能够较好地体现用户的相似度，但在大规模的互联网应用系统中，共同评分数据将出现极端稀疏性，影响相似度计算与算法效率。

可见，在大规模的应用场景中，传统的相似度算法存在极端稀疏性，对此文献[7]提出对未知项目的评分进行预测，在一定程度上缓解了该问题。但是，预测值与实际情况难免存在误差，这制约着预测算法的可信度。为避免出现上述情况，本文提出一种SCSG 算法，该算法通过对网络的分割与分组，降低分割后每组网络的稀疏程度，使得在分割后的组间计算相似度不出现极端稀疏现象。同时，分割后的网络规模大大降低，提高了算法的运行效率。

4 分割算法

4.1 传统解决稀疏性方法

目前，解决用户-项目稀疏性的方法主要有以下两种：

（1）矩阵填充技术。该方法旨在通过增加数据来缓解稀疏性。最简单的填充方法为固定值填充，而不同用户的评分一般不同，用固定值不符合实际情况，容易导致相似性失真。文献[10]提出基于BP神经网络的内容预测算法，该算法利用神经网络的学习能力对未知值进行预测，具有一定的可靠性。

（2）矩阵降维技术。文献[9，11]提出一种奇异值分解的降维技术，它将m＊n 的矩阵分解为三个大小分别为m＊m、m＊n、n＊n 的矩阵，然后将分解后的矩阵进行降维处理。降维不仅使稀疏性问题得到解决，还降低了算法的复杂度。

上述两种方法应用在大规模网络中存在一些问题，即忽略了算法预处理的复杂度：在基于BP神经网络的预测值填充方法中，很明显，计算预测值的复杂度较高，通常网络规模越大，矩阵的稀疏性越明显，则要预测的值也非常多，在预测这一步骤中会消耗大量资源。同时，预测值终究不是确定值，在使用时难免出现误差；而降维的方法，虽然表面上最终的计算量是减少了，但为了缓解降维时的信息丢失，在处理时需要通过选取合适的维度k，枚举k的过程会造成较多的时间消耗。

在大规模网络系统环境中，上述方法的预处理时间将会无法承受，直接影响相似度计算的效率。不难发现，上述算法在最终计算相似度时，数据集仍然为全部数据，这在网络数据量很大时，计算时间将无法承受。

4.2 网络分割

4.2.1 大规模网络特征

网络系统的数据量虽然制约着一些算法的实现，但通过分析不难发现，网络具有一些其他性质：

（1）网络数据过多，存在相当一部分无效数据。这些数据在相似度计算时有负作用。

（2）网络数据多，在分析时即使丢失一些有效值，对结论的影响不明显。

（3）网络数据庞大、随机且复杂，这使得全网络的某些特性不如某些子网的特征明显。例如，分析学校学生的特性，以全校学生作为研究对象，得到的特征将会比较少，且大众化，但若根据学院、性别等分别分析，得到的特征将更具有代表性。

从上面的特征可以看出，针对大规模网络的分析，在不影响结论的前提下，对网络进行合适的分割将会得到不错的效果。

4.2.2 二分图建立

定义3 用户-项目图Gu-i＝Vu∪Vi∪Er，其中，Vu为用户顶点集，Vi为项目顶点集，Er为评分边集。

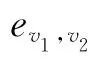
所以用户-项目图是一个二分图。

由于计算相似度时涉及矩阵运算，采用邻接矩阵保存该图。

4.2.3 图的分割

将所有数据保存到一个图结构中，该图必然相当庞大，不便于计算和分析。根据4.2.1节给出的大规模网络特征，本节设计并给出以下四种分割规则，同时给出每种分割规则的算法描述与详细流程。

这里以用户u 为计算目标用户，数据源为MovieLens给出的数据。

（1）连通分组。找到被预测用户u的一个连通二分图Gu。

连通分组剔除了与待测用户毫无交集的用户与项目集。由于是根据连通性分组的，这些被剔除的用户-项目对预测结果的影响将非常小。

求连通图的过程类似于对图的染色，建立用户-项目二分图，利用FloodFill算法对用户u 进行染色。

不难发现，使用FloodFill直接进行递归，将进行多次迭代，导致栈溢出。在递归时限制递归深度，防止算法执行时过分盲目递归。

具体步骤如算法1所示。

算法1 连通分组算法UnionGroup（long Uid）

输入：用户u（Uid）。

输出：连通二分图Gu。

算法描述：计算包含用户u的连通子图。

在实际数据测试时发现，采用完全连通分量，最终得到的结果与原图几乎一样，这样不仅浪费了计算连通分量的时间，还未起到分割的作用。

不同的连通深度，在不同数据量下的分割情况如图1所示。实验数据表明，当递归深度在3以上时，子图的规模大概为原图的80%～90%，且随着深度递增；而当深度大于6 时，规模接近100%。该实验数据与“六度分离”理论不谋而合。

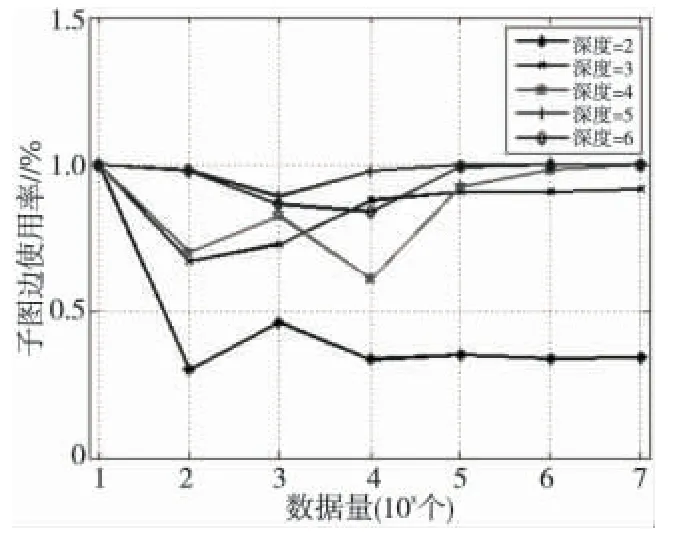
Figure 1 Divided connected subgraph图1 分割连通子图

考虑到分割的效率，最终使用的深度为3。

具体步骤如算法2所示。

算法2 常规分割算法NormalR（Group Gu）

输入：连通二分图Gu。

算法描述：删除常规项，并得到连通子图。

在实际应用中，常规项的选取将直接决定分割的实用效果，应该由专用的数据挖掘系统给出，本文对此不作详细讨论。本文在实验时采用的是选择在边中出现频率最高的项代替常规项。

不同数据规模下，删除多个常规项的分割结果如图2所示。

根据实验结果可知，前两种算法适合数据量相对较小的网络，随着网络的增大，对网络微量的修改无法起到关键作用。

（3）无效项分割。若计算用户u 对项目i 的一个预测评分，且i不属于常规项。根据有效数据优先原则，删除对i项目无评价的用户，并进一步连通分组。

Figure 2 General items divided subgraph图2 常规项分割子图

详细步骤由算法3给出。

算法描述：删除无效项，并得到连通子图。

该分割策略带有一定随机性，由于无效项的删除直接导致用户数的减少，网络的规模也随之减少。根据实验数据，平均的数据减少量可达30%。

（4）项目分类分割。

项目分类分割是在矩阵规模较大时设计的一种根据项目分类信息进行分割的分治算法。

由于有些项目可能有多种分组，在实际计算时需要对每个组分别进行相似度计算。

具体步骤如算法4所示。

算法描述：针对待预测项，对连通二分图进行分类，并分组计算相似性。

项目分组分割可以将求解规模较大的矩阵分解为多个规模很小的矩阵间的运算，大大提升了相似度计算的效率。同时，采用同类不同种的项目的评分作为相似度的判定标准，在实际应用场景中较不分组的方法，更具实际意义。

4.3 改进的协同过滤算法

4.2 节简要叙述了网络分割对运算复杂性的影响，同时给出了四种网络分割算法，并分析了每种分割算法的特点。本节给出结合上述网络分割的相似度计算流程。

相似度计算的最终结果为相似度矩阵。

定义4 用户-项目相关相似度矩阵为：

其中Simi（α，β）表示α与β关于项目i之间的相似度。

计算组内预测值的公式如下（用户Uid 对项目Iid 的预测评分）[12]：

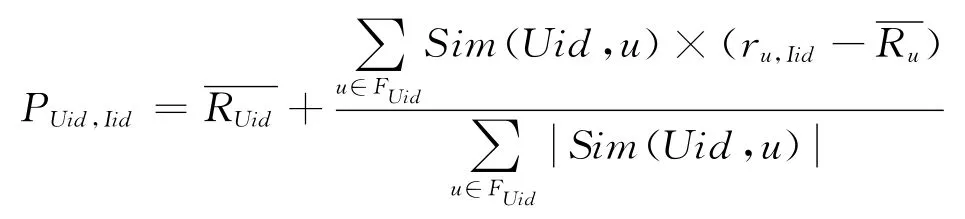
其中FUid＝｛F1，F2，…，Fn｝为用户u的组内最近邻居集。

具体步骤如算法5所示。

算法5 SCSG 算法SCSGCalcuSim（long Uid）

输入：系统数据集DataSet，用户编号Uid。

输出：用户的前10个推荐项目。

算法描述：生成用户关于项目i的相关相似度矩阵。

5 实验结果

本文的所有实验数据均使用MovieLens网站公布的大规模数据测试集，同时MovieLens自身也是一个互联网推荐系统。该测试样例包含10 000 054项评分记录、95 580个标签、10 681部影片、71 567名用户。为验证计算结果的准确性，将评分数据的90%作为训练数据，10%作为测试数据。

平均绝对偏差MAE（Mean Absolute Error）是常用的衡量推荐系统推荐质量的评价指标之一[13]。MAE 的计算方法如下所示：

本节使用MAE 作为指标，将对SCSG 的协同过滤法与传统的余弦、基于修正数据的协同过滤法进行比较，判断推荐质量；使用算法运行时间作为指标判断算法运行效率。

为测试算法运行效率，在测试数据中抽取20组样例数据，分别使用传统协同过滤法、修正协同过滤法和SCSG 协同过滤法进行测试。测试结果如图3和图4所示。

从图3中可以明显看出，在推荐优劣程度上，SCSG 算法较传统的协同过滤算法相似，MAE 略低于其他算法，原因主要在于对项目分组之后使得用户之间的相似关系更加明显。

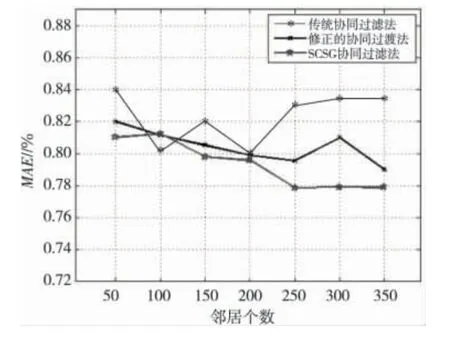
Figure 3 Change of MAE with the number of neighbors图3 MAE 随邻居个数变化图

从图4中可以看出，SCSG 算法的效率明显优于传统的协同过滤算法。

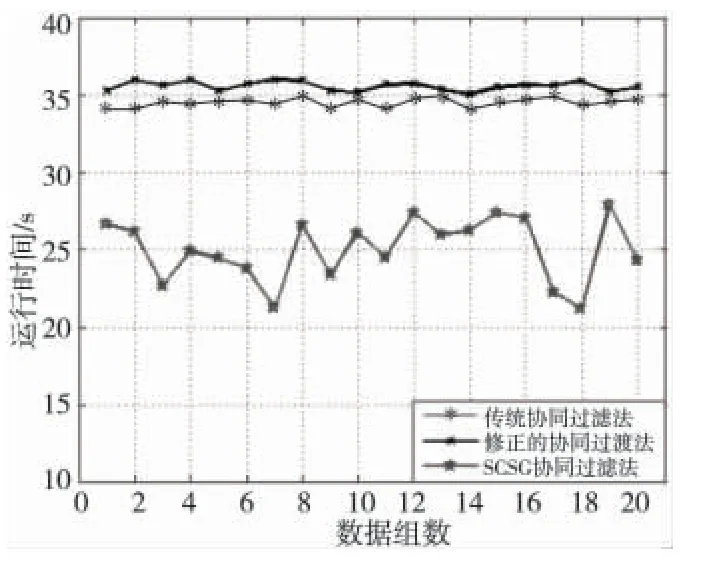
Figure 4 Comparison of running time图4 运行时间对比图

可见，本文提出的算法在效率上较传统的算法有明显的提高，在推荐质量上与传统的推荐算法相似，效率上的提升使得该算法可以应用于大规模互联网环境中。

6 结束语

本文通过分析传统的推荐系统的算法，在协同过滤算法的基础上，结合大规模网络的特性，提出一种基于网络分割与分组的协同过滤算法SCSG。该算法通过四种规则对网络进行分割、分组后，再利用协同过滤算法计算相似度，并进一步计算出预测评分，最终得到推荐项。该算法利用分治的思想，改善了传统算法在大规模应用场景中效率偏低的不足。算法主要探讨了如何对网络进行分割处理，网络中的其他细节，如合理构造常规项、制定项目分类标准等都有助于分割算法的进一步优化。

[1]Adomavicius G，Tuzhilin A.Toward the next generation of recommender systems：A survey of the state-of-the-art and possible extensions[J].IEEE Transactions on Knowledge and Data Engineering，2005，17（6）：734-749.

[2]Xu Hai-ling，Wu Xiao，Li Xiao-dong，et al.Comparison study of Internet recommendation system[J].Journal of Software，2009，2.（2）：350-362.（in Chinese）

[3]Zhang G W，Li D Y，Li P，et al.A collaborative filtering recommendation algorithm based on cloud model[J].Journal of Software，2007，18（10）：2403-2411.（in Chinese）

[4]Häubl G，Trifts V.Consumer decision making in online shopping environments：The effects of interactive decision aids[J].Marketing Science，2000，19（1）：4-21.

[5]Meng Xiang-wu，Hu Xun，Wang Li-cai，et al.Mobile recommender systems and their applications[J].Journal of Software，2013，2.（1）：91-108.（in Chinese）

[6]Huang Z，Chen H，Zeng D.Applying associative retrieval techniques to alleviate the sparsity problem in collaborative filtering[J].ACM Transactions on Information Systems（TOIS），2004，2.（1）：116-142.

[7]Deng Ai-lin，Zhu Yang-yong，Shi Bo-le.A collaborative filtering recommendation algorithm based on item rating prediction[J].Journal of Software，2003，14（9）：1621-1628.（in Chinese）

[8]Zhao Liang，Hu Nai-jing，Zhang Shou-zhi.Algorithm design for personalization recommendation systems[J].Journal of Computer Research and Development，2002，39（8）：986-991.（in Chinese）

[9]Zhou Jun-feng，Tang Xian，Guo Jing-feng.An optimized collaborative filtering recommendation algorithm[J].Journal of Computer Research and Development，2004，41（10）：1842-1847.（in Chinese）

[10]Zhang Feng，Chang Hui-you.Employing BP nerual networks to alleviate the sparsity issue in collaborative filtering recommendation system[J].Journal of Computer Research and Development，2006，43（4）：667-672.（in Chinese）

[11]Sarwar B M，Karypis G，Konstan J A，et al.Application of dimensionality reduction in recommender system—a case study[C]∥Proc of ACM Web KDD Workshop，2000：1.

[12]Breese J S，Heckerman D，Kadie C.Empirical analysis of predictive algorithms for collaborative filtering[C]∥Proc of the 14th Conference on Uncertainty in Artificial Intelligence，1998：43-52.

[13]Zhang Bing-qi.A collaborative filtering recommend action algorithm based on domain knowledge[J].Computer Engineering，2005，31（21）：7-9.（in Chinese）

附中文参考文献：

[2]许海玲，吴潇，李晓东，等.互联网推荐系统比较研究[J].软件学报，2009，2.（2）：350-362.

[3]张光卫，李德毅，李鹏，等.基于云模型的协同过滤推荐算法[J].软件学报，2007，18（10）：2403-2411.

[5]孟祥武，胡勋，王立才，等.移动推荐系统及其应用[J／OL].软件学报，2013，2.（1）：91-108.

[7]邓爱林，朱扬勇，施伯乐.基于项目评分预测的协同过滤推荐算法[J].软件学报，2003，14（9）：1621-1628.

[8]赵亮，胡乃静，张守志.个性化推荐算法设计[J].计算机研究与发展，2002，39（8）：986-991.

[9]周军锋，汤显，郭景峰.一种优化的协同过滤推荐算法[J].计算机研究与发展，2004，41（10）：1842-1847.

[10]张锋，常会友.使用BP神经网络缓解协同过滤推荐算法的稀疏性问题[J].计算机研究与发展，2006，43（4）：667-672.

[13]张丙奇.基于领域知识的个性化推荐算法研究[J].计算机工程，2005，31（21）：7-9.