基于灰色GA-LM-BP模型的CODMn预测

崔雪梅

(湖北工程学院生命科学技术学院,湖北孝感 432000)

(收稿日期:20120910 编辑:周红梅)

基于灰色GA-LM-BP模型的CODMn预测

崔雪梅

(湖北工程学院生命科学技术学院,湖北孝感 432000)

针对灰色GM(1,1)模型拟合误差较大和LM-BP神经网络泛化能力不强的问题,提出了灰色GA-LM-BP模型,该模型采用灰色GM(1,1)模型预测数据并得到其残差,利用LM-BP神经网络对残差进行拟合、测试、预测后,对灰色GM(1,1)模型的数据预测值进行修正从而得到较合理的预测值,并运用遗传算法对LM-BP神经网络的初始权值和阈值进行优化。运用该模型对伦河孝感段的CODMn进行了预测,预测误差不超过2.33％,表明模型的预测数据是合理的,可用于CODMn的预测和水质预警预报。

灰色理论;GA-LM-BP模型;化学需氧量;水质预测

化学需氧量(CODMn)是反映水中有机污染程度的指标,也是唯一能比较全面反映水中有机污染程度的指标,根据CODMn可以比较准确地计算废水有机污染物的排放总量[1-2]。用于预测CODMn的方法主要有逐步回归法、神经网络法、灰色预测法等[3-5]。利用微分方程描述灰色系统动态情况的模型,能反映地表水中CODMn浓度随时间变化的规律,但胡惠彬等[3]采用灰色GM(1,1)模型进行数据预测时,拟合误差比较大。LM-BP神经网络存在拟合能力强、泛化能力差的特点,采用多次拟合测试能够在一定程度上提高其泛化能力,但该方法需要反复试验,有时试验上万次还不一定能够取得很好的效果[6]。采用遗传算法对LM-BP神经网络的初始权值和阈值进行优化,能够提高其泛化能力[7]。

本文首先采用灰色GM(1,1)模型预测CODMn并得到其残差,再用LM-BP神经网络对该残差进行拟合,同时用遗传算法对LM-BP神经网络的初始权值和阈值进行优化。利用灰色LM-BP模型对残差进行拟合、测试、预测后,对灰色GM(1,1)模型的数据预测值进行修正,最后得到较合理的CODMn预测值。

1 灰色GA-LM-BP模型

1.1 灰色GM(1,1)模型

单序列一阶线性灰色GM(1,1)模型以微分拟合为核心,根据原始数据序列的特征,找出各数据之间的变化规律,它是灰色系统理论的基本预测模型,其动态预测建模过程[8-10]如下:

步骤1数据预处理。设系统原始数据为X0= {x0,1,x0,2,…,x0,k},进行一阶累加,生成的序列为

式中:k为原始序列数据的个数。

式中:a为发展系数;b为灰色作用量;z1,p为x1,p的紧邻均值生成序列。

GM(1,1)模型的白化微分方程[11]为

1.2 遗传算法

遗传算法是借鉴达尔文进化思想和遗传学理论演化出的一种随机搜索算法[12],其基本思想是:随机产生若干个所求解问题的数字编码,形成初始群体;通过适应度函数对每个个体进行评价,淘汰适应度低的个体,选择适应度高的个体参加遗传操作,生成下一代新的种群,再对这个新种群进行下一轮进化。

1.3 LM-BP神经网络

标准BP神经网络的基本思想是:将输出误差以一定的方式通过隐含层向输入层逐层反向传播,并传给各层的所有节点,最后根据各层节点的误差来修正各节点的权值。该方法速度慢,容易陷入局部极小值,针对该问题,人们提出了很多改进算法,其中LM(levenberg marquardt)算法是精度很高且速度最快的一种[6]。LM算法又称阻尼最小二乘法,它解决了标准BP神经网络的局部极小值问题。

LM算法对标准3层BP神经网络改进的主要步骤如下[13]:

步骤1初始权阈值初始化:随机产生初始权值和阈值,确定所有样本的误差平方和以及要达到的收敛准则ε,在编程中ε一般取1个很小的数。

中国家用电器研究院评测中心主任工程师梁晶以“用户体验及用户体验评测”为主题，从用户角度分享了冰箱技术升级的侧重点。她表示，从产品策划的角度来说，用户体验分为“有用”、“可用”、“易用”三个等级，三者都满足就能成为消费者青睐的好产品。未来冰箱企业创新，符合并挖掘用户需求是关键。

步骤2计算输出误差:对于r个输入层节点、n个隐含层节点、m个输出层节点的3层网络来说,隐含层第i节点输出ai为

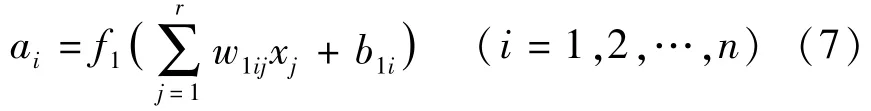
式中:w1ij、b1i分别为第1层(输入层)节点的权重和阈值;xj为隐含层的节点输入;f1为变换函数。

隐含层的节点输出为输出层的节点输入,输出层第j节点输出yj为

式中:w2ij、b2i分别为第2层即隐含层节点的权重和阈值;f2为变换函数。

输出层节点输出误差E为

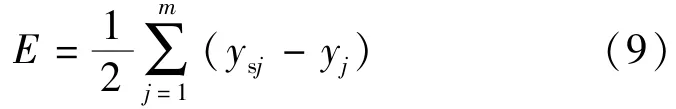
式中:ysj为期望输出。

步骤3计算雅可比矩阵:

式中:Su为第u层节点数;Q为训练样本数。

步骤4求BP网络权值的调整量Δwv:

式中:wv、wv+1分别为v、v+1时刻的权值;I为单位矩阵;μv为LM算法内部使用的一个大于零的调整因子,用于控制LM算法的迭代。通过自适应调整该值,LM算法可以完成梯度下降法与高斯牛顿法的较好结合。

1.4 灰色GA-LM-BP模型

灰色GA-LM-BP模型数据预测修正流程如图1所示。该模型的总体思想是:首先建立灰色GM(1,1)模型并预测数据,得到其残差。由于灰色GM(1,1)模型拟合精度不高,采用LM-BP神经网络对该残差进行拟合、测试、预测,同时采用遗传算法对LM-BP神经网络的初始权阈值进行优化。最后,将LM-BP神经网络得到的残差预测结果对GM(1,1)模型的数据预测值进行修正,得到合理的数据预测值。该模型包含灰色GM(1,1)预测和LM-BP神经网络的预测,其中LM-BP神经网络预测过程相对比较复杂,里面包含GA对LP-BP神经网络初始权阈值的优化。

遗传算法对LM-BP神经网络的初始权值和阈值进行优化的核心思想如下:①建立BP神经网络,设置好网络训练参数,随机初始化遗传算法GA种群;②将遗传算法种群的每组个体作为BP神经网络的初始权值和阈值,采用LM算法对BP神经网络进行训练;③将训练好的LM-BP神经网络对残差进行测试、预测,计算其均方误差,将均方误差作为遗传算法的评价函数,计算每个个体的适应度;④根据适应度对个体进行遗传(选择、交叉、变异)操作;⑤满足遗传代数g大于设定值的条件就结束,否则转第②步,进入下一代遗传。

在编程的过程中,可以求出所有代所有个体中适应度最小的值,并且记下此时神经网络的权值和阈值,这样就能保证网络经过多次训练多代遗传后,最终得到最优的网络参数。经过遗传算法对初始权值和阈值的优化后,神经网络的泛化能力将大幅增强。遗传算法适应度跟种群的个体之间是一种间接的关系,中间经过了神经网络的训练和测试,这是该模型实现的一个难点。

图1 灰色GA-LM-BP模型数据预测修正流程

2 实例应用

采用灰色GA-LM-BP模型对伦河孝感段的CODMn进行拟合、测试、预测。数据取样每2个月1次,采用2008年8月至2011年12月共21个月的CODMn监测数据。建立灰色GM(1,1)模型,得到CODMn的模拟值、残差及残差相对误差,如表1所示。

表1 灰色GM(1,1)模型对CODMn的拟合结果

由表1可见,灰色GM(1,1)模型的拟合精度不高,且残差的相对误差没有规律性,需采用灰色GALM-BP模型对数据进行修正。建立LM-BP神经网络,将最后3个数据作为测试数据,前17个数据作为拟合数据,BP网络输入层节点数为8,输出层节点数为1,经反复试验确定隐含层节点数为6比较合适。设置遗传算法个体(31个数据)变量的二进制位数为20,代沟为0.9,遗传代数为10。将遗传算法的种群个体作为LM-BP神经网络的初始权值和阈值,经过LM-BP神经网络训练后,对测试样本进行对比,求出其均方误差,将均方误差作为遗传算法的评价函数,进一步求出种群个体的适应度。经过10代遗传后,得到各代种群适应度的最优解和均值变化如图2所示。

图2 各代种群的最优解和均值的变化

利用灰色GA-LM-BP模型对灰色GM(1,1)预测得到的残差相对误差进行拟合,其拟合相对误差分别为:1.70×10-6、-2.87×10-7、6.68×10-8、-6.50× 10-6、-5.88×10-6、-2.90×10-6、-7.44×10-6、4.16× 10-5、1.96×10-6,可以看出灰色GA-LM-BP模型对训练样本基本上能百分之百拟合。对表1中最后3个残差数据的相对误差进行预测,预测的相对误差分别为-1.3831％、-0.32296％、-2.3206％,从预测结果可以看出,其误差均不超过2.33％,说明可以用该灰色GA-LM-BP模型对残差的相对误差进行预测。

最后,利用灰色GM(1,1)模型预测2012年2—10月的5个CODMn质量浓度数据,采用灰色GALM-BP模型对残差的相对误差进行预测,然后修正预测的CODMn质量浓度数据,最后得到较合理的CODMn质量浓度值,如表2所示。

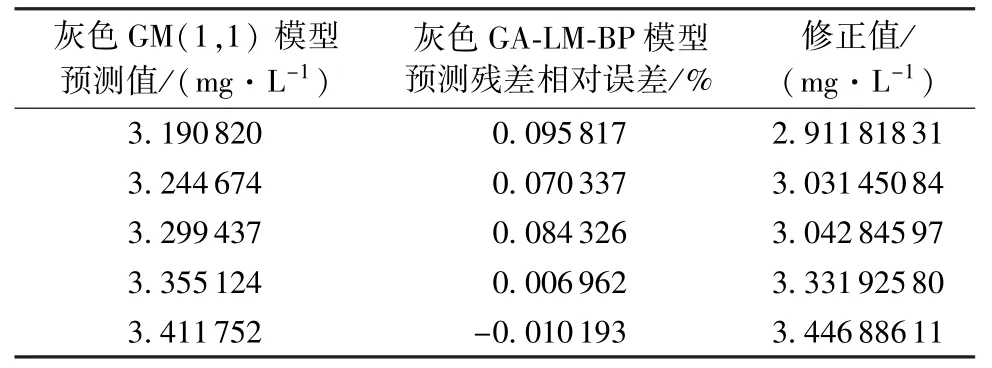
表2 CODMn质量浓度灰色预测、修正结果

3 结 语

灰色GA-LM-BP模型是一种有效的水质预测方法,其吸收了灰色预测方法、遗传算法和LM-BP神经网络的优点,但同时也增加了编程的复杂性和计算工作量,主要体现在遗传算法的优化过程中。运用灰色GA-LM-BP模型对伦河孝感段21个月的CODMn实测数据进行拟合、预测,应用结果表明,采用该模型对本地区的CODMn值进行预测是合理可行的,一方面该方法利用灰色GM(1,1)模型能很好地反映本地区河流CODMn值随时间的变化规律,另一方面可以采用LM-BP神经网络的残差预测结果对预测数据进行修正,得到合理的预测数据。

[1]朱玉磊.化学需氧量几种测定方法研究[J].科技资讯, 2008,28(10):83-85.(ZHU Yulei.The research of determination of chemical oxygen demand(COD)[J]. Science＆Technology Information,2008,28(10):83.(in Chinese))

[2]远振海,鲁治冰.基于神经网络的COD值预测研究[J].黑龙江水专学报,2008,35(1):84-86.(YUAN Zhenhai,LU Zhibing.COD data forecast based on NN[J]. Journal of Heilongjiang Hydraulic Engineering College, 2008,35(1):84-86.(in Chinese))

[3]胡惠彬.灰色系统的GM(1,1)模型在地表水COD浓度预测中的应用[J].中国环境监,1993,9(4):45-46. (HU Huibin.Application of grey system GM(1,1) models in forecasting cod concentration of surface water [J].Environmental Monitoring in China,1993,9(4):45-46.(in Chinese))

[4]刘玉存,于国强,王少华,等.基于神经网络的传爆药废水COD去除率预测研究[J].含能材料,2009,17(3): 361-364.(LIU Yucun,YU Guoqiang,WANG Shaohua,et al.Elman model in prediction of COD removal rate of booster explosive wastewater[J].Chinese Journal of EnergeticMaterials,2009,17(3):361-364.(in Chinese))

[5]赵英,崔福义,郭亮,等.基于BP神经网络的天津于桥水库CODMn预测研究[J].南京理工大学学报:自然科学版,2008,32(3):376-380.(ZHAO Ying,CUI Fuyi, GUO Liang,et al.CODMnforecast based on BP neural network at Yuqiao Reservoir in Tianjin[J].Journal of Nanjing University of Science and Technology:Nature Science,2008,32(3):376-380.(in Chinese))

[6]阮仕平,党志良,胡晓寒,等.基于LM-BP算法的综合水质评价研究[J].水资源研究,2004,25(1):12-14. (YUAN Shiping,DANG Zhiliang,HU Xiaohan,et al. Study on comprehensive water quality assessment based on LM-BP algorithm[J].JournalofWaterResources Research,2004,25(1):12-14.(in Chinese))

[7]GUOhairu,LIZhimin.Amethodofimproving generalization ability for neural network based on genetic algorithm[C]//2010 IEEE International Conference on Intelligent ComputingandIntelligentSystems(ICIS 2010).Beijing:IEEE PRESS,2010:742-745.

[8]刘思峰,谢乃明.灰色系统理论及其应用[M].第4版.北京:科学出版社,2008.

[9]邓聚龙.灰色系统基本方法[M].武汉:华中科技大学出版社,2004.

[10]周媛,朱大奇.水下机器人传感器故障诊断的灰色预测模型[J].中国造船,2011,52(1):137-144.(ZHOU Yuan,ZHU Daqi.A sensor fault diagnosis method for underwater vehicles based on GM(1,1)[J].Shipbuilding of China,2011,52(1):137-144.(in Chinese))

[11]阎威武,常俊林,邵惠鹤.基于滚动时间窗的最小二乘支持向量机回归估计方法及仿真[J].上海交通大学学报,2004,38(4):524-527.(YAN Weiwu,CHANG Junlin,SHAO Huihe.Least square SVM regression method based on sliding time window and its simulation[J]. Journal of Shanghai Jiaotong University,2004,38(4): 524-527.(in Chinese))

[12]原思聪,江祥奎.基于GA-BP神经网络的双目摄像机标定[J].西安建筑科技大学学报:自然科学版,2011, 43(4):604-608.(YUAN Sicong,JIANG Xiangkui. Binocular camera calibration based on GA-BP neural network[J].Journal of Xi'an University of Architecture＆ Technology:Natural Science Edition,2011,43(4):604-608.(in Chinese))

[13]缪新颖,褚金奎,杜小文.LM-BP神经网络在大坝变形预测中的应用[J].计算机工程与应用,2011,47(1): 220-222.(MIAO Xinying,CHU Jinkui,DU Xiaowen. Application of LM-BP neural network in predicting dam deformation[J].Computer Engineering and Applications, 2011,47(1):220-222.(in Chinese))

Prediction of CODMnvalue based on the grey GA-LM-BP model

//CUI Xuemei(College of Life Science and Technology,Hubei Engineering University,Xiaogan432000,China)

Due to the large fitting-errors of grey GM(1,1)model and the weak generalization ability of LM-BP neural network,a model of grey GA-LM-BP network was proposed in this paper.The grey GM(1,1)model was used to predict data and obtain residual errors.After the residual errors were fitted,tested and forecasted with LM-BP neural network, more reasonable predicted values can be obtained by correcting the predicted values of the GM(1,1)model.In the meantime,the initialized weights and threshold of LM-BP neural network were optimized with the genetic algorithm(GA). The grey GA-LM-BP model was then used to predict the CODMnvalues at the Xiaogan segment of Lunhe River.Since the prediction errors were found to be less than 2.33％,the accuracy of the model is considered to be reasonable.The model can be used to predict the CODMnvalues and the water quality early warning.

grey theory;GA-LM-BP model;CODMn;water quality prediction

(收稿日期:20120910 编辑:周红梅)

10.3880/j.issn.10067647.2013.05.009

TP181;X703.1

A

10067647(2013)05003804

湖北省教育科学“十一五”规划课题(2009B106);湖北工程学院项目(Z2011019)

崔雪梅(1979—),女,云南宣威人,讲师,硕士,主要从事生态环境及智能预测研究。xgughr@126.com