多工况下SF33900自卸车A型架拓扑优化设计

吕 斌， 唐华平， 谭永青， 李 平， 黄小青

（中南大学 机电工程学院，湖南 长沙 410083）

大型自卸车是一种主要用于大型露天煤矿和大型土木工程的工程机械，随着我国经济的快速发展，大型自卸车的需求量正在稳步上升。人们对自卸车的要求也越来越高，对车辆各部分零件的使用寿命、稳定性及平顺性提出了更高的要求［1］。大型自卸车结构庞大，因矿山工作环境复杂、行驶路况恶劣及载重量大，矿用自卸车结构件容易产生破坏失效。而减小自卸车各结构件最大应力值，并使结构件应力分布均匀，是提高自卸车寿命的重要保证。目前，国内外对大型矿用自卸车结构性能分析和结构优化进行了大量研究［2－6］，但是对于自卸车结构件拓扑优化设计的研究还较少，在优化设计中只是改良局部高应力区域，并不能得到一个应力分布均匀的最优化全新结构。

本文针对SF33900自卸车在国内某矿山使用时出现A型架焊缝开裂现象，对A型架局部应力过大的现象进行强度分析与结构优化，使其在多种复杂工况下满足使用强度和制造可行性要求。

1 自卸车A型架受力分析

大型自卸车是由车架、后桥壳、A型架、驾驶室、电器柜、油箱等很多部件组成，在分析前桥A型架的强度前，先要通过整车的动力学分析得出A型架受力情况。

如图1所示，先通过SolidWorks建立起三维自卸车模型，在各连接部件加上相应的约束关系就完成了动力学模型。如左、右举升油缸的上端部分和举升机构主体之间的运动副定义为旋转副；货物与车厢之间运动量相对很小，它们之间的运动副定义为固定副；车厢与纵梁之间的运动副定义为球铰副等。

自卸车模型悬架刚度和阻尼是非线性的，通过计算可以得到其变化曲线，然后通过Spline曲线导入到ADAMS中。

自卸车工作的路面十分恶劣，路况多样，将其分为7种工况进行模拟分析。

工况1 启动—加速到最高速。模拟卡车满负载下承受1g垂直载荷和向前0.3g加速度。

工况2 30km／h紧急制动。模拟卡车满负载下承受1g垂直载荷和0.3g刹车减速。

工况3 下坡转弯行驶。模拟卡车满负载下16%的坡和承受0.3g转弯的横向加速度。

工况4 下坡转弯制动。模拟卡车满负载下爬16%的坡 、承受0.3g转弯的横向加速度和0.3g刹车减速，此为最恶劣工况。

工况5 上坡行驶。模拟卡车满负载爬16%的坡。

工况6 上坡转弯行驶。模拟卡车满负载爬16%的坡 和承受0.3g转弯的横向加速度。

工况7 凸凹路面行驶。模拟卡车满负载下经过一条沟，其中一个前轮脱离地面。

图1 整车三维模型

通过ADAMS仿真7种工况，得出SF33900自卸车A型架受力情况，见表1所列。当发生转弯工况时，对转向横拉杆的2个支座处分别施加360 000N压力和274 500N的拉力。

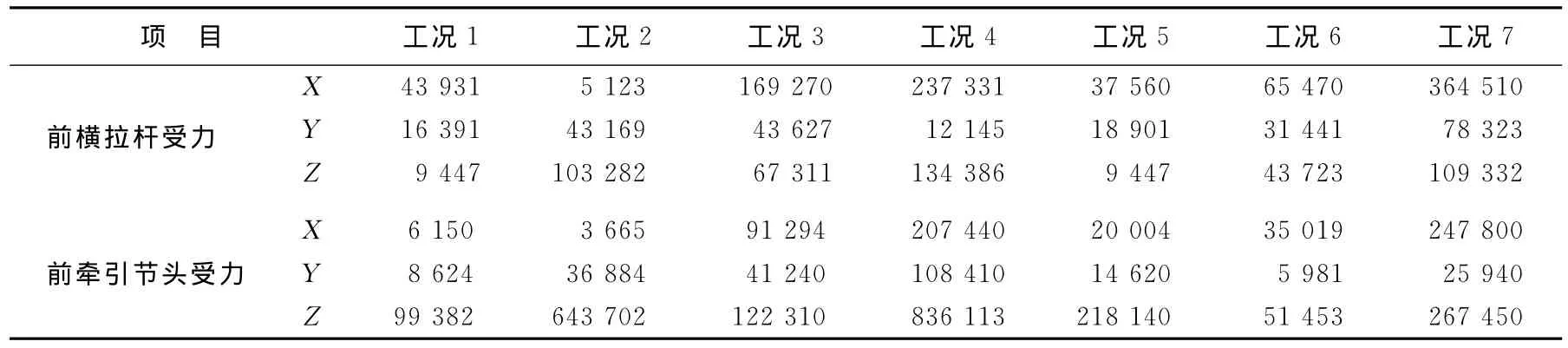
表1 7种工况下A型架在X、Y、Z向受力情况 N

2 静力学分析和试验测试

（1）各种工况有限元分析。有限元模型原则上应尽量按照实际物体的几何结构建立，但对于结构复杂又对结果影响不大的局部位置可以进行适当简化，建模时可以去掉一些不必要的细节和间隙，如倒角、螺栓及螺栓孔等。在SolidWorks中建立三维模型，其中销轴、前横拉杆和前牵引节头用体模型，其他部分建立面模型。导入Hypermesh中，用3D单元划分体模型，用2D单元划分面模型。分别赋予各单元的材料，A型架重要部位选用SUMITEN 610E材料，其弹性模量为206GPa，泊松比为0.3，密度为7 850kg／m3，屈服强度为480MPa。对销轴进行全约束，然后根据表1中的工况4加力，在Hypermesh中建立有限元模型，如图2所示。在RADIOSS求解器中进行求解和Hyperview模块中进行后处理，得出应力云图，如图3所示。

（2）试验测试。试验测试时，让自卸车在7种工况下工作，在A型架上选取9个主要点进行应力测量，测试点位置如图4所示，各测点均布贴45°应变花。

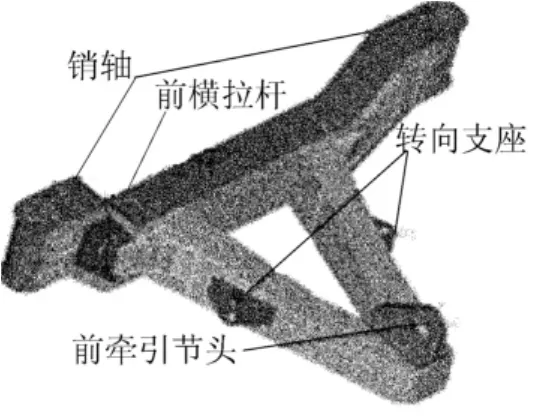
图2 有限元模型

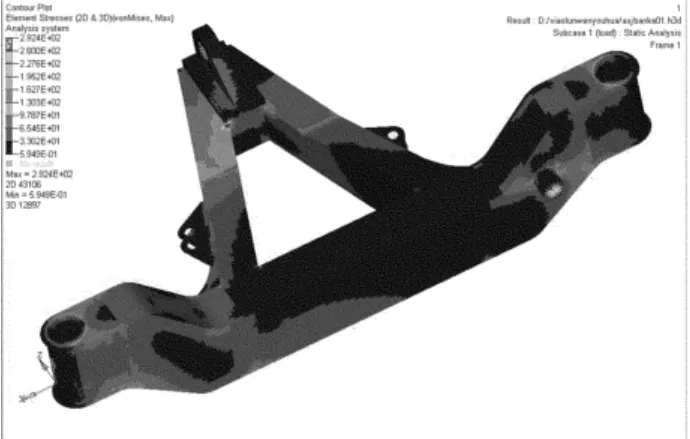
图3 老A型架应力云图

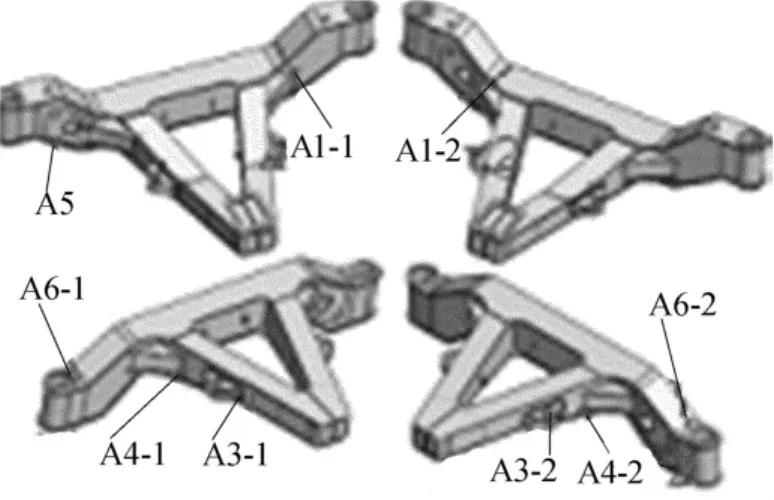
图4 A型架测试点位置

测试信号主应力大小按（1）式进行合成：

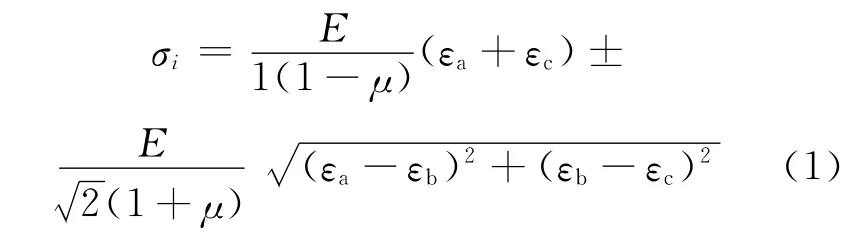
其中，杨氏模量E为2.07×105MPa；泊松比μ为0.27。在最恶劣工况下的坡制动转弯工况下，其工作应力见表2所列。

由表2中可知，试验与仿真的误差控制在10%左右，因此仿真结果是可信的。但可以明显看出各部分受力分布极其不均匀，因而对A型架进行拓扑优化，改善其受力分布很有必要。

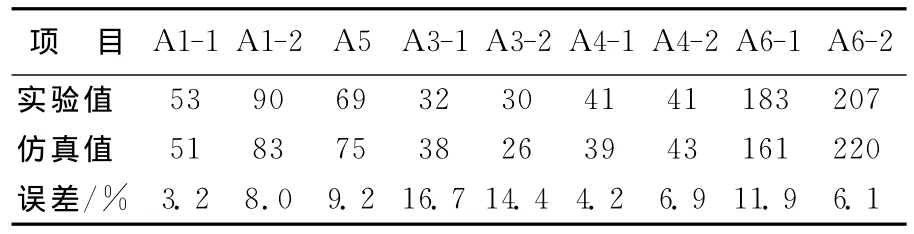
表2 实验与仿真应力比较 MPa

3 自卸车A架结构拓扑优化

3.1 结构拓扑优化理论基础

结构优化主要分为拓扑、形貌及尺寸优化，而拓扑优化是一种比尺寸优化、形状优化更高层次的优化方法，也是结构优化中最为复杂的一类问题［7－11］。拓扑优化处于结构的概念设计阶段，其优化结果是一切后续设计的基础，对A型架主要进行拓扑优化。

拓扑优化方法主要有均匀化方法、密度法、变厚度法和拓扑函数描述方法等，其中变密度法是连续体拓扑优化的常用方法。变密度法中，常用的插值模型主要有固体各向同性惩罚微结构模型（Solid Isotropic Microstructure with Penalization，简称SIMP），其材料模型为：

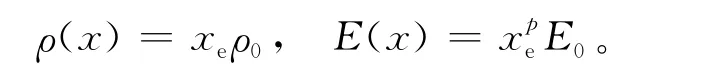
其中，xe为每个单元的相对密度；ρ（x）为拓扑优化设计变量；ρ0为设计区域每个单元的固有密度；E（x）为优化后的弹性模量；E0为初始弹性模量；p为惩罚因子。

在建立可靠的优化模型后，还需要选择收敛速度快且计算不是很复杂的优化算法，目前适用于拓扑优化的优化算法主要包括分析型求解方法和数值型求解方法2种类型。前者也称为优化准则法，后者又称为数学规划算法，本文中主要采用优化准则算法。采用HyperWorks中的OptiStruct模块对自卸车A型架结构进行拓扑优化设计，利用SIMP插值方法作为材料模型，用优化准则法作为优化算法，同时采用下限约束法和周长约束法控制数值不稳定现象。

本文中A型架拓扑优化以应力作为约束条件，以整体体积最小作为目标函数，在多工况作用下，基于变密度法拓扑优化数学模型为：

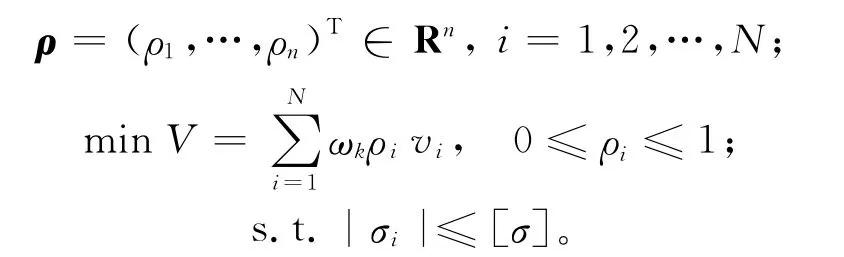
其中，ρ1，…，ρn为单元设计变量；vi为i单元的体积；σi为i单元的工作应力；［σ］为许用应力；N为单元总数；ωk为第k个工况的权值。

根据各种工况对自卸车的拓扑优化重要程度确 定 权 值，即ω1、ω2、ω3、ω4、ω5、ω6、ω7分 别 为15%、20%、10%、10%、10%、15%、20%。

3.2 A型架的拓扑优化

由A型架的应力分布值可知，A型架的最大应力为292.4MPa，且大部分材料应力较小，低于80MPa，应力分布不均匀，材料也存在大量的浪费。为了减轻支架质量，降低成本，对A型架进行拓扑优化设计，制定拓扑优化流程，如图5所示。

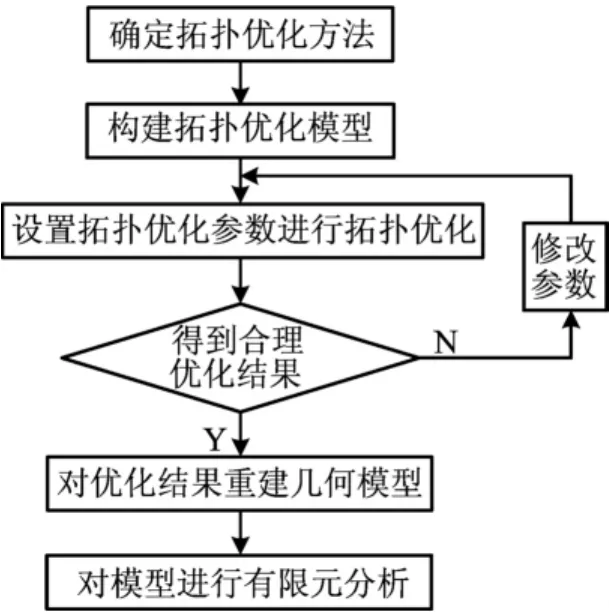
图5 拓扑优化流程图

根据A型架的安装位置和各个支撑点的受力要求，确定了销、转向支撑、前横拉杆、前牵引节头为非设计部件，而且它们的原本位置不变化，根据这些要求得到A型架拓扑优化模型，如图6所示。

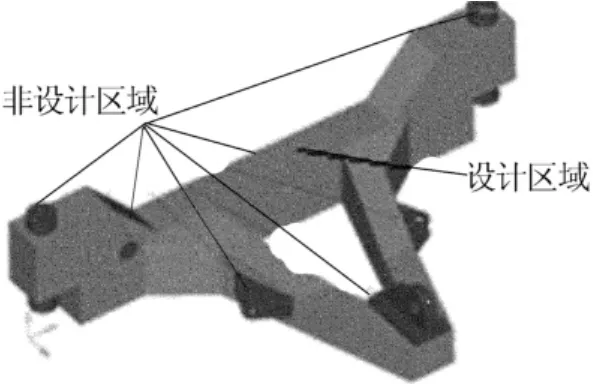
图6 A型架拓扑优化模型

非设计区域和设计区域都使用四面体单元，单元尺寸为20mm，单元个数为1 203 448个，对销轴进行全约束，然后根据7种工况，在 Hypermesh中建立拓扑优化有限元模型，大车在现场工作时，各个部件的应力值越小、质量越轻越好。根据这些要求，采用HyperWorks中的OptiStruct模块进行A型架的拓扑优化：目标为各种工况下加权体积最小，约束为A型架的应力值限制在150MPa，设计变量为单元密度。

在拓扑优化时，同时要考虑到制造工艺的约束，对于前桥，主要考虑A型架左、右两边的对称情况和棋盘格现象的消除。经过计算，得到图7所示的A型架拓扑优化结构。

从拓扑优化结果可以看出，A型架结构不再是封闭式结构，上、下盖板也有明显的变化，筋板的数量和位置也有一定的改变，将拓扑优化模型导入SolidWorks后，经过整理简化，得到图8所示的几何模型。

继续将几何模型导入到Hypermesh中，重新网格划分和计算，材料属性、力和约束的施加与前面情况一样，得到应力云图，如图9所示。

图7 A型架拓扑优化结构

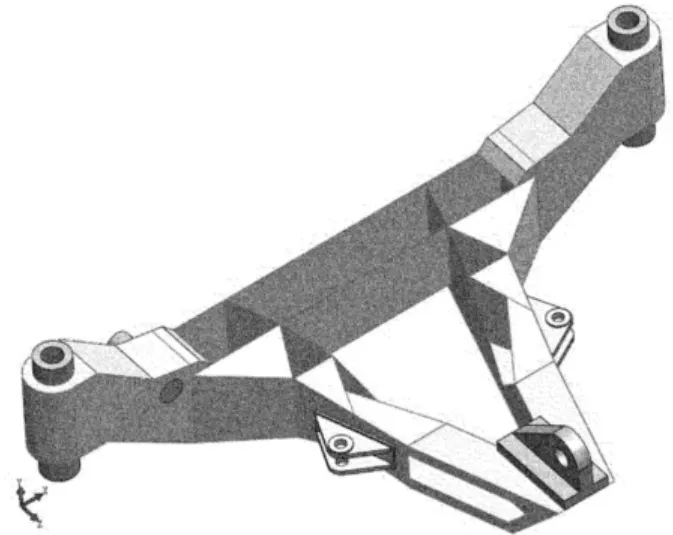
图8 新A型架几何模型

图9 新A型架应力云图

比较旧、新A型架情况，旧A型架质量为4 300kg，最大应力为292.4MPa；新A型架质量为4 000kg，最大应力为240.1MPa。可知经过拓扑优化后，A型架质量减少了6.9%，最大应力减少了17.8%，应力分布更加均匀化，与旧A型架的封闭式结构相比，优化结构在加工生产时可以采用双面角焊，增加了结构的疲劳寿命，拓扑优化的效果较好。同时对新A型架按表1中的其他6种工况进行分析，都能满足强度要求。

4 结论

（1）多体动力学分析为SF33900自卸车A型架的应力分析提供了7种工况的载荷条件，选择其中最恶劣工况进行应力分析，通过实验结果和仿真结果比较，可知有限元模型是有效的。

（2）通过给定不同工况的权值，将多工况目标转化成单目标对SF33900自卸车A型架进行拓扑优化，新A型架结构不再是封闭式结构，上、下盖板也有明显变化，筋板的数量和位置也有一定的改变。新的A型架结构比老结构质量减轻6.9%，最大应力减小17.8%，并且应力分布均匀，从而使拓扑优化结构更加适合于加工和制造。

［1］万海如，唐新蓬，段家典.重型矿用电动轮自卸车的现状和发展趋势［J］.重型汽车，2001（1）：24－26.

［2］邹 琳，于海昌，景俊鸿.6×4重型自卸车车架有限元分析［J］.合 肥 工 业 大 学 学 报：自 然 科 学 版，2007，30（Z1）：43－47.

［3］闰振华.矿用自卸车车架静态及动态应力数值模拟研究［D］.长春：吉林大学，2007.

［4］赵永辉.大客车车身骨架结构拓扑优化设计［D］.武汉：武汉理工大学，2008.

［5］展 新.卡车车架轻量化设计［D］.长春：吉林大学，2010.

［6］赵雪梅.铝合金半挂车关键结构拓扑优化轻量化设计［D］.长春：吉林大学，2011.

［7］左孔天.连续体结构优化设计理论与应用研究［D］.武汉：华中科技大学，2004.

［8］范文杰，范子杰，桂良进，等.多工况下客车车架结构多刚度拓扑优化设计研究［J］.汽车工程，2008，30（6）：531－533.

［9］Bends M P.Sigmund O.Topology optimization：theory，methods and applications ［M ］.Berlin： Springer，2003：53－69.

［10］于开平，周传月.Hypermesh从入门到精通［M］.北京：科学出版社，2005：83－120.

［11］张胜兰，郑冬黎，郝 琪，等.基于Hyperworks的结构优化设计技术［M］.北京：机械工业出版社，2007：159－183.