Detection of Bearing Fault Signal Based on the Wavelet and Chaos Theory
REN Xueping,LIU Tongtong
Mechanical Engineering School,Inner Mongolia University of Science & Technology,Baotou 014010,China
1.Introduction
Bearing is one of the most common parts in mechanical equipments and the running state directly affects the function of the equipment.Since the precision of modern mechanical equipment is getting higher and higher,any slight fault or disturbance may cause a great error to the product and it will bring huge economic losses.Detection of the fault bearing at the first time is an important way to improve the quality of products.Therefore,it is necessary to find an effective method to judge the failure of bearings.
During the practical application process of mechanical equipment,the characteristic signal of bearing failure is very weak at the beginning time of bearing failure due to the complexity of equipment which contains all kinds of spare parts and different spare parts have different vibration frequency and amplitude.Therefore,the signal of bearing failure is often submerged in other interfering signals and how to identify this weak signal from the background strong noise is very important for the signal processing and fault diagnosis[1].
2.The basic theory
2.1.wavelet packet de-noising
The signals collected at the workplace are also the mixture of other signals.It always contains some bandwidth of the signals.If the Duffing oscillator is directly adopted to process the original signal,it will not only waste a lot of processing time,but also will affect the accuracy.Therefore,it is necessary to denoise the original signals before these signals are analyzed.The conventional way to denoise the signals can only give us a given frequency of the signal which may not what we want.However,if the wavelet packet of de-noising is adopted,any band of signals could be obtained.Therefore,the wavelet packet of de-noising will become one of the main methods to reduce the noise signals in the future.
The wavelet packet of de-noising could be divided into the following four steps[2]:① The wavelet packet,② Calculate the champion tree and determine the optimal basis of wavelet packet,③Threshold the decomposition coefficients of wavelet packet,④ Reconstruction of wavelet packet.
From the above steps,it could be seen that how to choose the threshold and threshold quantization is the key part and it is directly related to the reduction quality of the noise signal.
If the noise signals will be reduced from a given analogue signal which is given as follows:
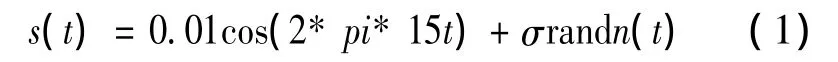
Where,randn(t)is the white noise whose mean is zero and it meets the normal distribution,σ is the standard deviation of noise and the value of σ is 1,the amplitude and frequency of the weak signal is 0.01 and 15,respectively.
As shown in Fig.1 is the waveform diagram before and after the wavelet packet de-noising.
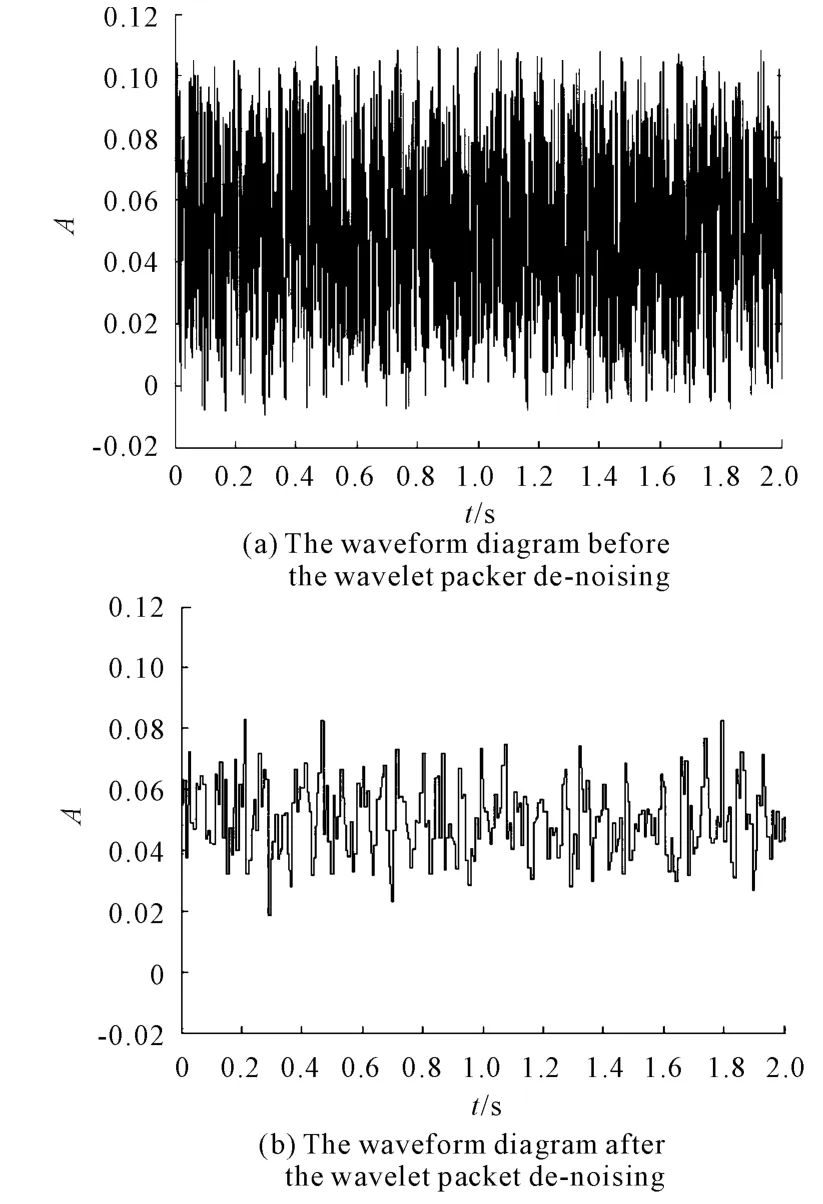
Fig.1 the waveform diagram before and after the wavelet packet de-noising
The variable ofs'(t)is used to present the signal after the de-noising process of wavelet packet.
2.2.The Duffing oscillator equation
For small amplitude periodic signal,it is close with the inner driving force angular frequency to disturbance the Duffing equation.If the influence of harmonic is considered,the result of Duffing oscillator equation could be written as follows[3-4]:
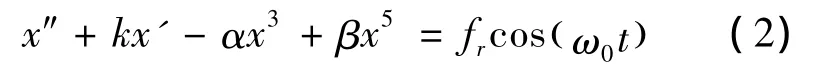
Where,frcos ω0( )tis Cycle policy dynamics,is Subsidence ratio,kis The angular frequency of the inner driving force,ω0is The nonlinear restoring force.-αx3+βx5Use the fourth order Runge Kutta method[5]to numerically solve the equation(2)and definex'=y,the formula(2)could become as follows:

Ifk=0.5 in the equation(3),calculate the maximum lyapunov index[6]of Duffing oscillator equation with the method of Wolf,the maximum lyapunov index is shown in Fig.2.From this figure,it is clearly shown that the Duffing oscillator equation of the critical threshold is fr=0.685.
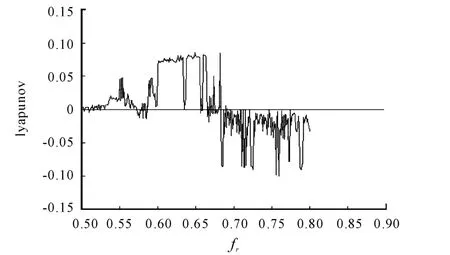
Fig.2 Analog signal maximum lyapunov index
The signals after wavelet packet de-noising were added to equation 3 and the following equation could be obtained.
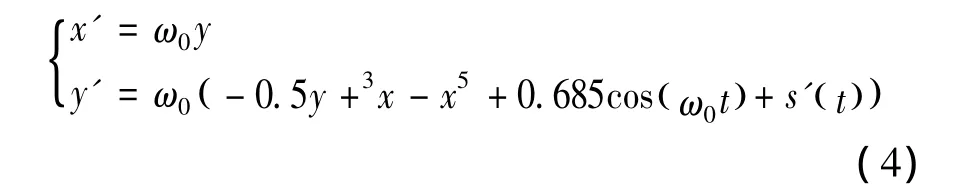
Where,s'(t)is the signal after the wavelet packet de-noising.The phase track diagram of Duffing equation before and after joining the signals are shown in Fig.3.
As shown in Fig.3,the system was changed from chaotic status to periodic status when the test signal was added.A weak periodic signal of 15 Hz was obtained according to the basic theory of Duffing equation and this coincides with the added signal.
3.Analysis of roller bearing fault
In this paper,the experiments were tested according to the bearing experimental data in electrical engineering and computer science of Western Reserve University to verify whether the practical problems could be solved by using the method of the wavelet packet de-noising and the chaos theory.It was ana-lyzed that the bearing outer ring faults of 6502 2RS SKF bearing could be detected when the rotation speed was 1750r/min.In this case,the faults was a tiny round pit with 0.007″made by EDM method,the roll diameter is 8 mm,pitch circle diameter is 40 mm,number is 9,roller contact angle is 0,the sampling frequency is 12 000 Hz,sampling point is 5 050,calculated engine speed is 1 750 r/min.The bearing components fault frequencies are shown in Tab.1.

Fig.3 The system phase track diagram

Tab.1 Frequency of each position fault of bearing
Firstly,the fault signal was denoised by the wavelet packet,and the obtained wave patterns are shown in figure 4.
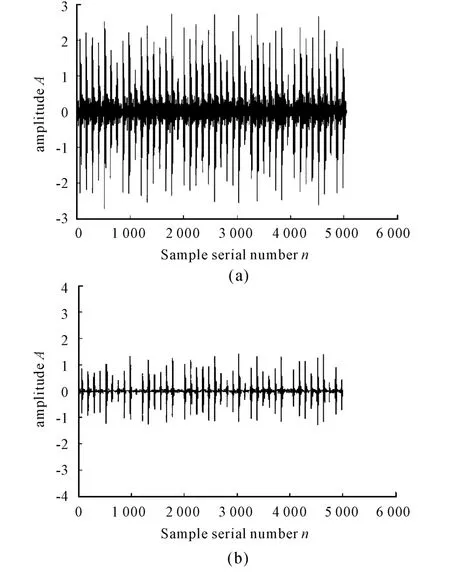
Fig.4 Before and after the wavelet packet de-noising the bearing outer ring fault signal waveform
As shown in Fig.5,the power spectrum are preliminarily analyzed by the wavelet packet.The obtained failure frequency of signal mainly appears between 80 Hz and 150 Hz as shown the power spectrum in Figure 5(b).
According to the various characteristics parameter of bearing outer ring,the Duffing oscillator equation could be designed as shown in equation 5.
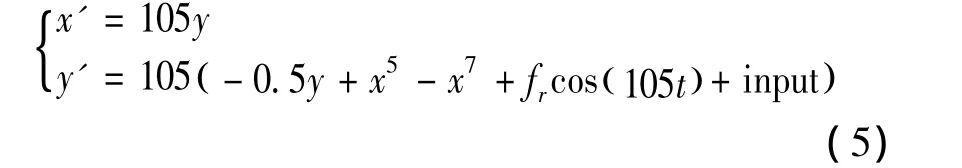
To evaluate the maximum lyapunov index of Duffing oscillator equation,the maximum lyapunov index is shown in Fig.6.From this figure,it could be seen that the Duffing oscillator equation of the critical threshold,i.e.fr,is 0.737.

Fig.5 the signal power spectrum diagram with wavelet packet transform

Fig.6 The maximum lyapunov index of the bearing outer ring
In order to further analyze the bearing fault signal after wavelet packet de-noising by using Duffing oscillator equation,the phase track diagram were presented in Figure 7.
From Fig.7,it could be seen that the phase trajectory of system mutations only when the fault signal of bearing outer ring is added.If other signals are added,the phase trajectory of system could be also in chaos states.Consequently,a conclusion could be drawn that the system is only sensitive to some specific frequency of fault signal and then the location of the fault could be determined.Therefore,these results confirmed that the proposed method in this paper could be used to diagnose the rolling bearing fault.

Fig.7 The phase track diagram of Duffing oscillator equation
4.Conclusions
In this paper,the combination of wavelet packet de-noising and chaos theory was adopted to distinguish the fault signal of bearing outer ring.The basic theory and feasibility have been comprehensively analyzed.
Through the real application of experimental data,it has been confirmed that the proposed method has high accuracy and it is capable to distinguish large SNR of bearing fault signal.Furthermore,this method is comparatively simple and effective and it could be applied to detect the fault of the bearing in the future.
[1]GUO Yuxiu,NI Xiaohong,WANG Yutian.Study on the fault diagnosis of rolling mills based on the chaos weak signal detection method[J].Journal of Engineering Design,2011,18(3):218-221.
[2]LI Dengfeng,YANG Xiaohui.Wavelet theory and application examples[M].Bei Jing:Advanced Education Press,2010.
[3]LI Xianglian.Detection by Chaotic Oscillator on Weak Signal Slowly Frequency Change of Mechanical Vibration[J].Chinese Journal of Mechanical Engineering,2006,17(1):12-16.
[4]WANG Lixia.Weak Signal Detection Based on Chaos Theory[D]. Harbin :Harbin Engineering University,2011.
[5]ZHU Yeming,QIAO Zongmin.The Solution to a Mathematical Modeling Problem Based on Matlab[J].Journal of Anqing Teachers College:Natural Science Edition,2006,12(1):42-45.
[6]HAFSTEIN S F.A constructive converse Lyapunov theorems on asymptotic stability for nonlinear autonomous ordinary differential equations[J].DynamicalSystems,2005,20(3):281-299.
[7]REN Xueping,MA Wensheng.Speed Reduce Fault Diagnosis Base on Wavelet and Envelope Analysis[J].Coal Mine Machinery,2008,29(2):205-206.
[8]Case Western Reserve University Bearing Data Center Website[EB/OL].[2013-02-19].http://www.eecs.case.edu/laboratory/bearing/.
- 机床与液压的其它文章
- Strength Analysis and Optimization of a Torsion Beam Rear Suspension
- Development of Vibration Signal Acquisition and Analysis System for Machine Tools Based on LabVIEW
- Numerical Analysis and Experimental Research on Micro Milling Process with Cycloidal Tool Path
- Analysis of the Optimization of Gear Pump Pulsation Based on Matlab
- Simulation Evaluation and Performance Analysis of a Double Coil Magnetorheological Valve
- Remote Condition-based Maintenance Approach to Hydraulic System of Construction Machinery

