基于有限元法的细长薄壁件车削过程的振动分析

冯 利，牛海侠

（正德职业技术学院，江苏南京 211106）

现代加工技术特别是从数控技术引进到加工领域后有了飞跃式发展，对细长薄壁件的加工精度也越来越高。无论从机械加工还是被加工件在加工过程中的动态特性对产品的影响越来越受到重视。

细长薄壁件的加工一直被制造行业认定为加工难题，长径比一般都大于10，车削时加工工艺系统的刚性较差，及细长薄壁件热扩散性差，工件极易弯曲且产生振动，使工件容易产生腰鼓形、扭曲等缺陷，不易获得满意的表面粗糙度及几何精度。

1 计算模型

细长薄壁件的几何特点和车削加工方法决定其在加工过程必须考虑其动态性能，本文利用有限元软件针对细长薄壁件固有振动特性进行分析，得出某细长薄壁件的固有频率和振型，对进一步分析、控制加工误差有非常重要的意义。

装夹方式及力学模型如图1和图2所示。

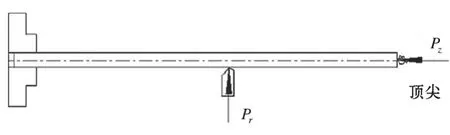
图1 细长薄壁件切削受力图

图2 某细长薄壁件结构示意图

模态分析。

本文选用实例：一细长薄壁件的材料为40Cr调质，长600 mm，外径50 mm，内径44 mm，车削速度为800 r/min。选用20节点的二次单元对结构进行网格画分，并全部分成计算精度较高的六面体网格，共得到325 671个网格单元。

对三角卡盘卡紧的位置作位移全固定约束，对另一端顶尖顶到的位置作径向约束，由于刀具切削点也有切向力作用于切削点，且随着加工的进行切削点在变化，本文对切削点在不同位置时分别作模态计算，以期得到其振动规律[1-2]。

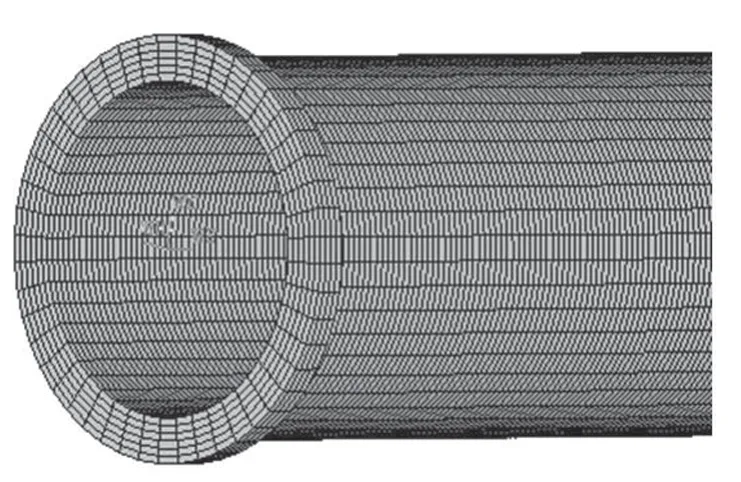
图3 某细长薄壁件结构示意图

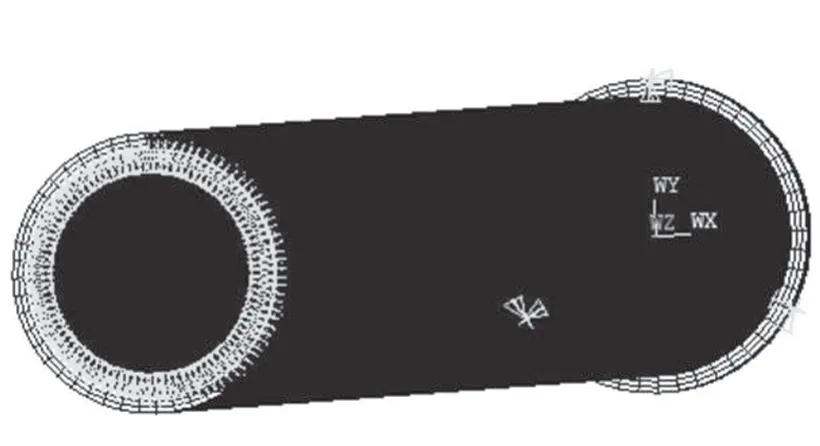
图4 某细长薄壁件结构示意图

2 有限元分析（FEA）

有限单元法是利用计算机进行的一种数值分析法。它在工程技术领域中的应用十分广泛，几乎所有的弹塑性结构静力学和动力学问题都可用它求得满意的结果。

分析过程中包含以下三个步骤。

步骤一：创建有限元模型。包括：（1）创建或读入有限元模型；（2）定义材料属性；（3）划分网格（节点及单元）。

步骤二：施加载荷并求解。施加载荷及载荷选项、设定约束条件，然后求解。

步骤三：查看结果。查看分析结果，然后检验结果（分析是否正确）。

3 计算结果

计算结果如表1所示。

刀离顶尖0%时前四阶模态对应的振型如表2所示。

可见，一阶和二阶都为一节点弯曲振动，三阶为扭转振动，四阶为二节点率曲振动。

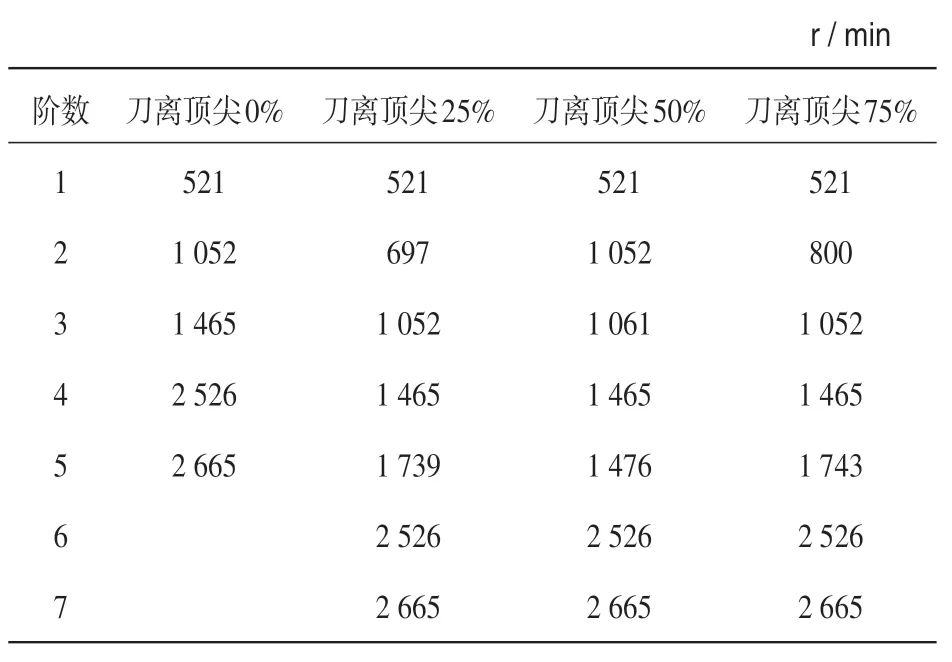
表1 车刀离顶尖距离（占总长的百分比）不同时对应的转速

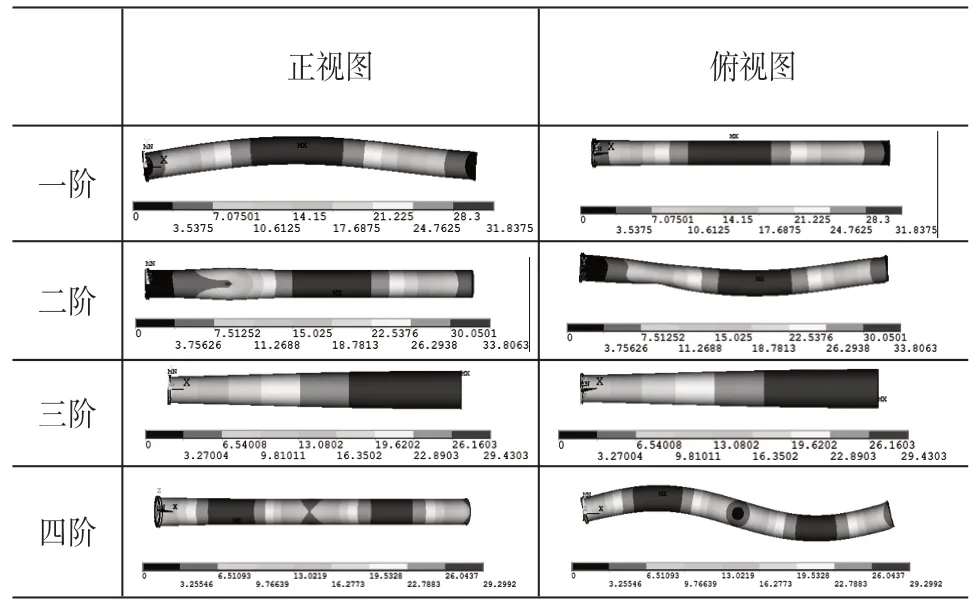
表2 振型图

4 结论

（1）在车削开始时，加工过程并无共振现象发生，可以保证加工精度；

（2）车削过程中，当车刀到达离顶尖端为工件总长的75%时，工件的二阶模态频率与车削转速相同，车削转速即其激振源，达到共振后使振动幅度增大，加工精度突然下降；

（3）建议对此工件再加工时使用跟刀架，以改变支承状态，使第二阶模态频率有所升高，避开车削转速造成的共振频率，以保证不发生共振，提高加工精度。

［1］韩荣第，郭建亮.细长杆车削浅析［J］.机械研究与应用，2004（1）：11-15.

［2］杨红义，李卫民.基于ANSYS的细长轴车削过程中的模态分析［J］.辽宁工业大学学报：自然科学版，2008（4）：242-245.