Progress in numerical simulation of cavitating water jets*

PENG Guoyi, SHIMIZU Seiji

College of Engineering, Nihon University, Koriyama, Fukushima 963-8642, Japan, E-mail: peng@mech.ce.nihon-u.ac.jp

Progress in numerical simulation of cavitating water jets*

PENG Guoyi, SHIMIZU Seiji

College of Engineering, Nihon University, Koriyama, Fukushima 963-8642, Japan, E-mail: peng@mech.ce.nihon-u.ac.jp

(Received June 10, 2013, Revised July 14, 2013)

This paper reviews recent progress made toward modeling of cavitation and numerical simulation of cavitating water jets. Properties of existing cavitation models are discussed and a compressible mixture flow method for the numerical simulation of highspeed water jets accompanied by intensive cavitation is introduced. Two-phase fluids media of cavitating flow are treated as a homogeneous bubbly mixture and the mean flow is computed by solving Reynolds-Averaged Navier-Stokes (RANS) equations for compressible fluid. The intensity of cavitation is evaluated by the gas volume fraction, which is governed by the compressibility of bubble-liquid mixture corresponding to the status of mean flow field. Numerical results of cavitating water jet issuing from an orifice nozzle are presented and its applicability to intensively cavitating jets is demonstrated. However, the effect of impact pressure caused by collapsing of bubbles is neglected, and effectively coupling of the present compressible mixture flow method with the dynamics of bubbles remains to be a challenge.

cavitation, water jet, multi-phase flow, numerical simulation

Introduction

High-speed water jets in air or water have been widely utilized for burry removal and cleaning of complicated mechanical products, cutting of solid materials, and surface improvement of materials in various industry fields[1]. Among them, high-speed water jet injected into still water, which is called submerged water jet, has been applied to peening of metal material by using cavitation impacts caused by the collapse of cavitation bubbles[2,3]. It has received much attention also in environmental industry for the possibility of applications to decomposition of toxic substances and purification of sewages. Until now, many experimental studies on cavitating water jets have been made concerning jet driven pressure, shape and size of a nozzle, cavitation number etc.[4-6]. However, the structure of cavitating jet and the behavior of unsteady cavitation bubbles are still unclear for the difficulty to observe the interior of cavitating flows[7,8]. With the purpose of performance prediction and efficient design of high-speed water jet devices, much attention has been attracted to the numerical simulation of cavitating flows.

Cavitation usually takes place in low-pressure regions of relative high velocity and cavitating flows in most industrial applications are turbulent. The flow dynamics at the interface formed between liquid and gas phases involves complex bubble-bubble and bubble-liquid interactions. These interactions are not well understood in the closure region of cavities, where a distinct interface may not exist in the case of high void-fraction micro bubble cloud. In addition the near field of cavities reveals to be highly compressible due to the growth and collapse of bubbles while the far-field away from cavities is essentially incompressible. For the difficulty to consider all these different characteristics numerical simulations of cavitating flow have been conventionally carried out under certain simplifications such as inviscid and steady flows[9,10].

In this following, focusing on the numerical simulation of high-speed water jets accompanied by intensive cavitation we briefly summarize some numerical works related to modeling of cavitation and simulating of cavitating water jets. Then, we present a compressible mixture flow method based on a simplified estimation of bubble cavitation and its applicationto turbulent cavitating water jets issuing from a submerged orifice nozzle. Some numerical results are reported and its applicability to intensively activating jets is demonstrated.

1. Modeling of cavitating flow

Numerical methods used for treating cavitating flows may be classified into two categories: interface capturing methods and continuum modeling methods. The interface capturing methods assume that there is a clear and distinct interface between the liquid and gas phase, which can be determined via an iterative procedure. Their applications are limited to simpler problems where the cavity can be described as a well-defined closed volume of pure gas[11,12]. On the other hand, the continuum modeling methods do not make attempt to track the liquid-gas interface but treat the fluids media as a two-phase mixture whose density varies continuously between the liquid and vapor extremes. These methods are becoming more and more popular because they can be applied to turbulent flows often encountered in most industrial applications. The continuum methods are implemented using different approaches[13]: one-fluid methods, two-fluid methods, and hybrid methods.

The two-fluid methods assume that both phases co-exist at every point in the flow field and each phase is governed by its own set of conservation laws. So, the motions of liquid and bubbles are treated separately and two sets of governing equations derived for liquid and gas phases are solved interactively[14,15]. Usually, the volume change of bubbles is described by the Rayleigh-Plesset equation or similar ones and the exchanges of mass, momentum, and energy are estimated explicitly as transfer terms. Thus, these models can take into account the physical details occurring in the cavitation phenomenon. However, the transfer terms strongly depends upon the estimation of the interaction between the liquid and bubbles, which is very difficult since there is not a general physical model describing the interaction of liquid and bubbles. This kind of methods has been used for flows accompanying weak cavitation[16,17].

Differing from the two-fluid methods, the onefluid methods treat the fluid media of cavitating flows as a homogeneous fluid mixture by neglecting the velocity slip between the liquid and gas phases. The physical properties of the homogeneous mixture are determined according to the volume fraction of gas phase. So the fluid is pseudo-single phase one whose density may vary sharply over a range from liquid to gas one. For evaluation of the mixture density, Delannoy and Kueny[18]proposed a method to link directly the density to the static pressure and Iga et al.[19]improved it by using the equation of state for a locally homogeneous compressible two-phase medium under an equilibrium condition. In consideration for bubble dynamics, Kubota et al.[20]proposed a bubble two-phase cavitation model by coupling an incompressible flow solver with a simplified Rayleigh-Plesset equation describing the radial motion of bubble surface. Singhal et al.[21]developed a full cavitation model by estimating the temporal influence of mass transfer through an empirical formulation for the source term of gas void fraction transport. Although the one fluid approach cannot reproduce strong thermodynamic or kinetic non-equilibrium effects it is often used for its simplicity. Generally speaking, the computation of one-fluid homogeneous models is cheaper than that of two-fluid models because there is no need to treat the motion of a mass of bubbles separately.

The hybrid methods are intermediate ones between one-fluid and two-fluid methods. This kind of models has been developed by adding a mass equation for the gas or liquid density including a cavitation source term to the one-fluid methods[22-25]. The main difficulty of these models is related to the formulation of the cavitation source term and the tunable parameters involved in the vaporization and condensation process accompanying cavitation.

In addition to modeling cavitation, modeling of turbulence has been demonstrated to be another important issue affecting the numerical result of turbulent cavitating flow simulations. Some three-dimensional time-dependent computations obtained with Large Eddy Simulations (LES) or the Direct Numerical Simulations (DNS) have been reported but they are not yet tractable for general industrial applications. The Reynolds-Averaged Navier-Stokes (RANS) method is often applied by adopting a certain turbulence model to evaluate the unsteady turbulence effect according to the mean flow quantities[26]. However, the standard eddy-viscosity models based on the linear Boussinesq relation are known to suffer from numerous weaknesses. In particular, the over-production of eddy-viscosity reduces the development of unsteadiness and modifies the flow topology. For unsteady cavitating flows the problem of limiting the turbulent viscosity becomes determinant to capture oscillations of cavitation. Usually, arbitrary limiters are introduced in the turbulent viscosity calculation to obtain unsteady flow characteristics such as cavity shedding and re-entrant jet[27,28].

Another important aspect of cavitating flow simulations concerns the numerical schemes of CFD calculation. Cavitating flows are characterized by large variations in the local Mach number and the sonic speed in the liquid phase can be several orders of magnitude higher than that in the cavitation regions (supersonic regime). Thus, numerical methods for cavitating flows are required to treat both different flow regions of nearly incompressible (pure liquid) andhighly compressible (expanded bubbles) ones simultaneously, but it is demonstrated to be a hard work[29]. Usually, the category of incompressible flows requires an elliptic pressure-correction equation, and numerical methods such as SIMPLE or PISO pressure-based algorithms[24,30]must be modified to take into account finite acoustic speeds and compressibility effects in the cavitation regions. However, it may lead to an erroneous acoustic speed in the mixture, particularly in the interface region, which may be not appropriate for unsteady simulations[31]. Therefore, the compressibility of homogeneous fluid is often ignored in most works by considering the volume change caused by cavitation in a certain way[20,21]. On the other hand, compressible codes solve hyperbolic equations with time-marching algorithms require an equation of state to evaluate the pressure. A well-known problem concerns the stiffness on the solution convergence when the Mach number becomes low. In this situation, the dominance of convection terms renders the system stiff and compressible solvers converge slowly. To overcome this difficulty a preconditioned method[22]is necessary and the physical acoustic waves are usually replaced by pseudo-acoustic modes that are much closer to the advective velocity for reducing the stiffness and enhancing the convergence. Peng et al.[32-34]presented a flexible pressure-based procedure based on an improved CIP-CUP algorithm considering sharp declining of sonic speed in cavitation regions.

Fig.1 Comparison of computational result (upper pictures) and experimental data (lower pictures, from Ref.[43])

2. Bubble dynamics and cavitation impact

Cavitation is a strong unsteady phenomenon and its dynamics properties greatly depend upon the mutual interactions among cavitation bubbles[35,36]. Active utilizations of cavitation related to bubble collapse are recently extended to various fields such as ultrasound medical applications and drag delivery for cancer therapy[37]. To clarify the mechanism of cavitation phenomena it is important to understand the collapse and interaction of multiple bubbles. There are generally two approaches to the dynamics of a cluster of bubbles. One deals with the macroscopic motions of bubble cluster by using the continuum two-fluid method, in which evaluating of the mutual interactions among bubbles becomes a critical work. The other one is to analyze the microscopic motions of individual bubbles directly[38,39]by tracking the motion of all bubble surface. Takahira et al.[40]conducted a DNS for the collapse of two interacting bubbles in compressible liquid by an improved ghost fluid method and a strong shock wave formed in bubble collapsing was captured successfully.

Peng et al.[41]simulated the unsteady cavitation phenomenon of a bubble cloud caused by negative pressure pulse by applying the front tracking method[42]. The expanding and contracting of all bubbles are traced by taking into account the mutual interaction among them. Figure 1 shows expanding and contracting of the bubble cloud in a time sequence, where the outer layer bubbles in the simulation case are corresponding to the bubbles at the most outer layer in the experimental case. As shown in the figure computational results qualitatively agree to the experimental data obtained by Bremond et al.[43]. Micro liquid jets toward the inner bubbles formed in collapsing of bubble cloud and high impact pressure waves released under the effect of mutual interactions of bubbles are demonstrated clearly.

3. Modeling and simulation of high-speed cavitating water jet

The dynamics of submerged bubbles depends strongly on the surrounding pressure, temperature, and liquid surface tension. For clarifying the characteristics of growth, collapse, and rebound of a cavitation bubble travelling along the flow through a water jet nozzle, Alehossein and Qin[44]developed a densitybased method combined with a finite difference com-putation of the Rayleigh-Plesset equation governing the growth and collapse of a bubble under various pressure and temperature conditions. A variable time-step technique was applied to solve the highly nonlinear bubble oscillation equation by using the pressure and velocity data obtained from CFD analysis of jet flow as inputs[45]. However, the effect of bubble growth and collapse to the flow was neglected since the results of bubble dynamics computation were not taken back to the flow analysis. Peng et al.[25]presented a hybrid computation by combining the Rayleigh-Plesset equation with a compressible RANS computation, where the effect of bubble dynamics to the surrounding flow fields has been accounted by adding a source term related to the bubble radius to the RANS equations. The method demonstrated the possibility to predict the intensity of cavitation impact varying unsteadily together with flow field, but its application was limited to the cases of weak cavitation for the difficulty to fit the flow calculation to a severe variation of bubble radii in the case of intensive cavitation.

3.1 Modeling of cavitating water jets by a compressible mixture flow method

Aiming at the numerical simulation of intensively cavitating water jets, we developed a pressure–based compressible mixture flow method[28]. It was applied to unsteady cavitating flows issuing from a submerged nozzle under different cavitation numbers. A simplified estimation for the compressibility of homogeneous bubble-liquid mixture was proposed and the mean flow was calculated by RANS equations for compressible turbulent flow. Considering the characteristics of cavitating flow the set of equations was solved by applying the improved CIP-CUP algorithm[32]. The fluids media of cavitating flow are taken as a two-phase mixture of working liquid and cavitation bubbles and the density of the mixture is defined as follows by volume averaging.

where ρ denotes fluid density and α the volume faction. The subscripts L, G and M denote the liquid phase, the gas phase and the two-phase mixture, respectively. Then, the variation of mixture density is written as follows by taking the differential of above equation.

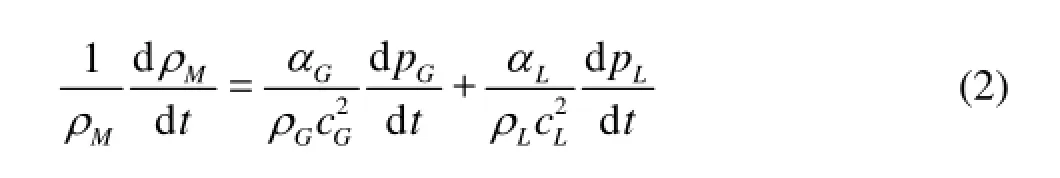
where c denotes the sonic speed and p does the working pressure. Considering the dynamic equilibrium in the radial direction across the interface of gas and liquid phases the pressure jump from the interior to the exterior of a bubble can be given as follows

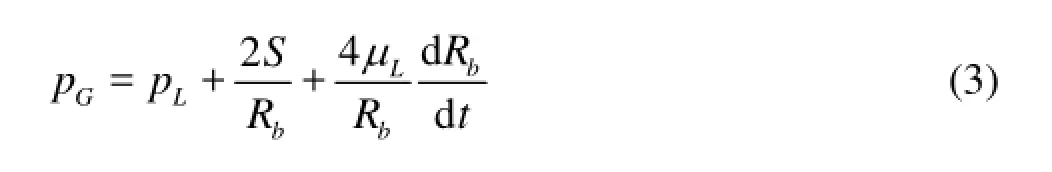
whereLμ denotes the liquid viscosity and S does the surface tension coefficient.bR denotes the mean bubble radius in a local area, which can be estimated by solving the Rayleigh-Plesset equation for the motion of bubble surface[35]. However, it is very time consuming since the frequency of bubble oscillation is quite different with that of flow field variation. Considering the practice of engineering applications a simplified relation, dpG/dt≈dpL/dt , is adopted here by neglecting the instantaneous variation of bubble radius. Then the variation of mixture density is directly related to the liquid pressure.

Thus, the average sonic speed in the two-phase mixture is defined as follows approximately.

Concerning sonic speed in the fluid mixture both the liquid and the gas included in bubbles are supposed to work exponentially and the state equations are used to relate their density and working pressure. Then, the compressibility of liquid and gas phases is written below, similarly.

where the subscript =Lκ, G, respectively denotes the liquid and gas phases. n denotes the ratio of specific heat and B is a constant, which is given to be 3.049×108Pa for liquid and 0 for gas. Corresponding to the sharp variation of surrounding liquid pressure cavitation bubbles expand and contract greatly at a high frequency and then the density of bubble-liquid mixture varies greatly. Thus, the compressibility of cavitating mixture varies much intensively compared to that of non-cavitating bubbly mixture.

As flow governing equations for the compressible two-phase fluid mixture, RANS equations for compressible turbulent flow are adopted and the temperature variation caused by cavitation is supposed to be very small. Thus conservation equations of mass and momentum are employed together with the density-pressure relation of the mixture, and the transportation equation of gas mass fraction is used to esti-mate its volume fraction. The flow turbulence is evaluated by using the RNG kε- model[46]for high Reynolds number flow. Corresponding to expanding and contracting of cavitation bubbles in cavitating flow the turbulence energy of bubbly flow may be absorbed, and the eddy viscosity in cavitating region becomes much weak compared to the liquid flow region. Thus, a modification of eddy viscosity show below is introduced to take account of the effect of cavitation on the flow turbulence[28].

where tμ denotes the eddy viscosity, k and ε do the turbulence energy and the turbulence dissipation rate. Cμis a constant of turbulence model. χ is a modification coefficient given as follows.

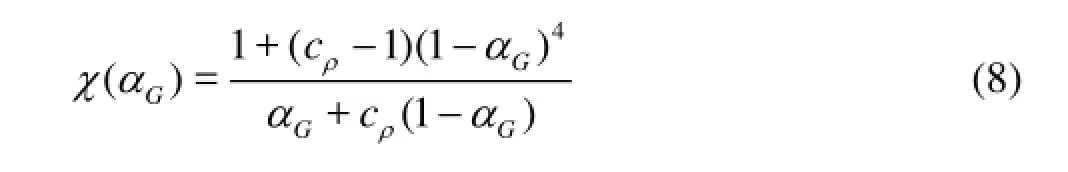
in which cρ=ρL/ρG. k and ε are then solved by their transportation equations.

3.2 Behavior of cavitating cloud in submerged water jets issuing from an orifice nozzle

Water jets issuing from a sharp-edged circular orifice are treated under different cavitation numbers. Geometry of the orifice are given to be that /=Dd 2.88 and /=Ld5.0, where D, d and L denote the inlet diameter, the throat diameter, and the orifice length, respectively. As an index for the similarity of cavitation dynamics[1,47,48], the cavitation number σ is usually defined as follows for submerged water jets.

whereinP denotes the jet driving pressure,op the static surrounding pressure at the nozzle exit and pv(T∞) the saturated vapor pressure at the reference temperature T∞.

Figure 2 shows, as a sample, the development of a cavitating jet of which the cavitation number σ= 0.1 and the jet driven pressure Δp≅1.0MPa . Figure 2(a) to 2(d) present the contour maps of gas volume fraction in a sequence time, where αGincreases to 0.8 locally with developing of jet flow. As shown in Fig.2(a) cavitation takes place initially at the entrance of nozzle throat as well as the central area of starting vortex near the nozzle exit. According to Fig.2(b) to 2(d) we understand thatGα increases gradually and cavitation bubbles mainly concentrate in the shear between the main jet and surrounding water.

Fig.2 Development of cavitating water jet (σ=0.1)

Fig.3 Distribution of cavitating jets at different cavitation numbers

Figure 3 shows the flow distribution of developed activating jets under different cavitation numbers. Comparing the result, we may confirm that while σequals 2.0 the value ofGα is almost zero everywhere and no cavitation takes place. When the cavitation number is decreased from 0.1 to 0.02 the maximum value ofGα, which indicates the local intensity of cavitation, keeps almost the same. However, the area of strong cavitation denoted by high value of gas volume fraction increases with the decrease of cavitation number. The discharge coefficients under different cavitation numbers were evaluated also, and it is demonstrated that the discharge coefficient decreases to 85% approximately compared to the case of no-cavitating jets when σ is decreased 0.1[1]. The result agrees with Nurick’s experiment data[48]and the reliability of numerical simulation has been confirmed.

3.3 Issues and perspectives on the numerical simulation of cavitating water jet

The result shown in Fig.3 demonstrates that the present compressible mixture flow method may successfully capture the unsteady behavior of cavitation cloud. The method is useful to estimate the global property of a cavitating flow field. However, as stated above the inner pressure of cavitation bubbles depends on not only the surrounding liquid pressure but also the acceleration of bubble interface. In the preceding computation, the temporal variation of inner gas pressure is substituted with that of the outer liquid pressure for the purpose to reduce computation time. Thus, the propagation of pressure wave in the local area of bubble cloud cannot be captured correctly and the effect of impact pressure caused by collapsing of bubbles is completely disregarded. To evaluate the dynamic property such as the strength of impact pressure of cavitatng flows, effectively coupling of the present compressible mixture flow method with the dynamics of bubbles remains to be a great challenge. Usually, the frequency of bubble oscillation is very high compared to the temporal variation of flow field and a proper simulation of such complex flow system is very time consuming[25].

As for cavitation bubble dynamics, the effect of cavitation is usually estimated by solving the Rayleigh-Plesset equation or revised ones governing the mean radius of a bubble cluster in a computation cell. Then, definitions of the surrounding liquid pressure and the inner pressure of the representative bubble become a critical issue. For this reason, Fuster and Colonius[49]derived an extended Rayleigh-Plesset equation in which the infinite liquid pressure around the representative bubble of a cell is defined by accounting influences of other bubbles and local cell size. The method has been used to treat a weak activating flow only, but is expectable to be applied to intensive cavitating flow by improving the flexibility of the model.

On the other hand, the direct numerical simulation by surface tracking method reproduces the microscopic motions of individual bubbles under the interaction of multiple bubbles. It is very helpful to understand the physics of bubble cloud cavitation, especially the mechanism of extremely high impact pressure releasing at collapsing of bubbles. At the same time, it is also very convenient to evaluate the effect of mass and heat transfer such as condensation and evaporation occurring at the bubble surface. The method treats cavitating flows from a microscopic view and is difficulty to be applied to practical engineering flows for the problem of computation cost. In order to take the advantages of both these two kinds of methods to exactly reproduce the physic process of intensive cavitation research and development of new multi-scale approaches[50]coupling the indirect modeling method and the direct front tracking method is desired for the numerical simulation of high speed cavitating jets.

4. Summary

Expanding and collapsing of bubbles is an important matter needs to be carefully considered in the numerical analysis of cavitating flows. This paper reviews recent progress made toward modeling of cavitation and numerical simulation of high-speed cavitating water jets. Properties of existing cavitation models including bubble dynamics effect and turbulence closures are discussed, and then a compressible mixture flow method based on a simplified estimation of bubble cavitation is introduced focusing on the numerical simulation of high-speed water jets accompanied with intensive cavitation.

High-speed water jets issuing from a submerged orifice nozzle have been treated by the method and its applicability to intensively cavitating water jets has been confirmed. The results demonstrate that: (1) Cavitation takes place initially at the entrance of orifice and cavitation bubbles mainly concentrate in the shear layer surrounding the jet. (2) The intensity of cavitation increases with decreasing of the cavitation number.

However, the effect of impact pressure releasing at collapsing of bubble cloud is disregarded in the present work and effectively coupling of the present compressible mixture flow method with the bubble dynamics remains to be a challenge. For investigating the physical mechanism of intensively cavitating water jets, research and development of new multi-scale approaches combining the indirect modeling method and the direct front tracking method are desired.

Acknowledgement

This work was supported by the Japan Society for the Promotion of Science (JSPS), Grant-in-Aid for Scientific Research (C) (Grant No. 22560177).

References

[1] SHIMIZU S., PENG G. Water jetting technology for LOHAS[M]. Tokyo, Japan: International Academic Printing Co. Ltd., 2009, 294.

[2] SOYAMA H., KUSAKA T. and SAKA M. Peening by the use of cavitation impacts for the improvement of fatigue strength[J]. Journal of Materials Science Letters, 2001, 20(13): 1263-1265.

[3] SOYAMA H., TAKAKUWA O. Enhancing the aggressive strength of a cavitating jet and its practical application[J]. Journal of Fluid Science and Technology, 2011, 6(4): 510-521.

[4] YAMAGUTI A., SHIMIZU S. Erosion due to impingement of cavitation jet[J]. Journal of Fluids Engineering, 1987, 109(4): 442-447.

[5] SOYAMA H., YANAUCHI Y. and SATO K. et al. High-speed observation of ultrahigh-speed submerged water jets[J]. Experimental Thermal and Fluid Science, 1996, 12(4): 411-416.

[6] FOLDYNA J., SITEK L. and SVEHLA B. et al. Utilization of ultrasound to enhance high-speed water jet effects[J]. Ultrasonics Sonochemistry, 2004, 11(3): 131-137.

[7] OOI K. K. Scale effects on cavitation inception in submerged water jets: A new look[J]. Journal of Fluid Mechanics, 1985, 151: 367-390.

[8] GOPALAN G., KATZ J. and KNIO O. The flow structure in the near field of jets and its effect on cavitation inception[J]. Journal of Fluid Mechanics, 1999, 398: 1-43.

[9] FRANC J. P., MICHEL J. M. Attached cavitation and the boundary layer: Experimental investigation and numerical treatment[J]. Journal of Fluid Mechanics, 1985, 154: 63-90.

[10] LEMONNIER H., ROWE A. Another approach in modeling cavitation flows[J]. Journal of Fluid Mechanics, 1988, 195: 557-580.

[11] SUSSMAN M. A second order coupled level set and volume-of-fluid method for computing growth and collapse of vapor bubbles[J]. Journal of Computational Physics, 2003, 187(1): 110-136.

[12] YU P., CECCIO S. L. and TRYGGVASON G. The collapse of a cavitation bubble in shear flows -A numerical study[J]. Physics of Fluids, 1995, 7(11): 2608-2616.

[13] GONCALVES E., PATELLA R. F. Numerical simulation of cavitating flows with homogeneous models[J]. Computers and Fluids, 2009, 38(9): 1682-1696.

[14] SAUREL R., LEMETAYER O. A multiphase model for compressible flows with interfaces, shocks detonation waves and cavitation[J]. Journal Fluid Mechanics, 2001, 431: 239-271.

[15] YANO T., EGASHIRA R. and FUJIKAWA S. Linear analysis of dispersive waves in bubbly flows based on averaged equations[J]. Journal of Physical Society of Japan, 2006, 75(10): 104401.

[16] MATSUMOTO Y., YOSHIZAWA S. Behaviour of a bubble cluster in an ultrasound field[J]. International Journal of Numerical Methods in Fluids, 2004, 47(6): 591-601.

[17] TAMURA Y., MATSUMOTO Y. Improvement of bubble model for cavitating flow simulations[J]. Journal of Hydrodynamics, 2009, 21(1): 41-46.

[18] DELANNOY Y., KUENY J. Two phase flow approach in unsteady cavitation modeling[C]. Cavitation and multiphase flow forum. 1990, ASME FED-Vol. 98, 153-158.

[19] IGA Y., NOHMI M. and GOTO A. et al. Numerical study of sheet cavitation breakoff phenomenon on a cascade hydrofoil[J]. Journal of Fluids Engineering, 2003, 125(4): 643-651.

[20] KUBOTA A., KATO H. and YAMAGUTI H. A new modeling of cavitating flow: A numerical study of unsteady cavitation on a hydrofoil section[J]. Journal of Fluid Mechanics, 1992, 240: 59-96.

[21] SINGHAL A. K., ATHAVALE M. M. and LI H. et al. Mathematical basis and validation of the full cavitation model[J]. Journal of Fluids Engineering, 2002, 124(3): 617-624.

[22] KUNZ R. F., BOGER D. A. and STINEBRING D. R. et al. A preconditioned Navier-Stokes method for twophase flows with application to cavitation prediction[J]. Computers and Fluids, 2000, 29(8): 849-875.

[23] HSIAO C. T., CHAHINE G. Prediction of tip vortex cavitation inception using coupled sphericaland nonspherical bubble models and Navier-Stokes computations[J]. Journal of Marine Science and Technology, 2004, 8(3): 99-108.

[24] SENOCAK I., SHYY W. A pressure-based method for turbulent cavitating flow computations[J]. Journal of Computational Physics, 2002, 176(2): 363-383.

[25] PENG G., EGASHIRA R. and YANO T. et al. A compressible two-phase flow bubble cavitation model for computation of cavitating flows[C]. Proceedings of the 1st International Colloquium on Dynamics, Physics and Chemistry of Bubble and Gas-Liquid Boundaries. Hokkaido, Japan, 2007.

[26] WILCOX D. C. Turbulence modeling for CFD[M]. 2nd Edition, La Canada, California, USA: DCW Industries, Inc., 2002, 540.

[27] DELGOSHA C. O., REBOUD J. L. and DELANNOY Y. Numerical simulation of the unsteady behaviour of cavitating flows[J]. International Journal of Numerical Methods in Fluids, 2003, 42(5): 527-548.

[28] PENG G., SHIMIZU S. and FUJIKAWA S. Numerical simulation of cavitating water jet by a compressible mixture flow method[J]. Journal of Fluid Science and Technology, 2011, 6(4): 499-509.

[29] YABE T., WANG P.-Y. Unified numerical procedure for compressible and incompressible fluid[J]. Journal of Physical Society of Japan, 1991, 60(7): 2105-2108.

[30] VENTIKOS Y., TZABIRAS G. A numerical method for the simulation of steady and unsteady cavitating flows[J]. Computers and Fluids, 2000, 29(1): 63-88.

[31] AHUJA V., HOSANGADI A. and ARUNAJATESAN S. Simulations of cavitating flows using hybrid unstructured meshes[J]. Journal of Fluids Engineering, 2001, 123(4): 331-340.

[32] PENG G., ISHIZUKA M. and HAYAMA S. An improved CIP-CUP method for submerged water jet flow simulation[J]. JSME International Journal Series B, 2001, 44(4): 497-504.

[33] PENG G., FUJIKAWA S. and ISHIZUKA M. et al. Numerical simulation of submerged water jet by an Improved CIP-CUP method[J]. Computational Fluid Dynamics Journal, 2002, 11(1): 27-34.

[34] PENG G., EGASHIRA R. and YANO T. et al. A pressure-based two-phase flow method for computation of bubble cavitation flows[C]. Proceedings of 5th Joint ASME/JSME Fluids Engineering Conference. San Diego, USA, 2007.

[35] BRENNEN C. E. Cavitation and bubble dynamics[M].New York, USA: Oxford University Press, 1995.

[36] LI S. C. Cavitation of hydraulic machinery[M]. Singapore: World Scientific Publishing Co., 2001, 464.

[37] MATSUMOTO Y., ALLEN J. S. and YOSHIZAWA S. et al. Medical ultrasound with microbubbles[J]. Experimental Thermal and Fluid Science, 2005, 29(3): 255-265.

[38] POPINET S., ZALESKI S. Bubble collapse near a solid boundary: A numerical study of the influence of viscosity[J]. Journal of Fluid Mechanics, 2002, 464: 137-163.

[39] DABIRI S., SIRIGNANO W. A. and JOSEPH D. D. Interaction between a cavitation bubble and shear flow[J]. Physics of Fluids, 2010, 22(4): 042102.

[40] TAKAHIRA H., MATSUNO T. and SHUTO K. Numerical investigations of shock-bubble interactions in mercury[J]. Fluid Dynamics Research, 2008, 40(7): 510-520.

[41] PENG G., SHIMIZU S. and TRYGGVASON G. Numerical simulation of bubble cloud cavitation by front-tracking method[C]. Proceedings of the 26th CFD Symposium. Tokyo, Japan, 2012(in Japanese).

[42] TRYGGVASONA G., BUNNER B. and ESMAEELI A. et al. A front-tracking method for the computations of multiphase flow[J]. Journal of Computational Physics, 2001, 169(2): 708-759.

[43] BREMOND N., ARORA M. and OHL C.-D. et al. Controlled multi-bubble surface cavitation[J]. Physics Review Letters, 2006, 96: 224501.

[44] ALEHOSSEIN H., QIN Z. Numerical analysis of Rayleigh-Plesset equation for cavitating water jets[J]. International Journal of Numerical Methods in Engineering, 2007, 72(7): 780-807.

[45] QIN Z., BREMHORST K. and ALEHOSSEIN H. Simulation of cavitation bubbles in a convergent–divergent nozzle water jet[J]. Journal of Fluid Mechanics, 2007, 573: 1-25.

[46] YAKHOT V., ORSZAG S. A. and THANGAM S. et al. Development of turbulence models for shear flows by a double expansion technique[J]. Physics of Fluids, 1992, 4(7): 1510-1520.

[47] SOU A., HOSOKAWA S. and TOMIYAMA A. Effects of cavitation in a nozzle on liquid jet atomization[J]. International Journal of Heat and Mass Transfer, 2007, 50(18): 3575-3582.

[48] NURICK W. H. Orifice cavitation and its effect on spray mixing[J]. Journal of Fluids Engineering, 1976, 98(4): 681-687.

[49] FUSTER D., COLONIUS T. Modelling bubble clusters in compressible liquids[J]. Journal of Fluid Mechanics, 2011, 688: 352-389.

[50] DEEN N. G., ANNALAND M. S. and KUIPERS J. A. M. Multi-scale modeling of dispersed gas-liquid twophase flow[J]. Chemical Engineering Science, 2004, 59(8): 1853-1861.

10.1016/S1001-6058(11)60389-3

* Biography: PENG Guoyi (1964), Male, Ph. D., Professor