Radiation and diffraction analysis of a cylindrical body with a moon pool*

ZHOU Hua-wei (周华伟)

State Key Laboratory of Ocean Engineering, College of Naval Architecture, Ocean and Civil Engineering,

Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: zhouhuawei1010@hotmail.com

ZHANG Hong-sheng (张洪生)

Ocean Environmental and Engineering College, Shanghai Maritime University, Shanghai 201306, China

Radiation and diffraction analysis of a cylindrical body with a moon pool*

ZHOU Hua-wei (周华伟)

State Key Laboratory of Ocean Engineering, College of Naval Architecture, Ocean and Civil Engineering,

Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: zhouhuawei1010@hotmail.com

ZHANG Hong-sheng (张洪生)

Ocean Environmental and Engineering College, Shanghai Maritime University, Shanghai 201306, China

(Received May 22, 2012, Revised July 19, 2012)

An analytical solution is presented for the radiation and the diffraction of a cylindrical body with a moon pool floating on the surface of water with a finite depth. The expressions for the potentials are obtained by the method of separation of variables, and the unknown coefficients are determined by the boundary conditions and the matching requirements on the interface. The effects of the moon pool on the hydrodynamic characteristics of the body are investigated. Some peaks are observed on the curves of the added mass and damping coefficients, corresponding to the resonant frequencies of the moon pool. The internal free surface moves like a piston at a certain low resonant frequency.

radiation and diffraction, cylindrical body, moon pool, variable separation method, resonant frequencies

Introduction

Over the last few decades, with the mushrooming of offshore marine structures, the hydrodynamics of the cylindrical body with a moon pool has attracted a great attention. This geometric configuration represents a generic shape of a variety of ocean facilities and finds a wide range of applications. One of the typical examples is the classical spar platform, consisting of a vertical cylindrical hull with a centre well for storage purposes or protecting risers. Furthermore, it is also the characteristic feature of some drilling ships and wave power devices. Through the opening at the bottom, the sea water flows into the moon pool and some complex internal motions would ensue. Compared with the bottomless cylindrical body shown in Mavrakos[1], the moon pool has a number of resonant frequencies. When the frequency of the incident wave or the motion of the body is close to one of these frequencies, the piston or sloshing motion would occur, which will induce a large motion of the structures and further affect their integrity. This problem has an important bearing on the fundamental properties of this body, especially the complex behaviours of the moon pool.

Generally speaking, there are two basic approaches to analyze the hydrodynamic characteristics of floating bodies. The frequency domain method is usually employed to calculate the added mass, the damping coefficients and the excitation forces, to predict the response of the body to the wave and the current, as used by Tao et al.[2], Sadeghi et al.[3], Lee et al.[4], Taghipour and Moan[5]and others. However, for some time dependent dynamic behaviours of the body, such as the coupled effects among the mooring lines, the moon pool and other components, the frequency domain method will lead to low accuracy and bring in some errors. To study their effects on the performance of the floating body, one has to adopt an alternative approach, the time domain method, as used by Ma and Patel[6], Agarwal and Jain[7], Koo et al.[8], Zhang et al.[9], and others.

However, in this paper, we are interested in the mechanism of the moon pool, without considering the effects of mooring lines and other components. The time domain solutions would be expensive and provide little insight into the nature of the moon pool. With the cylindrical geometry of the body, the method of separation of variables in the framework of thelinear potential theory is definitely an efficient and economical way. This method was adopted by Garrett[10], Zhu and Mitchell[11,12], Mavrakos[1,13]to study the radiation and diffraction problems for thin or thick-walled bottomless cylindrical bodies. But, the influence of the partially closed bottom plate is not appropriately considered, and it is usually used in the spar platform and drilling ship.

Due to the existence of the holed plates at the bottom, the hydrodynamic properties of the body may be different from those of bottomless bodies, especially in the vicinity of resonant frequencies. In view of this, this paper uses the method of separation of variables to study the linear hydrodynamic characteristics of a thick-walled cylindrical body with a moon pool floating on the water surface of finite depth. Specifically, the whole fluid domain is divided into four coaxial ring-shaped domains. The velocity potential in each sub-domain is expanded into a series based on the method of separation of variables. The expansion satisfies the governing equation, the radiation condition and the boundary conditions along the horizontal plan. The remaining boundary conditions and the continuity of the velocity and the pressure on the interfaces of the sub domains are used to obtain the unknown coefficients in the expansion. Based on this procedure, the effects of the holed bottom and the wall thickness of the body on the added mass and the damping coefficients can be revealed. The resonance inside the moon pool will also be studied.

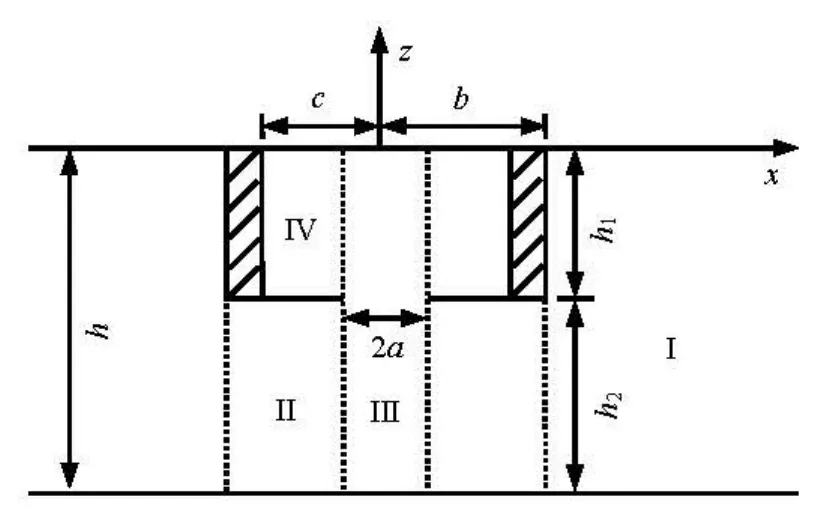
Fig.1 Sketch of the problem of a floating body with a cylindrical moon pool

1. Governing equation and boundary conditions

We consider a thick-walled cylindrical body with the external radiusb , the internal radiuscand the draughth1, floating on the free surface. The body has a concentric hole of radiusa at its bottom (see Fig.1). The depth of the open water outside the body is h, which means the distance between the bottom of the body and the bottom of the liquid is h2=h-h1. A cylindrical coordinate system orθ zis used, in whichorθis on the still water level and zaxis points upwards and passes through the centre of the body.

Assuming that the fluid is incompressible and inviscid, the flow is irrotational and the motion is small, the fluid flow can be described by the linearized velocity potential theory. When the motion is periodic with frequencyω, the total velocityΦcan be expressed as

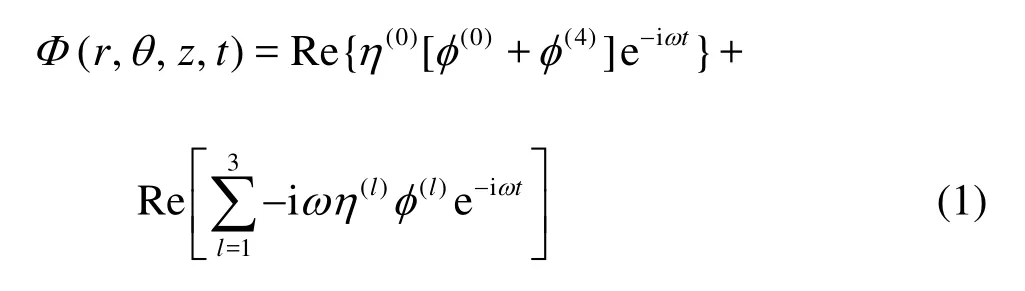
where Re means the real part of a complex function, i=,φ(0)and φ(4)are the spatial velocity potentials due to the incident and diffracted waves, and η(0)is the incoming wave amplitude,φ(l)(l=1,2,3) are the spatial velocity potentials corresponding to the surge (horizontal), heave (vertical) and pitch (rotational) motions, respectively, and η(l)(l=1,2,3)are the corresponding motion amplitudes. Due to the symmetrical configuration of the present body, the sway and roll modes are not considered here. Additionally, the yaw motion about thezaxis does not create any fluid motion and is omitted here too. Each of these complex spatial potentialsφ(l)(l=1,...,4)satisfies the Laplace equation,

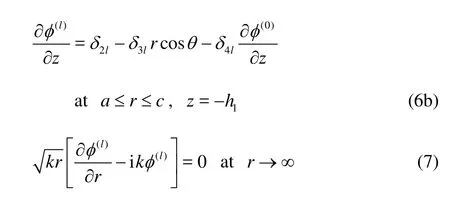
where v=ω2/g , the point at r =0and z=0is assumed to be the centre of rotation,δjlis the Kronecker delta function given by

In the above equation,φ(0)represents an incident wave propagating in the positivexdirection and can be written as

2. Solution procedure

To solve the above boundary value problem analytically, the fluid domain can be divided into four regions as depicted in Fig.1, which are I (b≤r≤∞, -h≤ z≤0), II (a ≤ r≤ b, - h ≤ z ≤-h1), III(r≤a, -h≤ z≤0)and IV (a ≤r≤ c, - h1≤z≤0), respectively. The corresponding potential in each domain is distinquished by subscripts1to4. Based on the method of separation of variables and taking into account some of the boundary conditions, the potential in each domain can be expressed as

We may notice that the above expansions satisfy the boundary conditions on all the horizontal planes. For this reason, the particular solutions φ(l)are defined as

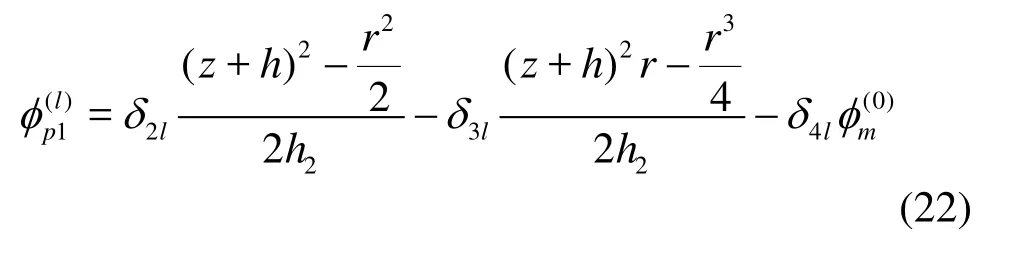
Equation (38) can be solved by the Gauss elimination method or some other iteration method.

Once the velocity potentials are known, the hydrodynamic force on the body can be obtained from the integration of the pressure based on the linear Bernoulli equation over the wetted body surface. For the radiation force due to the body oscillation per unit amplitude, we have

where Sbis the wetted body surface,n1= nx,n2= nzandn3= znx-xnz,nis the unit inward normal of the body surface with nxand nzbeing its components in thexandzdirections, respectively.

The force due to the wave radiation can also be written in terms of the added mass µijand the damping coefficientλij. They can be non-dimensionalized as follows:

3. Results and discussions

In the numerical simulation, unless otherwise stated, the geometrical parameters are h/ b =3.0,h1/ b =1.0,a/ b =0.2and c/ b=0.5.

3.1 Verification

Fig.2 Wave excitation force by the method of direct integration and the Haskind relationship

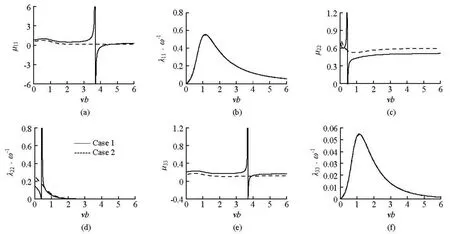
Fig.3 Added mass and damping coefficients of a cylinder with moon pool and an intact cylinder

where Cgis the group velocity and Ai(π)is the complex wave amplitude asr→∞, due to the body motion at the modei , which can be obtained from Eq.(12) as

The wave excitation force calculated by the method of the direct integration of Eq.(43) and the Haskind relationship in Eq.(44) are plotted in Fig.2. The good agreement between them indicates the correctness of the present solution.

Fig.4 Free surface elevation inside the moon pool around vb≈0.425

3.2 Resonant behaviours

Fig.5 Added mass and damping coefficients of body with hole of a/ b =0.1, 0.25, 0.4

where κnis the root of J1′(κnc )=0. When n =1, the first natural frequency of the sloshing modes in the present cylindrical tank is v1=3.678, which is close to vb≈3.675 and can be used to explain the peaks in Figs.3(a) and 3(e).

As for the symmetrical mode, both the added mass and the damping coefficient of the present body are different from those of an intact cylinder. Specifically, for Case 1, the peaks of µ22and λ22occur at vb≈0.425 in Figs.3(c) and 3(d), which might be the response of the piston motion. To confirm it, we consider the wave elevation ζ(2)inside the moon pool, which can be expressed as

The results alongx axis at vb =0.40,0.425and 0.45are plotted in Fig.4, which are non-dimensionalized by η(2). It is observed that the whole free surface moves up and down together and the piston mode is evident.

3.3 Effect of the size of the opening at the bottom

To investigate the effect of the size of the opening at the bottom, three cases are considered, including a/ b =0.1,a/ b =0.25and a/ b =0.4. The other geometrical parameters are h/ b =3.0, h1/b=1.0 and c/ b =0.5. The added mass and the damping coefficients are shown in Fig.5. Some peaks are found in the curves, which are related to the resonant behaviors discussed above. It can be seen that the size of the opening does not affect the behaviors of the hydrodynamic coefficients for the asymmetrical modes. Specifically, in Figs.5(a) and 5(e), the peaks of µ11in the surge motion and µ33in the pitch motion at different a/ b all occur atvb≈3.675, which is close to the first resonant frequency of the cylindrical tank. This also indicates that the first resonant frequency of the sloshing motions in the present body is not affected by the size of the opening and can be predicted by Eq.(46) approximately.

However, for the heave motion, the size of the opening affects the added mass and the damping coefficients significantly. As shown in Figs.5(c) and 5(d), the peaks of µ22and λ22occur atvb≈0.25,0.55, 0.675for a/ b =0.1,0.25,0.4, respectively. It is clearly show n that, with the increase of the size of the opening,theresonantfrequency for the piston motiontends to increase, while the amplitudes of the corresponding hydrodynamic coefficients decrease dramatically.

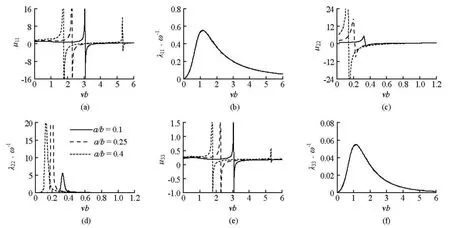
Fig.6 Added mass and damping coefficients of body with wall thickness of c/ b =0.6, 0.8, 1.0

3.4 Effect of the wall thickness of the body

It is also interesting to investigate the effect of the wall thickness of the body, which is related to the inner radius c and can be denoted byb-c. Three cases withc/ b =0.6,0.8and1.0are considered and other geometrical parameters areh/ b =3.0,h1/ b =1.0 and a/ b=0.2. The added mass and the damping coefficients are plotted in Fig.6. As shown in Figs.6(a) and 6(e), the peaks ofµ11for the surge motion and µ33for the pitch motion occur regularly, which can be predicted by Eq.(46) approximately. More significantly, it is found in Figs.6(c) and 6(d) that the peaks ofµ22and λ22for the heave motion are affected by the wall thickness too. With the decrease of the wall thickness, the resonant frequency for the piston mode becomes smaller.

4. Conclusions

The radiation and the diffraction of a thickwalled cylindrical body with a moon pool are studied by an analytical solution procedure based on subdividing the fluid domain and the method of variable separation. The results are verified through the relationship between the radiation and the diffraction problems. The resonant behaviors are found in all motions of the present body. The resonant frequencies for the surge and pitch modes are similar to the sloshing frequencies of a cylindrical tank, which are hardly affected by the opening at bottom while they occur regularly with the variation of the wall thickness. The piston-like motion is found in the heave mode at a special low frequency, which is significantly affected by both the opening at bottom and the wall thickness.

The present problem is studied in the frequencydomain based on the linear potential theory. Some time-domain methods are suggested to consider more details of the nonlinearity of the present problem.

Acknowledgements

This work was supported by the Lloyd’s Register Educational Trust (LRET) through the joint centre involving University College London, Shanghai Jiao Tong University and Harbin Engineering University, to which the authors are most grateful. The LRET is an independent charity institution working to achieve advances in transportation, science, engineering and technology education, training and research worldwide for the benefit of all people.

[1] MAVRAKOS, S. A. Hydrodynamic coefficients for a thick-walled bottomless cylindrical body floating in water of finite depth[J]. Ocean engineering, 1988, 15(3): 213-229.

[2] TAO L., LIM K. Y. and THIAGARAJAN K. Heave response of classic spar with variable geometr[J]. Journal of Offshore Mechanics and Arctic Engineering, 2004, 126(1): 90-95.

[3] SADEGHI K., INCECIK A. and DOWNIE M. J. Response analysis of a truss spar in the frequency domain[J]. Journal of Marine Science and Technology, 2004, 8(3): 126-137.

[4] LEE H. H., WONG S. H. and LEE R. S. Response mitigation on the offshore floating platform system with tuned liquid column damper[J]. Ocean engineering, 2006, 33(8-9): 1118-1142.

[5] TAGHIPOUR R., MOAN T. Efficient frequency-domain analysis of dynamic resonponse for the multi-body wave energy converter in multi-directional waves[C]. Proceedings of the Eighteenth Intertional Offshore and Polar Engineering Conference. Vancouver, BC, Canada, 2008.

[6] MA Q. W., PATEL M. H. On the non-linear forces acting on a floating spar platform in ocean waves[J]. Applied Ocea Research, 2001, 23(1): 29-40.

[7] AGARWAL A. K., JAIN A. K. Nonlinear coupled dynamic response of offshore spar platforms under regular sea waves[J]. Ocean engineering, 2003, 30(4): 517-551.

[8] KOO B. J., KIM M. H. and RANDALL R. E. Mathieu instability of a spar platform with mooringand risers[J]. Ocean engineering, 2004, 31(17-18): 2175-2208.

[9] ZHANG Fan, YANG Jian-min, LI Rui-pei et al. Numerical investigation on the hydrodynamic performances of a new spar concept[J]. Journal of Hydrodynamics, Ser. B, 2007, 19(4): 473-481.

[10] GARRETT C. J. R. Bottomless harbours[J]. Journal of Fluid Mechanics, 1970, 43(3): 433-449.

[11] ZHU S., MITCHELL L. Diffraction of ocean waves around a hollow cylindrical shell structure[J]. Wave Motion, 2009, 46(1): 78-88.

[12] ZHU S., MITCHELL L. Combined diffraction and radiation of ocean waves around an OWC device[J]. Journal of Applied Mathematics and Computing, 2011, 36(1-2): 401-416.

[13] MAVRAKOS S. A. Hydrodynamic coefficients in heave of two concentric surface-piercing truncated circular cylinders[J]. Applied Ocean Research, 2005, 26(3-4): 84-97.

[14] CHAKRABARTI S. K. Handbook of offshore engineering[M]. London, UK: Elsevier, 2005.

[15] LINTON C. M., MCLVER P. Handbook of mathematical techniques for wave/structure interactions[M]. London, UK: CRC Press, 2001.

10.1016/S1001-6058(13)60354-6

* Biography: ZHOU Hua-wei (1984-) Male, Ph. D. Candidate

ZHANG Hong-sheng,

E-mail: hszhang@shmtu.edu.cn