BP神经网络在轧制力计算中的应用

夏 宇，赵团民，郭 军

(1.中国重型机械研究院股份公司，陕西 西安 710032;2.西安交通大学，陕西 西安 710049)

0 前言

人工神经网络是20世纪40年代来发展起来的一门交叉学科，它以分布方式来存储知识，以并行方式进行处理，具有强大的容错能力，而且还具有很好的自适应和自学习功能，能用于逼近任意复杂的非线性系统，冷轧带钢轧制力的计算即属于此类问题。轧制力的精确计算对制订合理的轧制规程和提高产品质量都有重要意义。BP神经网络是人工神经网络的一种重要类型，本文将应用BP神经网络对轧制力进行计算分析。

人工神经网络是人类在大脑神经网络认识理解的基础上，人工构造的能够实现某些功能的神经网络。它是理论化的人脑神经网络的数学模型，是基于模拟大脑神经网络结构和功能来建立的一种信息处理系统，它事实上是由大量的简单元件相互连接形成的复杂网络，能表现出复杂非线性系统的特性，它可以处理一些环境信息复杂、知识背景不清楚、推理规则尚不明确的问题。

一般而言，人工神经网络和经典计算方法相比并非在所有问题上都显得优越，只有当常规方法解决不了或解决效果不佳时，人工神经网络方法才能显示出其优越性。尤其对问题的机理不甚了解或不能用数学模型表示的系统，如故障诊断、特征提取和预测等问题，人工神经网络往往是最有利的工具。另一方面，人工神经网络对处理大量原始数据而不能用规则或公式描述的问题，表现出极大的灵活性和自适应性。

几十年来，提出了轧制力的计算的许多数学模型和经验公式，但这些计算公式中的参数如摩擦系数和变形抗力很难精确的测定，同时经过验证，公式只有在某些道次中的计算误差较小，某些道次中的误差极大，这说明数学模型对轧制过程的描述是不全面，有缺陷的。另一方面，通过工厂的实际生产积累了大量的实测数据，这些实测数据需要通过良好的方法加以分析，提取出有价值的信息细节，而这正是人工神经网络的强项。

BP神经网络是一种多层前馈神经网络，该网络的主要特点是信号前向传递，误差反向传播。在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层。每一层的神经元状态只影响下一层神经元状态。如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络权值和阈值，从而使BP神经网络预测输出不断逼近期望输出。它特别适合于求解内部机制复杂的问题。我们无需建立模型，或了解其内部过程，只需输入合理的数据就可以获得输出。理论上，一个三层的神经网络，能够以任意精度逼近给定的函数，这是非常理想的期望。

1 计算方法

MATLAB是美国Mathworks公司推出的一套高性能的数值计算和可视化软件，尤其是软件中包括了许多专业性较强的工具箱，可以通过修改其内置的源程序来构成新的工具箱，从而避免了复杂的子程序编程任务。

在进行BP神经网络设计时，一般应从网络的层数，每层中包含的神经元个数和适当的激活函数、以及学习速率等几个方面来进行考虑。

理论上已经证明:具有偏差和至少一个S型隐含层加上一个线性输入层的网络，能够逼近任何有理函数。增加层数的优点是可以进一步的降低计算误差，提高精度，但同时会使网络复杂化。要使网络训练精度提高，可以采用一个隐含层，增加网络包含的神经元数的方法来获得，这在结构实现上，要比增加数量更多的隐含层要简单的多。本文中的BP神经网络采用三层结构:输入层节点数为3，隐含层节点数为8，输出层节点数为1。

传递函数又称激活函数，是BP神经网络的重要组成部分，它必须是连续可微调的，BP神经网络常采用 S型的对数或正切函数和线性函数。在本文中，输入层到隐含层的激活函数选用tansig正切函数，隐含层到输出层的激活函数选用pureline线性函数。

学习速率决定每一次循环训练中所产生的权值变化量。大的学习速率可能会导致系统的不稳定;但小的学习速率将导致较长的训练时间，造成收敛很慢，不过能保证网络的误差值不超出误差表面的低谷而最终趋于误差最小值。所以一般情况下，通常倾向于选取较小的学习速率以保证系统的稳定性。学习速率的选取范围基本在0.01～0.8之间。本文中的学习速率取0.01。

MATLAB中有几种典型BP神经网络算法，以下分别将其进行计算比较:

(1)trainrp弹性BP算法。它只用导数的符号表示权更新的方向，而不用考虑导数的大小。因此可以消除偏导数大小对权值的不利影响。这种算法具有收敛速度快，且占用内存小的优点。

(2)traingdx自适应学习速率法。用它检查权重的修正值是否真正降低了误差函数。如果确实如此，则证明选取的学习速率有上升空间，可以加大学习速率的值。如果不是，那么就要减小学习速率的值。因此速率大小可以根据误差性能函数来调节，能够解决一般BP算法中学习速率大小选择不当的问题。

(3)traincgf共轭梯度法。这是采用Fletcher-Reeves算法的共轭梯度算法。这种算法的收敛速度比普通的梯度下降法要快很多。这种方法需要通过线性搜索，存储量的要求很大，对收敛速度来说，不同的对象会不同。这种算法的计算代价比较低，在解决较大规模问题中十分有用。

(4)trainbfg拟牛顿算法。它的权值根据X=X+a*dX来修改，dX表示搜索的方向，a为沿着搜索方向来最小化性能函数。最初的搜索方向将沿着梯度的负方向，再之后的迭代中按dX=－H－1*gX来修改，H为近似Hessian矩阵。这种算法需要的迭代次数比较少，但由于需要每步都要存储Hessian矩阵，所以每一步计算量和存储量都很大，适用于小型网络。

(5)trainlm:Levenberg-Marquardt优化算法。权值根据dX=－(jXT*jX+i*mu)－1jXT*E进行修正，其中jX为误差对权值微分的Jacobian矩阵，E为误差向量，mu为调整量。这种算法学习速度很快，但占用内存较大，对于中等规模的网络来说，是最好的一种训练算法。对于大型网络，可以通过设置参数mem-reduc，将Jacobian矩阵分解为几个子矩阵。这样可以大大减少内存的占用，但学习时间会增大。

2 计算结果

本文的样本数据来源于某钢厂1450六辊轧机的120组轧制力数据，预先对原始数据进行处理，使输入层只包括对轧制力影响最大的要素，包括轧前厚度，轧后厚度，变形抗力，输出层为单位宽度轧制力。通过对样本数据的学习来对样本以外的实测数据进行预报，验证不同算法的网络泛化能力，五种算法的计算结果见表1。

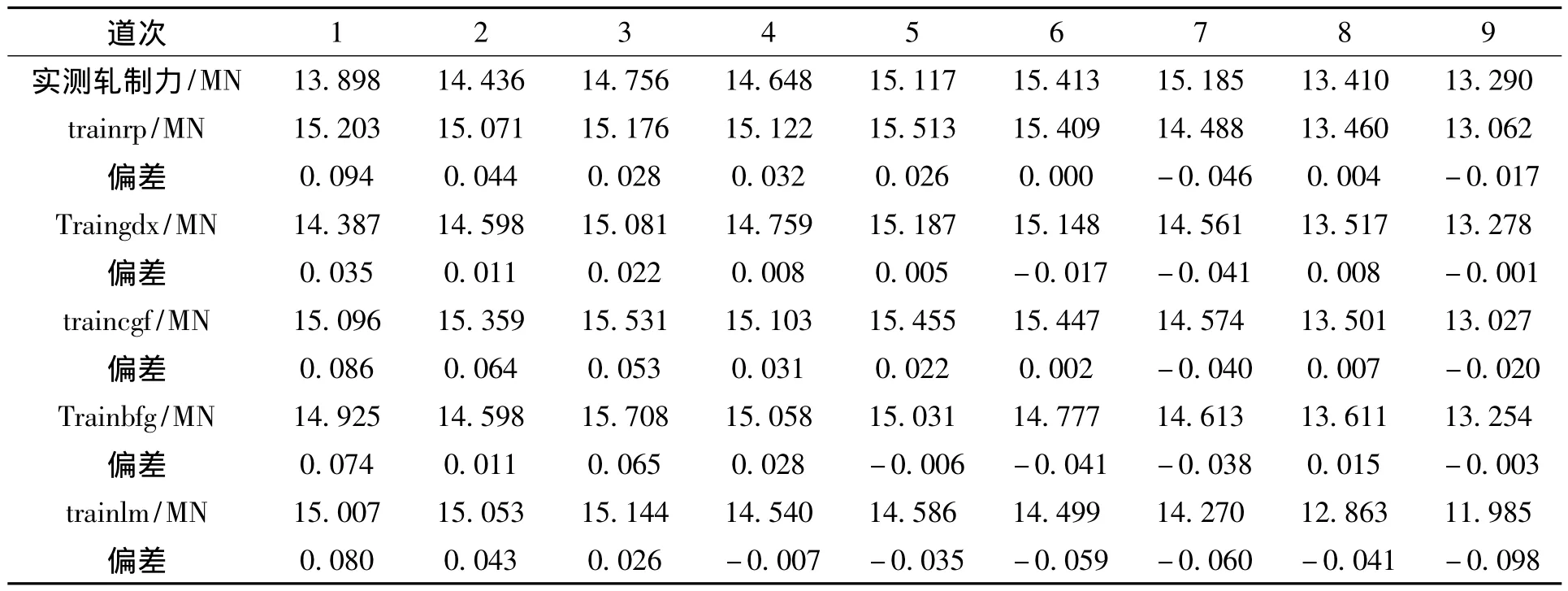
表1 五种算法的计算结果Tab.1 Calculation results of five algorithms

从表1可以看出，五种算法的偏差分别为:traingrp算法最大偏差0.094，平均偏差0.032;traingdx算法最大偏差0.041，平均偏差0.016;traincgf算法最大偏差0.086，平均偏差0.036;trainbfg算法最大偏差0.074，平均偏差0.031;traingdx算法最大偏差0.098，平均偏差0.050。

3 结论

将 BP神经网络中的 traingrp、traingdx、traincgf、trainbfg、traingdx五种典型算法应用于本文实例，五种算法中traingdx算法的误差最小，在9个道次中的最大偏差为0.041，平均偏差为0.016，属最佳算法，应用于轧制力计算可以取得良好的效果。

［1］闻新，周露，王丹力，等.MATLAB神经网络应用设计［M］.北京:科学出版社，2001.

［2］飞思科技产品研发中心.神经网络理论与MATLAB7实现［M］.北京:电子工业出版社，2005.