标准表法流量标准装置检定中标准流量计的不确定度探讨

曹久莹

(江苏省计量科学研究院，南京 210007)

0 引言

依据JJG 643—2003《标准表法流量标准装置》检定规程，对于非定点使用的标准流量计，使用仪表系数时，其测量A类标准不确定度的计算方法为：

式中：eK为用最小二乘法拟合的流量-仪表系数曲线的标准不确定度，1/m3；K为标准流量计的常用仪表系数，1/m3。

由于规程中并没有详细说明最小二乘法拟合流量-仪表系数曲线的计算过程，下面主要探讨一下如何使用最小二乘法进行曲线拟合及曲线标准不确定度的确定。

1 最小二乘法

1.1 最小二乘法的基本原理

在物理实验中经常要观测两个有函数关系的物理量x和y。根据两个量的多组观测数据来确定它们的函数曲线，这就是实验数据处理中的曲线拟合问题。这类问题通常有两种情况：一种是两个观测量x与y之间的函数形式已知，但一些参数未知，需要确定未知参数的最佳估计值；另一种是x与y之间的函数形式也未知，需要找出它们之间的经验公式。后一种情况通常假设x与y之间的关系是一个待定的多项式，多项式系数就是待定的未知参数，从而可采用类似于前一种情况的处理方法。

本文讨论的标准流量计的流量-仪表系数这两个量的函数曲线即属于后一种情况，由于流量计种类繁多，检定时并不能准确知道该流量计的流量-仪表系数之间的函数关系，往往只能得到一组或多组检测数据，为了确定其函数关系，就需先假设一个多项式，再通过解数学方程的方法求解该多项式的参数。

设x和y的函数关系为以下理论公式：

y=f(x；a1，a2，……am)

式中：a1，a2，……am是m个要通过实验确定的参数。设有n组观测数据，对于每组观测数据(xi，yi)(i=1,2,……n)都对应于xy平面上一个点。若不存在测量误差，则这些数据点都准确落在理论曲线上。只要选取n组测量值代入上式，便得到方程组：

yi=f(xi；a1，a2，……am)

式中：i=1,2,……n。求n个方程的联立解即得n个参数的数值。显然，当nm的情况下，上式成为矛盾方程组，不能直接用解方程的方法求得m个参数值，只能用曲线拟合的方法来处理。

曲线拟合的具体作法是：对给定数据(xi，yi)(i=1,2,……n)，确定近似函数y=f(x),使误差ri=f(xi)-yi(i=1,2,……n)的平方和最小，即：

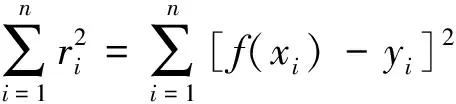
从几何意义上讲，就是寻求与给定点(xi，yi)(i=1,2,……n)的距离平方和为最小的曲线y=f(x)。函数f(x)称为拟合函数或最小二乘解，求拟合函数f(x)的方法称为曲线拟合的最小二乘法。

1.2 多项式拟合

在曲线拟合中，拟合函数可以有不同的选取方法。

当拟合函数为多项式时，称为多项式拟合，满足上式的fm(x)称为最小二乘拟合多项式。当m=1时，称为线性拟合或直线拟合。

多项式拟合一般可归纳为以下几个步骤：

1)确定拟合多项式的次数m；

2)写出正规方程组，求出系数a0，a1，……am；

在多项式拟合中，当拟合多项式的次数较高时，其正规方程组往往是病态的，而且：

1)正规方程组系数矩阵的阶数越高，病态越严重；

2)拟合节点分布的区间[x0,xm]偏离原点越远，病态越严重；

3)xi(i=1,2,……n)的数量级相差越大，病态越严重。

为了克服以上缺点，一般采用以下措施：

1)尽量少作高次拟合多项式，而作不同的分段低次拟合；

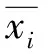
下面讨论几种常用的表示两个观测量函数关系的多项式，来进行曲线拟合的计算方法。

1.2.1 直线拟合

曲线拟合中最基本和最常用的是直线拟合。设流量q和仪表系数k之间的函数关系为如下的直线方程：

k=a+bq

(1)

式中有两个待定参数，a代表截距，b代表斜率。解方程组可求得直线参数a和b的最佳估计值：

(2)

(3)

相关系数：

(4)

式中：Qi为实际检测得到的流量值(m3/h)，i=1，2，…n，n为实际检测次数；Ki为实际检测得到的与流量值对应的仪表系数(1/m3)，i=1，2，……n，n为实际检测次数。

说明：1)可用数学软件计算出参数a、b、r的值；2)可用Excel中的函数intercept、slope和correl命令直接求得参数a、b、r的值。

1.2.2 曲线拟合

按照上述多项式拟合的方法，避免当多项式的次数较高时其正规方程组出现病态，本文选取次数不超过3次的多项式，按以下几种函数关系式进行流量q和仪表系数k的曲线拟合：

数学模型1：k=a+bq+cq2

(5)

数学模型2：k=a/q+b+cq

(6)

数学模型3：k=a/q2+b/q+c+dq+eq2

(7)

数学模型4：k=a/q3+b/q2+c/q+d+eq+fq2+gq3

(8)

其中，a、b、c、d、e、f、g均为拟合曲线的参数。

采取人工解方程组的方法来计算上述方程中的参数，工作量大且不易操作，目前较简便的方法可通过计算机数学软件MATLAB编制特定的程序来求得各个参数值。

2 举例说明

以一台G650双腰轮标准流量计的检测结果数据为例，10个流量点下的仪表系数见表1。

表1 流量计流量点和仪表系数的检测结果数据

下面按照本文中列举的5种函数关系式，分别进行多项式拟合，并求出各拟合曲线的标准不确定度。

2.1 直线拟合

将表1中检测数据带入式(2)、(3)、(4)可以得出直线拟合的各个系数的值为：

a=2022.2865，b=0.0211，r=0.9664

根据所求得的相关系数r值，可看出a和b成线性关系，将a和b的值代入式(1)，得拟合直线为：

k=a+bq=2022.2865+0.0211q

分别计算每个流量点下的ki：

ki=a+bQi

其中，ki为将实际检测流量值Qi代入拟合直线公式中得到的拟合仪表系数，为计算过程中间量。

计算拟合曲线的标准偏差eK：

其中，i=1，2，……n，n为实际检测次数。

中间计算数据一览表见表2。

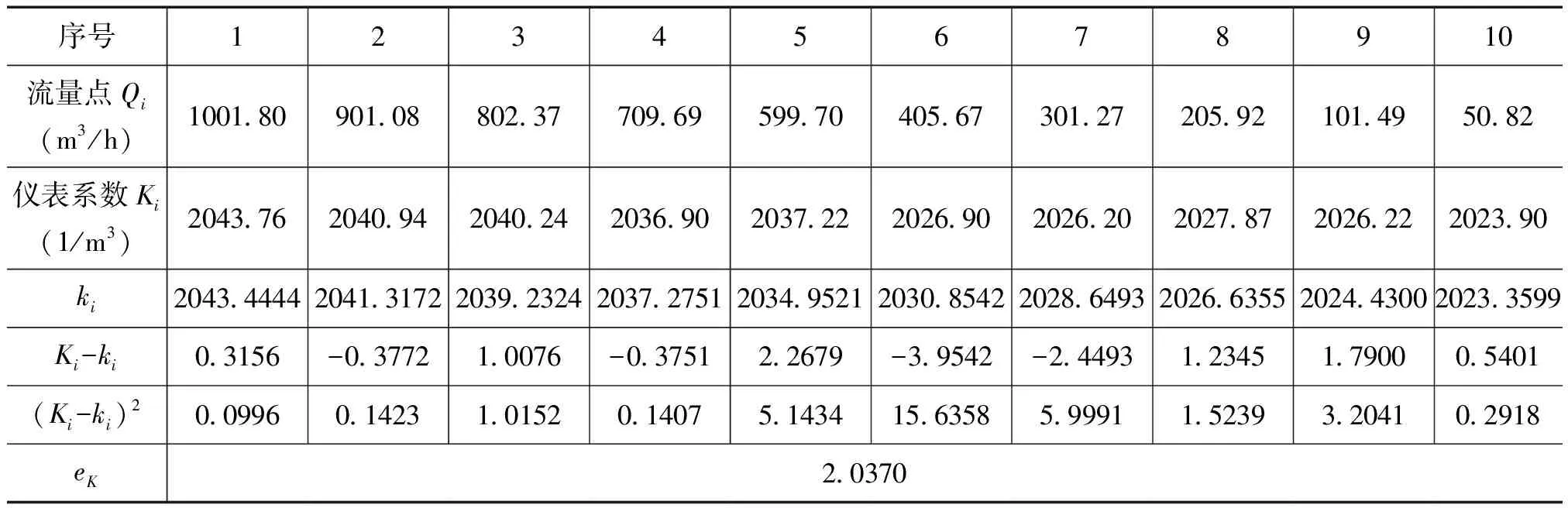
表2 直线拟合的标准偏差及中间运算数据

标准流量计的测量A类标准不确定度uh：

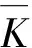
2.2 曲线拟合

按照式(5)、(6)、(7)、(8)所列的4种函数关系式分别进行流量q和仪表系数k的曲线拟合。这里使用数学软件MATLAB编程求出a～g各个系数的值，分别代入式(5)、(6)、(7)、(8)得到各函数关系式分别表示如下：

k=a+bq+cq2=2023.5251073+0.01315295q+

0.00000773q2

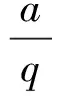
2020.599975+0.02306549q

k=a/q2+b/q+c+dq+eq2=

-88208.41949294/q2+2547.93984259/q+

2005.21202409+0.05244346q-

0.00001653q2

k=a/q3+b/q2+c/q+d+eq+fq2+gq3=

131270373.972628/q3-5042607.141/q2+

62933.34847/q+1702.05387+

0.74070827q-0.00071686q2+

0.00000026q3

按2.1的步骤计算出每个流量点下的ki和曲线的标准偏差eK，并计算出标准流量计的测量A类标准不确定度uh，数据一览表见表3。

表3 曲线拟合的标准偏差和中间运算数据

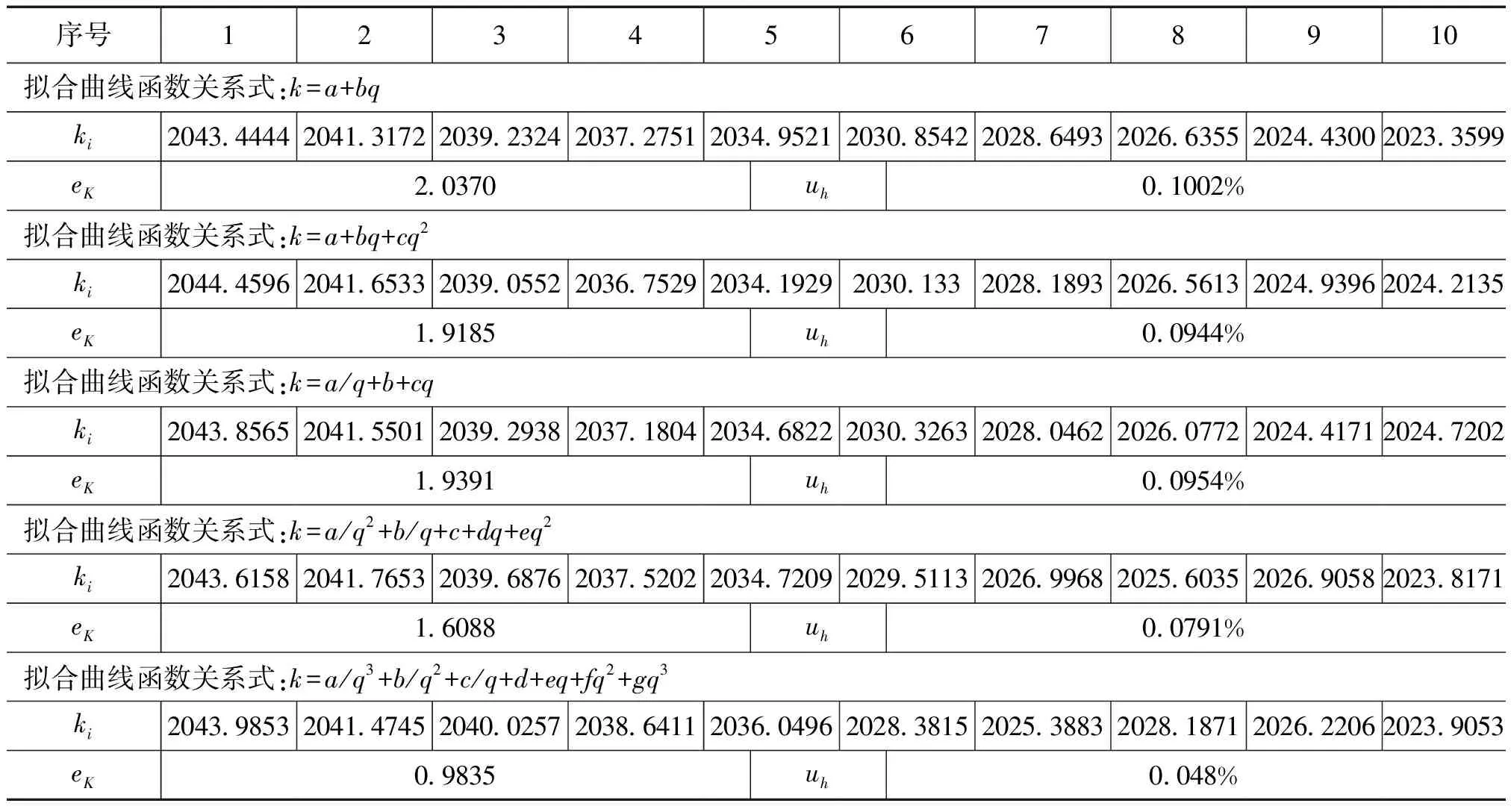
续表

流量-仪表系数的检测数据曲线图和拟合曲线图分别见图1和图2。

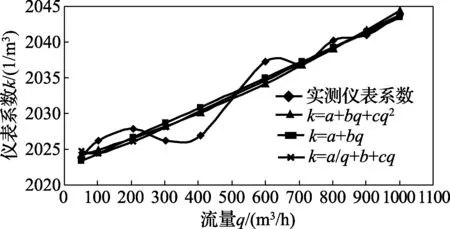
图1 流量-仪表系数的检测数据曲线和拟合曲线对比图(1)

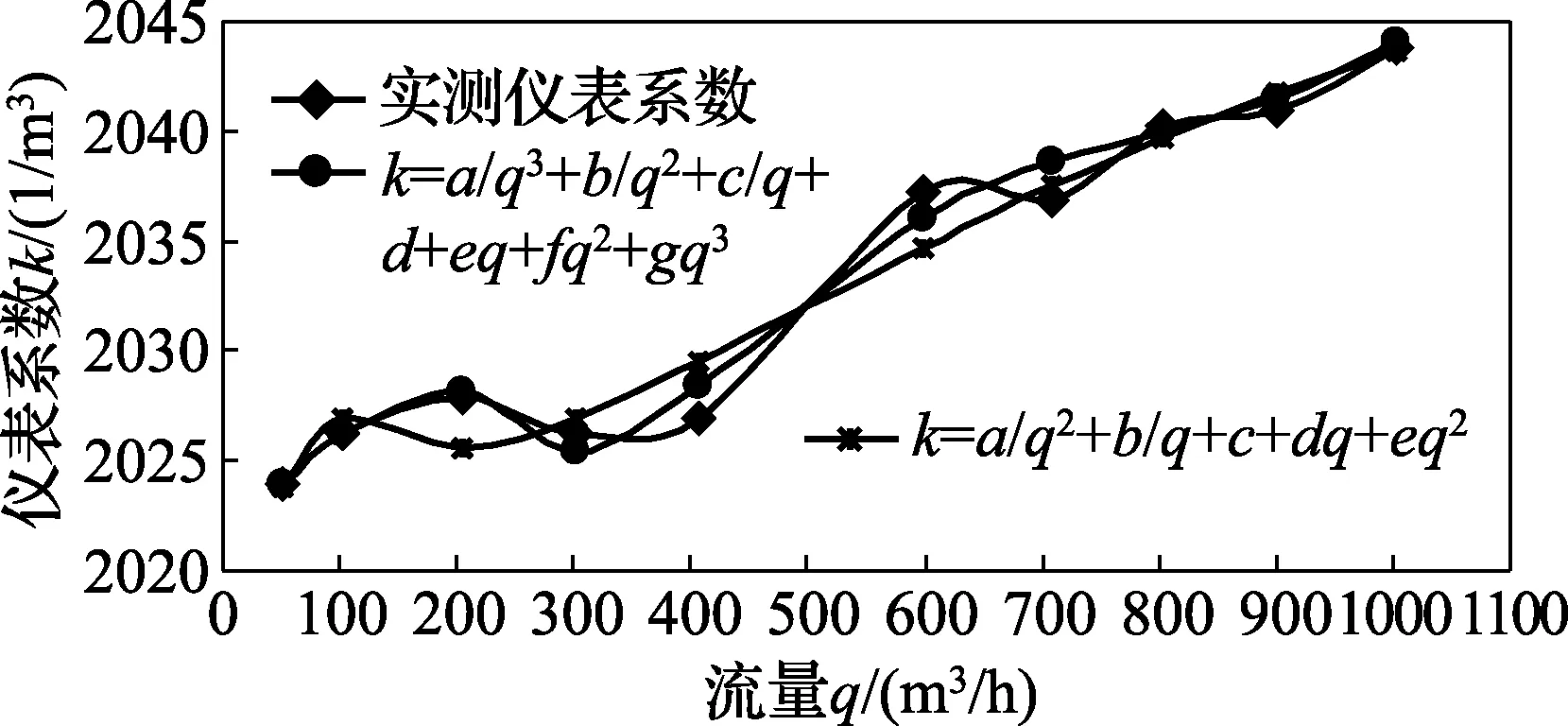
图2 流量-仪表系数的检测数据曲线和拟合曲线对比图(2)

3 结束语

按照最小二乘法对流量-仪表系数进行曲线拟合可以有多种函数表达方法，从以上的计算数据和流量-仪表系数曲线图可以看出，直线拟合使用起来最简单，计算过程容易实现，但拟合曲线的不确定度较大；而曲线拟合根据所使用数学模型的次数不同有多种不同的函数表达式。本文中列举的数据计算结果虽然随着次数增加，拟合曲线与实际测量值的曲线越接近，拟合效果越好，拟合曲线的不确定度越小，但随着次数越高公式越复杂，计算过程难度越高，人工计算参数有一定难度，需通过计算机软件辅助实现其计算过程，而且次数越高，拟合曲线也可能会有实际并不存在的凹陷和突起，其实际应用效果不一定很好。因此，目前通常使用较多的是不超过3次的曲线拟合，如直线拟合和对称低次曲线拟合方法。实际工作中可以根据情况需要和检测数据选取合适的曲线拟合函数来进行不确定度的计算。

参考文献

[1] JJG 643—2003标准表法流量标准装置检定规程.中国计量出版社，2003

[2] 段慧明，史振东.标准流量计的计量性能评定.计量技术，2008(9)

[3] 刘庆，邵志新.回归分析的直线拟合不确定度探讨.中国测试，2009(5)

[4] 同济大学数学系.高等数学(下册).第6版.高等教育出版社，2007

[5] 李庆扬，王能超，易大义.数值分析.第5版.清华大学出版社，2008