一种快速的三维点云自动配准方法

谢冬香，刘先勇

(西南科技大学 信息工程学院，四川 绵阳 621000)

在机器视觉众多应用领域中,如立体匹配、图像配准和形状识别等，点云配准操作一直都是一个关键步骤。点云配准就是将一片点云(测试点集)的坐标匹配到另一片点云（参考点集）的坐标下，从而达到两片点云坐标的一致性，其配准精度直接影响后续误差分析的可靠性。目前，常用的配准方法有遗传算法、最小二乘匹配方法、三点对齐法以及ICP算法。遗传算法和最小二乘匹配方法需要多次迭代处理，计算复杂度高并且配准时间长；三点对齐法实现原理简单，能够很快地实现初始配准，但必须准确地确定出3对基准点的对应关系[1];ICP算法是一种众所周知的算法[2],传统的ICP算法虽简单，但在实际应用中具有限制性，因为它假设每一个点都可以在对应的点集中找到对应点，当两模型数据不一样时，该假设就不成立。

在配准过程中,涉及旋转和平移矩阵的求取，EGGERT D W等人对比了奇异值分解法(SVD)、正交矩阵法(OM),单四元素法(UQ)以及双四元素法(DQ)4种当前流行和最有效算法的鲁棒性和精确度[3],运用分离算法测试了4种算法的稳定性。在非退化数据点集的情况下,大多数情况SVD和UQ是相似的,少量情况下是SVD更好一点,OM对于平面数据点集不稳定,而DQ算法则没有一种情况比其他3种算法好。基于这些测试结果，本文采用SVD来得到旋转矩阵。

1 本文算法

主成分分析方法(PCA)的基本思想是,采用统计方法,对多变量表示数据点集合寻找尽可能少的正交矢量表征数据信息特征。本文采用PCA定义了简单的数学模型和轴向确定方法等。本文配准算法简单、稳定可靠、计算速度快且计算复杂度小。

1.1 数学公式定义

定义1三维数字图像的绕矩定义为：

绕矩mijk的次数定义为i+j+k。

定义2设三维数字图像的质心为(gx,gy,gz),则中心绕矩为：

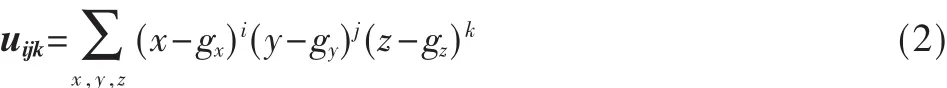
定义3设数字图像的惯量矩阵I定义为：

其中，Ixx=u200,Iyy=u020,Izz=u002，Ixy=Iyx=u110，Ixz=Izx=u101，Iyz=Izy=u011。

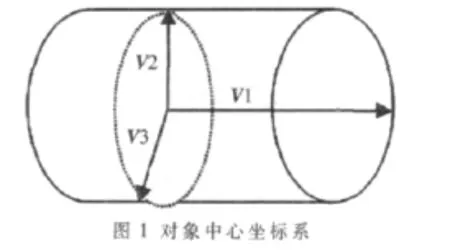
定义4由于惯量矩阵I是对称的，因此一定存在实特征值。 设 λ1、λ2、λ3是惯量矩阵的 3个实特征值,这 3个实特征值一定有3个不同的特征向量，正交化后一定存在一组对应的正交特征向量 V1、V2和 V3，将这 3个特征向量称为物体的一组主轴。将物体的质心作为坐标原点并将其与这一组主轴一起定义为对象中心坐标系,如图1所示。

1.2 算法流程

本文算法主要是通过计算测试点集到参考点集的平移和旋转矩阵将测试点集配准到参考点集下，图2为算法的流程图。

图2 算法流程图

1.3 旋转平移矩阵的获取

计算参考点集和测试点集的质心。为了提高算法的速度，本文采用以下质心计算方法：

其中,n代表点集的个数。根据定义2、定义 3计算惯量矩阵 I，由定义 4可以得到参考点集和测试点集的惯量矩阵 I1、I2的特征值和特征向量。以 I1为例，得到正交特征向量 V1、V2和V3,以这3个特征向量建立坐标系有8种情况，首先规定坐标系必须满足右手规则，便可去掉4种情况。2008年张树森采用包围盒到去掉配准方向相反的情况,该方法计算速度非常慢[4]。本文先找到最大特征值对应的正交特征向量V1，然后寻找点集中离质心最远的点，如果此点与特征向量V1的夹角小于 90°，则u1=V1,反 之，u1=-V1， 同 理 可 以 求 得 u2，u3=u1×u2， 大 大 提高了配准速度。

得到了参考点集和测试点集的正交特征向量后，旋转平移变换就转换为求取两组正交向量组的变换。由此可以得到待SVD分解的两点集相关矩阵为[5]：

其中,Dci、Mci分别是参考点集和测试点集的正交特征向量组成的向量矩阵。设H的奇异值分解为H=USVT，因此旋转矩阵R的最优解为：

最优的平移矩阵就是将测试点集的中心移动到参考点集的中心下。设测试点集和参考点集的中心分别为T0和C0，则可以得到平移矩阵T为：

最后得到旋转平移矩阵M：

其中，R 为 3×3的矩阵，0为 3×1的矩阵，T为 1×3的矩阵。将所有测试点集乘以此旋转平移矩阵并将其移动到参考点集下，实现了快速配准。

2 测试效果

以下所有测试实验均是在CPU为2.52GHz,内存为3.50 GB的环境下进行的,采用了C++语言和OpenCV 2.3.1基础库，并在VS 2008软件平台上编译运行。为了验证算法的稳定性，测试选用了不同的形状，图3所示为3种典型模型的配准效果。其中，模型1为绵阳铁牛科技扫描的点云,模型2和模型3的点云采用的是Geo-magic Qualify 12中的模型。从图3可以看到，这3种模型都可以实现配准。

表1为各种模型的两片配准模型的点云个数和粗配准所需要的时间，可以看出，点云数据在几十万的情况下，配准时间全都是ms级。

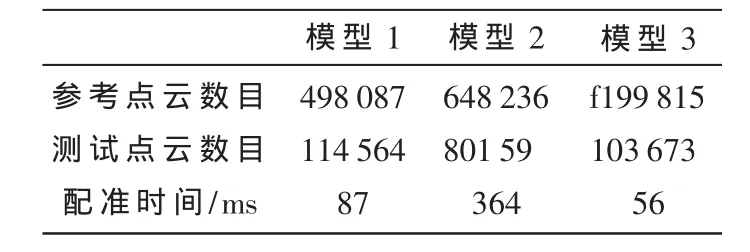
表1 配准点云数目和配准所需要的时间

实验结果证明,本文采用的配准方法算法简单、稳定可靠、计算速度快且计算复杂度小，对实现大量点云快速配准具有使用价值。

[1]严平，孙肖霞.基于CAD模型的涡轮叶片误差检测系统[J].北京航空航天大学学报,2008,34(10):1159-1162.

[2]BESL P J，MCKAY N D.A method for registration of 3-D shapes[J].IEEE Transactions on Pattern Analysis andMachine Intelligence(S0162-8828),1992，2(14):239-256.

[3]EGGERT D W,LORUSSO A,FISHER R B.Estimating 3-D rigid body transformations:a comparison of four major algorithms[J].Machine Vision and Applications(S0932-8092),1997,9:272-290.

[4]张树森，李玮,程俊廷.基于逆向工程的三维测量点云数据与CAD数模配准算法研究[J].制造技术与机床，2008(3);114-117.

[5]APLPERT M,BRADSHAW J G.The principal axes transformation-a method for image registration[J].The Journal of Nuclear Medicine(S0161-5505),1990(31):1717-1722.