一种新型并串联稳定平台系统研究

王洪瑞，王立玲，肖金壮，刘秀玲，高 征

(河北大学 电子信息工程学院，保定 071002)

0 引言

稳定平台广泛应用于机载、舰载、车载武器等军事领域和空间遥感探测、公安消防、环境监测等民用领域。为了实现运动载体设备的稳定以保证对目标的精确跟踪，稳定平台集惯性导航、微惯性传感器、数据采集及信号处理、精密机械建模仿真和设计、电机运动控制、图像处理和光学仪器应用等多项技术于一身[1]。现有的这些稳定平台基本上都是串联结构，由于其结构特点是本体过重和驱动力小，使得其在大负载场合的应用存在难于控制的问题。因此，承载大，具有大工作空间和高动态响应的并联稳定平台成为热点问题。但是，由于少自由度并联机器人机构运动学、动力学分析的复杂性和理论研究的滞后，限制了采用这类机构作为新型的稳定平台机构的发展。对球面并联机构的研究大多集中在球面3自由度并联机器人机构上[2,3]，球面二自由度机器人特别适用于空间姿态变化的地方。纯粹软件仿真很难真正模拟实际机构的特性[4]。

本论文研制一套新型稳定平台装置，根据稳定平台工作原理和物理特性设计平台伺服控制系统，对稳定平台系统进行深入的研究。根据稳定平台运动学关系和驱动装置的动态模型，以增量式光电编码器作为位置反馈和倾角传感器作为目标偏差检测、以光纤陀螺（FOG）作为惯性速率敏感元件，建立基于计算力矩的稳定平台伺服控制系统。通过在Matlab中嵌入QuaRC实时控制软件编程实现半实物仿真。

1 系统构成

1.1 硬件

机构简图如图1所示。

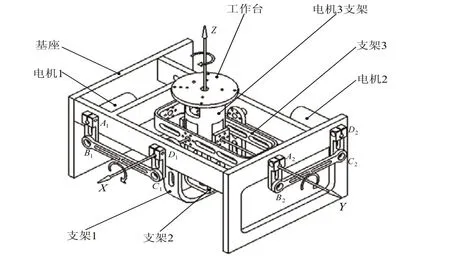
图1 3-DOF稳定平台机构

图1中，支架1与支架2轴线垂直交于一点，电机1和电机2安装于底座上，并通过平行四边形A1B1C1D1和A2B2C3D2分别驱动支架1和支架2，构成二自由度球面并联机构。引入平行四边形结构可改变电机的安装位置，改善机构整体的紧凑性。支架3长度较大，保证操作台有更大的俯仰范围。电机3安装于支架2内，构成串联结构，顶端安装工作台，可以360度旋转。选用NI PCI-6230控制卡。Advantech IPC进行数据采集、处理、与控制算法运行，该板卡为Quanser实时软件产品所兼容，可以利用Matlab中丰富的软件资源。

1.2 软件

在稳定平台进行半实物仿真时，为了给高速、高精度控制算法研究提供一个理想平台，本研究中采用了在Matlab软件中嵌入QuaRC的方式实现，这样可在Simulink中可方便调用Matlab中丰富的软件模块或算法。并通过QuaRC提供的编译环境，对Simulink程序进行编译[5]，生成可实时运行的控制程序。可以直接访问NI PCI-6230多功能通用控制卡，减少系统控制器的开发周期。

1.3 控制系统设计

1.3.1 系统模型

1）3-DOF稳定平台机构

根据3-DOF稳定平台机构工作原理，以刚体空间运动学为基础, 借助欧拉角法与向量法[5,6]建立该机构执行电机输入转角和工作台输出横滚角、俯仰角和方位角之间关系如下。

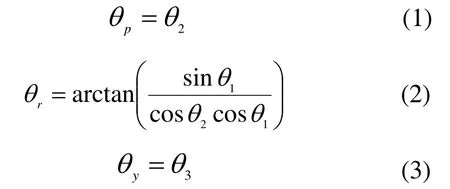
其中，321,,θθθ为电机1、电机2和电机3的输入转角，yrpθθθ,,稳定平台输出的俯仰角、滚转角和方位角。稳定平台雅可比矩阵：

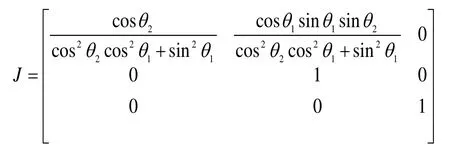
2）驱动装置的动态数学模型

本系统驱动采用伺服电机，只存在电磁转矩直接耦合，伺服电机动态电压方程为：

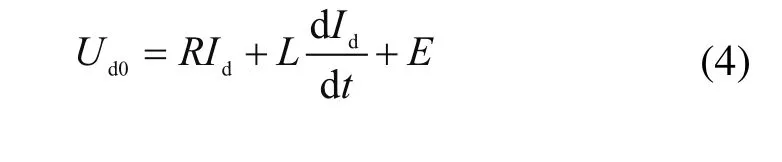
其中，Udo电机电压，R电枢回路总电阻，L电枢回路总电感，Id电枢中电流，E额定励磁下的感应电动势。

如果，忽略粘性磨擦及弹性转矩，电机轴上的动力学方程为：

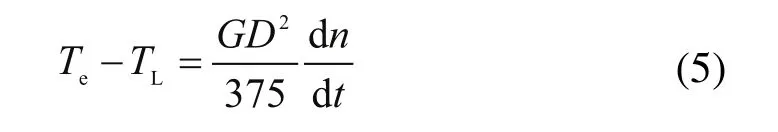
额定励磁下的感应电动势和电磁转矩分别为：

在零初始条件下，得电机的动态数学模型如下：

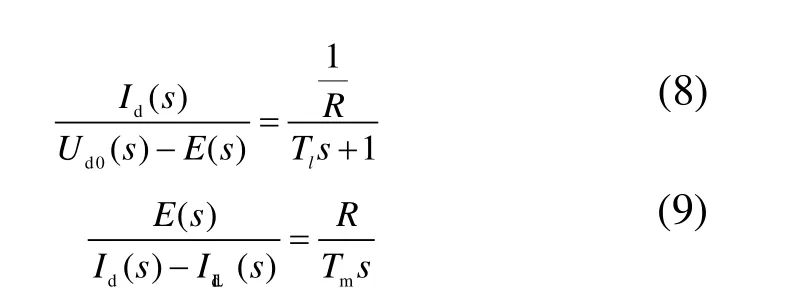
把传动部分和支架的转动惯量折算到电动机转子上，得到用于控制的电磁转矩直接耦合机电系统动力学方程为：

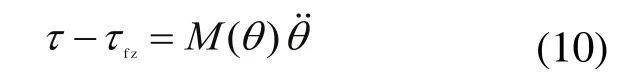
其中τ电动机输出电磁转矩，τf z电动机传动轴的等效负载转矩（摩擦转矩），M(θ)为电机转子、传动部分和支架折算到电机轴上的总转动惯量。θ为电动机转轴的转角。通过（1）、（2）和（3）式导出系统被控量θp,θr,θy。

1.3.2 控制方案

对于3-DOF稳定平台机电系统，由于有很多干扰影响控制系统的运动，因此计算力矩动态控制的方法[7]实现系统的角位置和角速率控制是合适的，如下设计控制器：

(11)代入到（10）有系统误差方程为：

2 系统半实物仿真实验

2.1 系统模型参数

其他参数如表1所示。

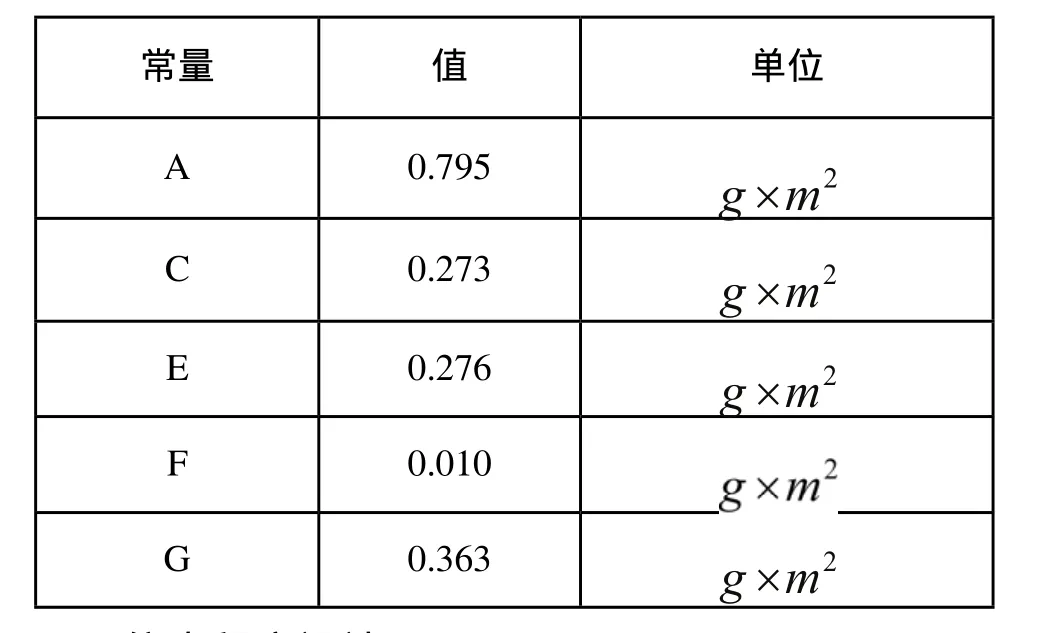
表1 系统模型参数表

2.2 仿真程序设计

在进行半实物仿真时，控制程序和指令通过在PC机编程实现，编程软件是在Simulink中搭建仿真程序，如图2所示。

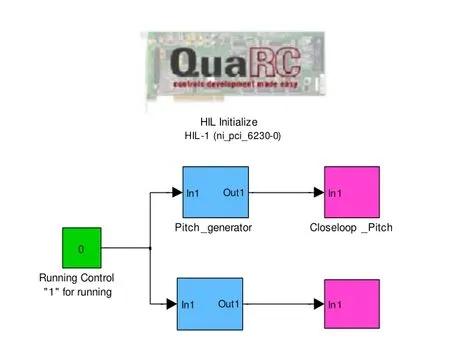
图2 Simulink控制程序

图2中，HIL Initialize模块完成对控制卡PCI 6230的初始化。Pitch_generator中采集基座俯仰角，并转化为球面机构俯仰角补偿量，Closeloop_Pitch通过对电机2进行位置控制[6]，实现对基座俯仰分量的补偿，保持其在俯仰方向分量的水平。基座横滚角分量的运动补偿通过Roll_generator模块和Closeloop_Roll实现。

根据（15）式取:

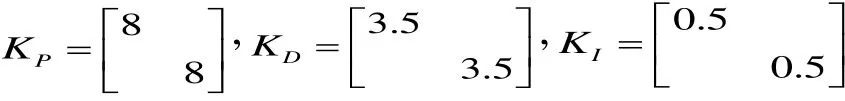
2.3 实验结果

通过锁定其它轴系，分别对其施加周期为10s，幅值为rad5.0±俯仰激励、横滚激励，验证3-DOF稳定系统构建的有效性。将两轴对角度的跟踪曲线进行绘制，如图3、图4所示。

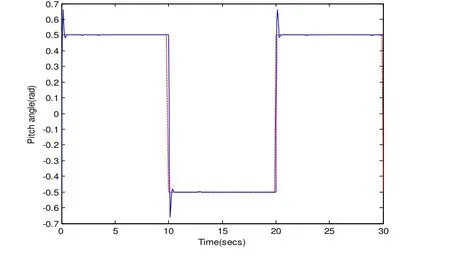
图3 俯仰轴跟踪曲线

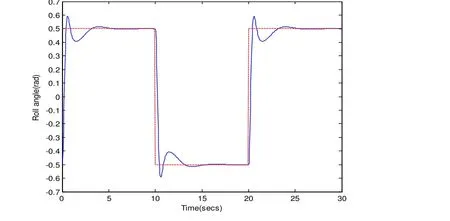
图4 横滚轴跟踪曲线

图4、5中，实线分别为横滚和俯仰角跟踪曲线， 从图中可看出，在±0.5rad的运动范围内，对俯仰轴，1秒之后进入稳定状态，横滚轴2秒后进入稳态，横滚超调比较小。

3 结论

所设计研制的3-DOF并串联稳定平台能够在实验室条件下模拟车载光电成像跟踪系统等运动学特性和空间运行姿态。基于开放式结构、标准模块化控制器的稳定平台伺服系统的建立，为光电稳定跟踪系统相关技术的研究和验证提供了一个有效的、与实际系统比较相似的模拟环境，为进一步研究宽频带、高性能的此类伺服系统的精度提供了良好的平台，可为实际系统的研制和改进提供参考依据和实验数据。

[1] 杨蒲,李奇.三轴陀螺稳定平台控制系统设计与实现[J],中国惯性技术学报,2007,15(2):171-176.

[2] 王惠君,王惠飞,车载三轴稳定平台的陀螺耦合分析[J]，制造业自动化,2011,33(3):106-108.

[3] 沈晓洋,陈洪亮,刘昇.机载陀螺稳定平台控制算法[J],电光与控制,2011,18(4):46-50.

[4] J.M. Hilkert. Inertially Stabilized Platform Technology[J],IEEE Control Systems Magzine,2008,2:26-46.

[5] Toshiaki Tsuji,Takuya Hashimoto,Hiroshi Kobayashi.A Wide-Range Velocity Measurement Method for Motion Control[J].IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS,2009,56(2):510-519.

[6] Alon Wolf,Moshe Shoham,Screw theory tools for the synthesis of the geometry of a parallel robot for a given instantaneous task, Mechanism and Machine Theory.2006,41(5):656-670.

[7] Prasatporn Wongkamchang,Viboon Sangveraphunsiri.Control of Inertial Stabilization System Using Robust Inverse Dynamics Control and Adaptive Control[J],2008,13(2):20-32.