结合Bresenham直线算法的运动模糊方向判断方法

梁 菁

（梧州学院 计算机科学系，梧州 543002）

0 引言

在拍摄时成像设备和被拍摄景物之间发生相对运动而造成图像模糊称为运动模糊。在我们国家，许多城市的道路上都安装有“天眼”设备，高速公路的收费站也设有摄像头，这些摄像设备能够拍摄下所有经过车辆包括车牌号码、车型等信息的图像。但图像形成时由于车辆大多数处于运动的状态而产生了模糊的现象，这就是运动模糊。图像模糊给识别车辆信息造成了麻烦，所以我们要利用一些方法对图像进行恢复，以获取需要的信息。

在图像的拍摄形成、存储、传输和输出显示过程中，受到噪声或相对运动的影响，会发生不同程度的变质、失真和退化。根据模糊图像提供的信息，运用某些先验知识，建立数学模型，从而将退化图像以最大的保真度恢复原来的图像，便是图像恢复的目标和任务[1]。

目前已经有许多运动模糊图像复原的算法，如维纳滤波法、L-R算法，但这些算法都要求有足够的退化知识，知道点扩散函数才能对模糊图像进行恢复。对于实际拍摄所得的模糊图像，在恢复之前就必须先求出相应的点扩散函数PSF(Point Spread Function)[2]，才能用上述的恢复算法进行图像复原。

匀速直线运动模糊图像的点扩散函数由模糊运动的方向与运动长度来确定，所以求出图像运动的方向以及运动了多长的距离是恢复过程中重要的步骤。

一些学者[3]提出了应用倒频谱分析法估算PSF参数的方法，但这种方法在模糊长度范围为5至55像素时估算误差较小，当模糊长度超过这个范围时，误差值会急剧增加。有研究人员[4]提出对模糊图像进行两次傅立叶变换，对处理后的图像利用灰度统计方法检测倾斜角以判断运动方向的方法，但没有给出实现的具体算法。而且在文献给出的两次傅立叶变换后的图像中，所提及的这种计算方法核心的部分—亮线并不明显，给图像灰度统计带来不少难度。

本文提出一种结合计算机图形学中Bresenham算法对图像的频谱图进行灰度求和进而确定运动模糊方向的算法。

1 运动模糊的原理及分析

数字图像在计算机上是以位图的形式存在的，位图是一个矩形点阵，矩形点阵中每个元素称为像素，它是数字图像中的基本单位。一幅M×N大小的图像，是由M×N个明暗不等的像素组成。在数字图像中各个象素的明暗程度是由灰度值来表示的。若将白色的灰度值定义为255，黑色的灰度值定义为0，则由黑到白的明暗度可以均匀地划分为256个等级，每个等级表示一种唯一的灰度。

图像的运动模糊是在成像设备快门开启至关闭这一曝光过程中被摄物和成像系统相对运动造成的。我们以匀速直线运动模糊为例来进行讨论。因为匀速直线运动模糊图像具有一般性和代表性，变速的、非直线的运动在成像瞬间可以视为匀速直线运动。

所以从物理现象上看，运动模糊图像实际上就是同一景物图像经过一系列距离延迟后再叠加，最终形成的图像。而我们所处理的数字图像由若干个像素来构成，所以图像运动实际上是组成这幅图像的所有像素进行移动。

一幅图像可以定义为一个二维函数f(x,y),其中x和y是空间坐标，而f在任意一对(x,y)处的幅度称为该点处图像的灰度或亮度。在线性平移空间不变运动模糊系统中，用f(x,y)表示输入的原始图像，g(x,y)表示输出的模糊图像，则两者的关系可以用下面的方程来表示：

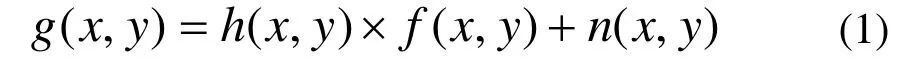
其中h(x,y)为退化函数的空间表示，n(x,y)表示加性噪声。为了将问题简化，暂时不考虑噪音的影响，则(1)方程简化为：

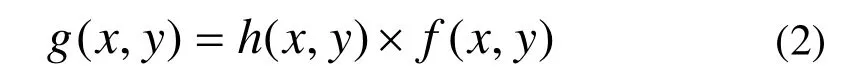
由于空间域的卷积等同于频域的乘积，所以(2)中各项经过傅立叶变换后，可以用等价的频域表示来表达：

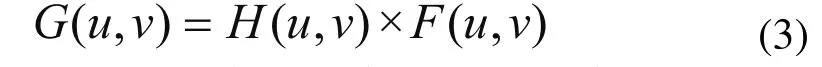
假设在成像设备的快门开启到关闭这段曝光时间T内图像运动距离为L，则：

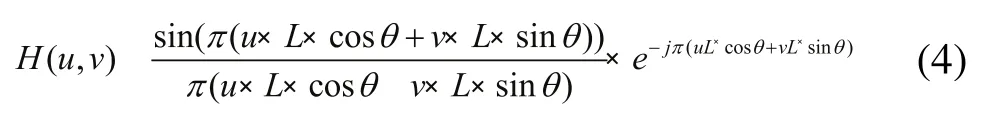
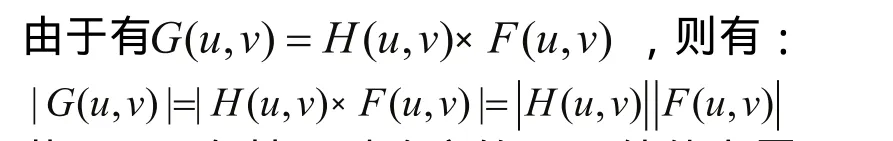
若H(u,v)在某一对确定的(u,v)处值为零，那G(u,v)在对应于该组(u,v)处也为零。也就是说G(u,v)和H(u,v)有相同的零点，G(u,v)的频谱也会有一系列与sinc(π×(u×cosθ+v×sinθ)×L)的零点对应的暗条纹。

但是模糊图像经傅立叶变换后的频谱图并没有什么直观的规律可循，这是由于傅立叶频谱的范围为[0,106]，甚至更高。当频谱显示在线性缩放至8比特的监视器上时，高值部分占优，导致频谱中低亮度值的可视细节丢失。于是进一步对频谱作对数变换，将其动态范围大幅度降低，使可视细节增加，方便观察。

模糊图像经过对数变换后，可以清楚地看到其傅氏频谱图中条纹的存在，但条纹的走向规律还不是十分一目了然，仍旧不便于观察研究。所以为了简化频谱的视觉分析，将原点的变换值由图像左上角的位置移动到频率矩形的中心位置。

这样条纹的走向更加清晰并且有规律可循了。将不同模糊方向的频谱进行比较分析,发现频谱图中条纹的方向与模糊图像的运动方向总是垂直的。只要能判断出条纹方向的角度，就可以计算出运动的角度。频谱图中条纹有着对称性，过图像中心的条纹宽度最大，其它条纹均匀对称分布在其两边。但如此多的条纹不便于确定角度，根据傅立叶变换的互异性[5]，再对经过位移处理后的频谱图做傅立叶变换。

沿水平方向成30度角运动的模糊图像频谱图经过对数变换、位移处理、二次傅立叶变换的频谱图如图1所示。

图1 图像频谱图

从图1(c)中可以观察到在图像的运动方向上，其对应的频谱有一条明显的亮线，检测这条亮线与水平方向的夹角便可以直接得出运动的方向了。若要对图4中的亮线测试角度，可以采取灰度求和的方法。以图像中心作为直线其中一个端点，在与水平方向0°至180°范围内计算每个角度对应直线的灰度值，哪个角度对应的直线灰度值最大，该直线必定就是那条亮线，角度便可以确定了。

2 Bresenham直线生成算法

要计算某条直线的灰度，实际上是求那条直线上所有点的灰度和。要快速确定哪些像素点落在同一条直线上，可以使用计算机图形学中的Bresenham算法[6,7]。此算法因由J.E. Bresenham提出而得名。因为在图形显示设备上显示直线，要由计算机计算出直线上要显示的各点坐标并逐个显示这些点。但由于显示设备所采用的设备坐标系是整数坐标系，直线上的各点，其坐标却未必正好位于设备坐标系的整数位置上，这就需要选择距该直线最近的像素点逼近显示该直线。

所谓“两点确定一条直线”，要在显示设备上生成一条直线，首先必须知道直线的两个端点A(xa,ya)和B(xb,yb),设xB≠xA, yB≠yA。接着便要确定AB之间直线上各个点的坐标。用Bresenham算法确定直线AB上的各点相应坐标，即把直线AB上的点在图形显示器上画出来的步骤如下：

1) 计算点A与点B之间的坐标差值，有Δx=xB-xA, Δy=yB-yA；记录Δx、Δy的正负，如果Δx＞0，则sx=1, 如果Δx＜0，则sx=-1; 如果Δy＞0，则sy=1, 如果Δy＜0，则sy=-1;

2)对Δ x，Δ y分别取绝对值，得Δx’=|Δx|,Δy’=|Δy|,比较Δx’与Δy’的大小，如果Δx’＞=Δy’则执行步骤3)，否则执行步骤4)；

3)计算偏差判别式的初始值d=2×Δy’-Δx’，确定直线其中一个端点A为当前处理的点，令x=xA, y=yA，重复以下步骤，直至循环次数i＞Δx’;

（1）根据x, y的值画出当前点；

（2）分别计算更新x、y和d的值，如果d＞=0，那么x=x+sx ,y=y+sy ,d=d-2×(Δx’-Δy’)，否则x=x+sx, d=d+2×Δy’,y的值不变；

（3）循环次数i递增。

4) 计算偏差判别式的初始值d=2×Δx’-Δy’，确定直线其中一个端点A为当前处理的点，令x=xA, y=yA，重复以下步骤，直至循环次数i＞Δy’;

(1) 根据x, y的值画出当前点；

渥巴锡之仲兄作为人质死于阿斯特拉罕，史载明确。具体拘禁之地、死亡之地，未留下史载，但人质不是普通的囚犯，将萨赖安置在作为当年阿斯特拉罕衙署所在地的小克里姆林宫、居住在这座白色大楼里，似也不失是一种合理的推测。若如此，小克里姆林宫也是土尔扈特人又一处伤心之地。

(2) 分别计算更新x、y和d的值，如果d＞=0，那么x=x+sx ,y=y+sy ,d=d-2×(Δy’-Δx’)，否则y=y+sy, d=d+2×Δx’,x的值不变；

(3) 循环次数i递增；

Bresenham直线算法是一个递推算法，根据当前已知点的坐标推算出下一个点的坐标。在每一步的推算中，都不需要对点坐标x、y的值进行浮点数和四舍五入运算，算法程序运行速度快，利于在硬件上实现。

3 算法的实现

可以总结出确定模糊运动方向的算法步骤：

1) 对模糊图像做傅立叶变换，将原点的变换值移动到频率矩形的中心；

2)频谱图做对数变换；

4) 计算频谱图中亮线与水平方向的夹角度数。

若要计算图1(c)中的亮线倾斜角度，可以图像中心作为直线其中一个端点，同时也作为图像坐标平面的原点，在与水平方向0°至180°范围内计算每个角度对应直线的灰度值，要计算某条直线的灰度值，实际上是求那条直线上所有点的灰度值之和。具体计算时可以以1°为单位递增逐个角度检验。若对角度精度要求比较高，可以在确定了大概的角度后，再以0.1°为单位递增角度值做更精确检测。将每一个角度的正切值计算出来后便可得到对应直线的斜率，有了斜率利用Bresenham算法可以快速确定某一角度值对应的那条直线上的像素点,哪个角度对应的直线灰度值最大，该直线必定就是那条亮线，该直线对应角度即为运动模糊方向。

当模糊运动方向为120°时，用本文提出的算法检测频谱图所得的数据如图2所示。

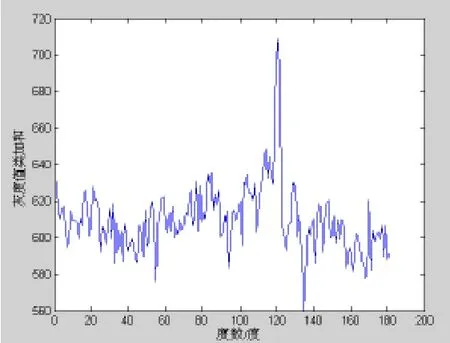
图2 0°至180°灰度值的计算情况

在Matlab 6.5的实验环境下，先对标准图像库中的图像cameraman.tif用imf i lter函数处理，生成不同运动方向的模糊图像，然后用结合Bresenham算法的角度估算方法分别判断各模糊图像的运动角度，实验结果如表1所示：

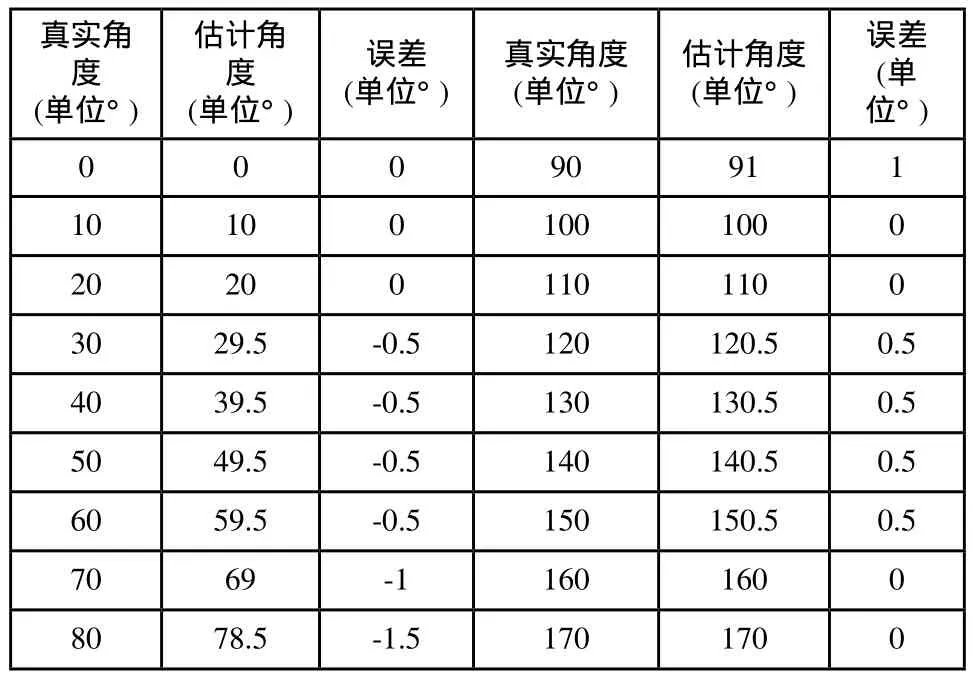
表1 运动模糊角度检测

实验证明，本文提出的运动模糊角度判别方法比较准确地判断出了图像运动的方向,误差不超过1°。

4 结束语

本文提出了一种结合计算机图形学中Bresenham 算法对图像的频谱图进行灰度求和进而确定运动模糊方向的算法。Bresenham 直线算法用于快速生成一条直线，将Bresenham 算法应用于判断图像运动方向的方法目的在于快速计算出某一条直线灰度值的和。

经过实验验证，本文提出的运动模糊角度判别方法比较准确地判断出了图像运动的方向。但这个算法能够判断的运动方向只是局限在0°至180°的范围内，也就是无法区分运动模糊的真实方向是θ=θ’还是θ=θ’+180°。若当运动模糊的真实方向是θ=θ’+180°,而采用θ=θ’作为参数进行图像恢复，所恢复的图像幅值不变，只是各像素位移发生变化[8]。

将本文提出算法的判断估算范围从0°至180°扩大到0°至360°是今后研究的方向。

[1] 潘琪.运动模糊仿真图像的正确生成 [D].广州:暨南大学.2005.

[2] 洪汉玉,陈以超.复杂背景运动模糊图像的盲复原算法研究[J].计算机与数字工程,2006,34(12):7-11.

[3] 谢伟,秦前清.基于倒频谱的运动模糊图像PSF参数估计[J]. 武汉大学学报(信息科学版),2008,33(2):128-131.

[4] 刘微.运动模糊图像恢复算法的研究与实现[D].北京:中国科学院.2006.

[5] 罗纳德·N·布雷斯韦尔著.殷勤业,张建国译.傅立叶变换及其应用[M] 西安:西安交通大学出版社,2005:24-26.

[6] 魏海涛.计算机图形学(第2版)[M].北京:电子工业出版社,2007:2-8.

[7] 金延赞.计算机图形学[M].浙江:浙江大学出版社,2003:134-140.

[8] 蔡慧敏,张艳宁,王志印,段锋,孙瑾秋.一种匀速直线运动模糊参数估计方法[J].计算机工程与应用,2008,44(19):175-177.