电磁斥力机构数学建模

贺开华



电磁斥力机构数学建模

贺开华

（海军驻湖南地区军事代表室，湖南湘潭 411101）

建立了电磁斥力机构的数学模型，在此基础上，对一组参数的电磁斥力机构分别进行了编程计算与软件仿真，仿真结果与编程计算结果非常接近，验证了数学模型的准确性。

电磁斥力机构，数学模型

0 引言

随着电力系统的发展，中压直流区域配电因其固有优势而得到重视与研究。与此同时，中压直流断路器的缺失成为制约其发展的瓶颈。

目前，大量研究的中压直流断路器主要为混合式断路器。该型断路器的关键技术之一为快速机械开关，其快速性对断路器的体积和成本有重要影响。

电磁斥力机构具有触动时间短（百微秒级）、分散性小（微秒级），可靠性高等优点，因此，目前在研究的混合式断路器中基本都采用电磁斥力机构。其原理示意图如图1所示a为励磁线圈，b为斥力盘，C为储能电容，储能电容对励磁线圈脉冲放电，与励磁线圈临近的斥力盘感应出与励磁电流方向相反的涡流，从而产生电磁斥力驱动触头运动。

电磁斥力机构的运动过程涉及到电磁场、涡流场和运动的多场耦合，快速准确地求解其运动过程是电磁斥力机构设计的重点与难点。日本三菱电气、山东大学和华中科技大学等公司或高校已进行了一部分研究[1-3]，本文主要从编程计算的角度出发，建立了电磁斥力机构的数学模型，并进行了仿真验证。

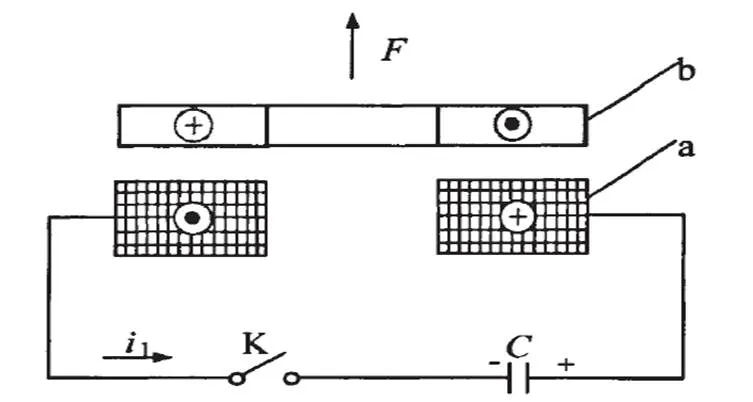
图1 电磁斥力机构的基本原理图

1 电磁斥力机构的数学模型

电磁斥力机构的电路拓扑如图2所示。

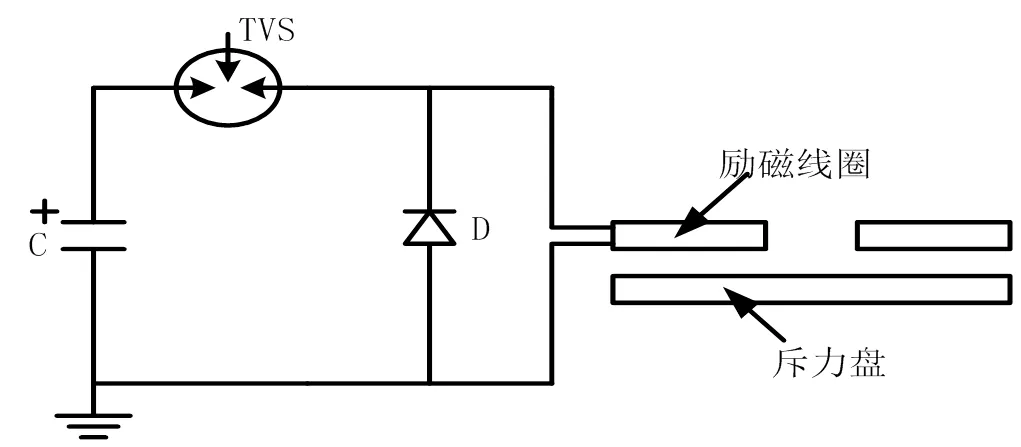
图2 电路拓扑

1.1 简化假设及参数描述

a) 励磁线圈的电感为1，电阻为1；

b) 斥力盘等效为一匝线圈，其电感为2，电阻为2；

c) 线圈与斥力盘互感为M，其初始值为M0。

d) 忽略线路的分布电感、电阻以及电容内阻。

1.2 运动过程建模

机构在合闸位置时，斥力盘受到来自合闸保持机构的合闸保持力，电容放电后，斥力盘受到的电磁斥力从零开始增加，当电磁斥力小于合闸保持力时，斥力盘保持静止状态，这个过程称为触动阶段；当电磁斥力F大于合闸保持力时，斥力盘开始向下加速运动，这个过程为斥力盘的运动阶段；在行程末期，缓冲装置对斥力盘提供缓冲，使其速度迅速下降，以减小分闸弹跳，保护真空灭弧室的波纹管，这个过程称为缓冲阶段。

由于在缓冲阶段动、静触头已达到必要的绝缘间距，对于开关灭弧性能影响较大的是触动阶段以及运动阶段的特性，因此本文仅对前两个阶段予以数学建模，分析该阶段的物理过程。

a) 触动阶段

触动阶段时间一般是极短的，外电路还处于电容放电阶段，二极管组件相当于开路，其电路图如图3所示。

图3所示电路可用微分方程组(1)描述：

然后根据方程(3)求解出斥力盘的触动时间1。

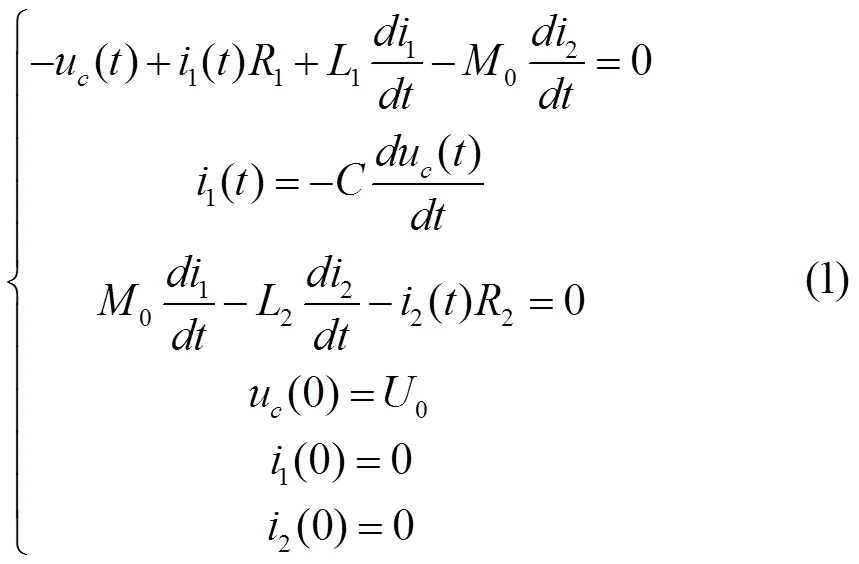
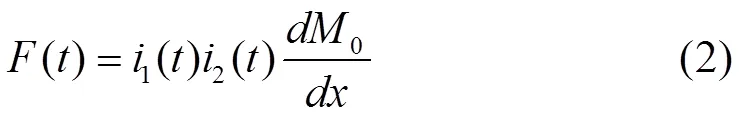
1时刻对应的励磁线圈电流值、斥力盘感应涡流值以及电容电压值以作为下一阶段的初始条件用于下一阶段的分析，它们分别为1=1(1)、2=2(2)和2=c(1)。

b) 运动阶段

运动阶段根据二极管组件是否导通又需要分为两步进行求解。

二极管组件导通之前，电路图没有变化，依然如图3所示，但是，与之前有所不同的是，互感M不是固定不变的，而是随斥力盘的运动而发生变化的。这个过程可以用微分方程组(4)来描述：

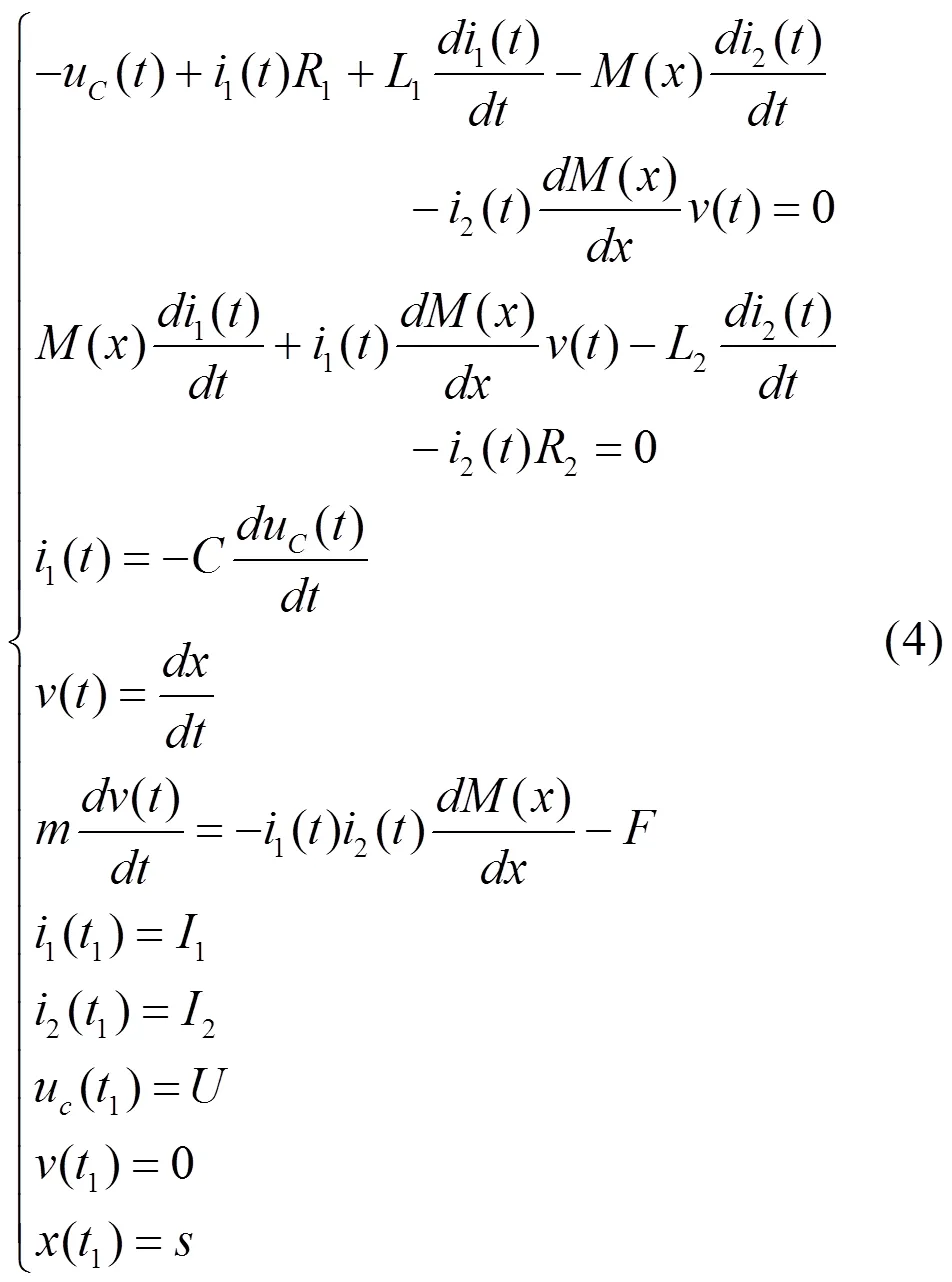
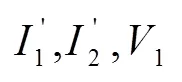
从时刻t2开始，电容电压降为零后不再被反向充电，电感电流通过二极管组件续流，电路进入续流阶段，此时，电路图如图4所示，

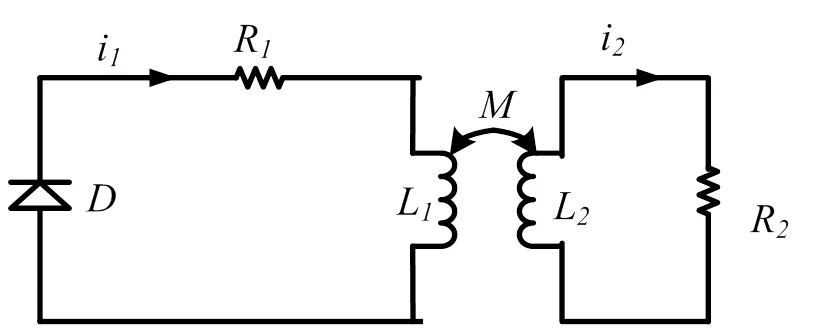
图4 续流阶段电路图

续流阶段的微分方程组为方程组(5)：

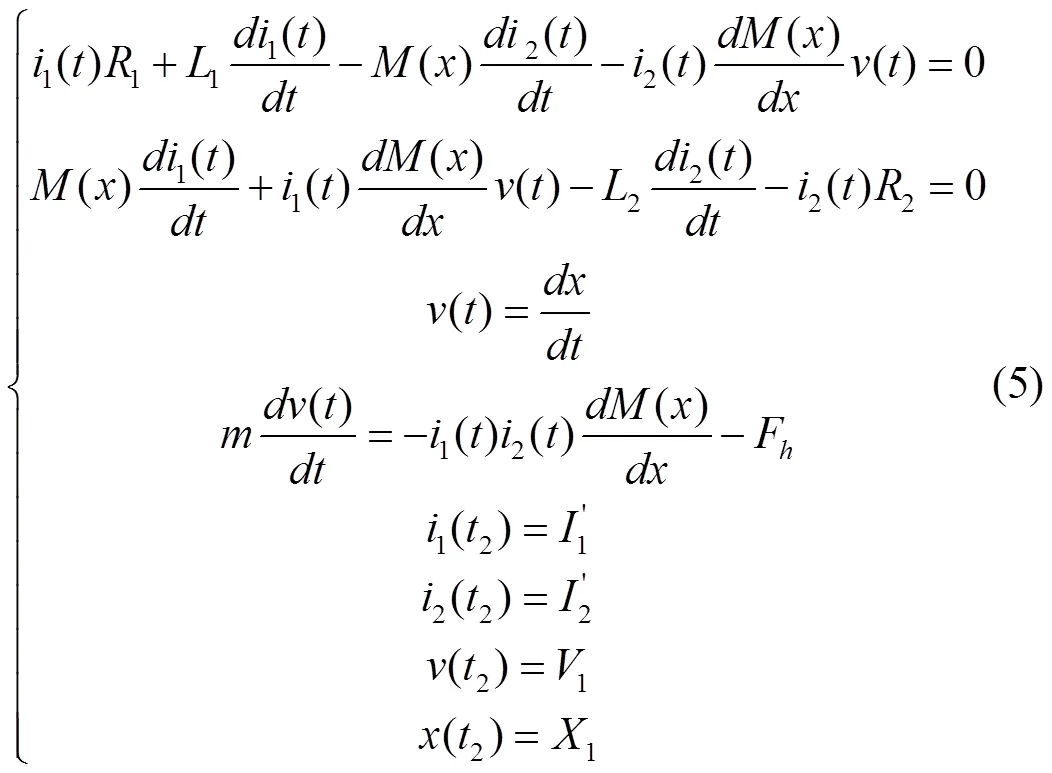
设置好终止条件，采用Runge-Kutta法求解微分方程组(5)。可以得出续流阶段的电流、速度以及位移曲线。

最后，将三组微分方程组的求解结果进行整合，就可以得出整个运动过程中的电流、电压、速度以及位移的曲线。至此，完成了斥力机构整个运动过程的数学建模。

2 编程计算及ANSOFT仿真验证

选取一组电磁斥力机构参数分别进行编程计算及软件仿真，编程采用MAPLE进行，仿真则采用ANSOFT MAXWELL瞬态场进行。结果分别如图5和图6所示。

可以看出，两种方法算得的电流曲线基本一致，证明本文所建立的电磁斥力机构数学模型基本准确，可以用来进行电磁斥力机构的设计分析。

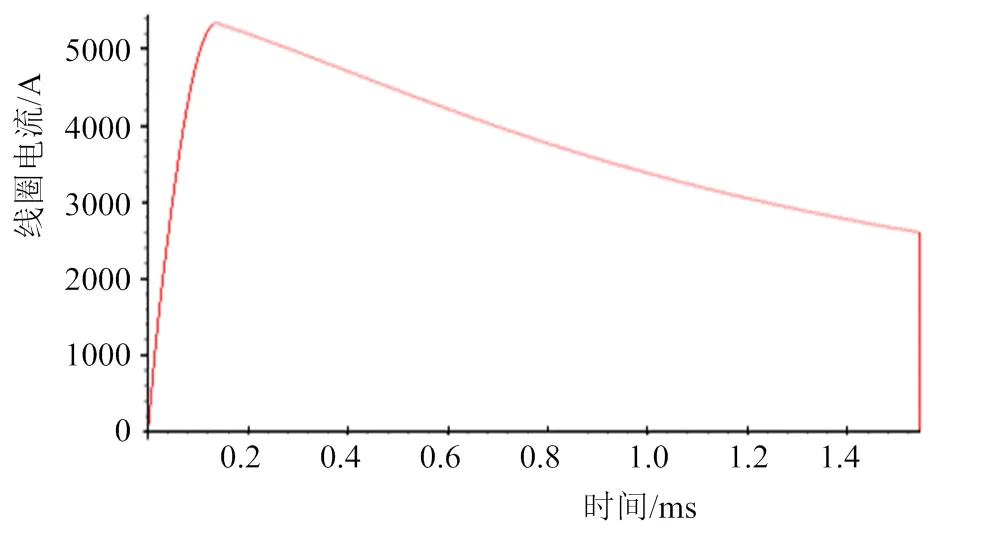
图5 线圈电流计算曲线

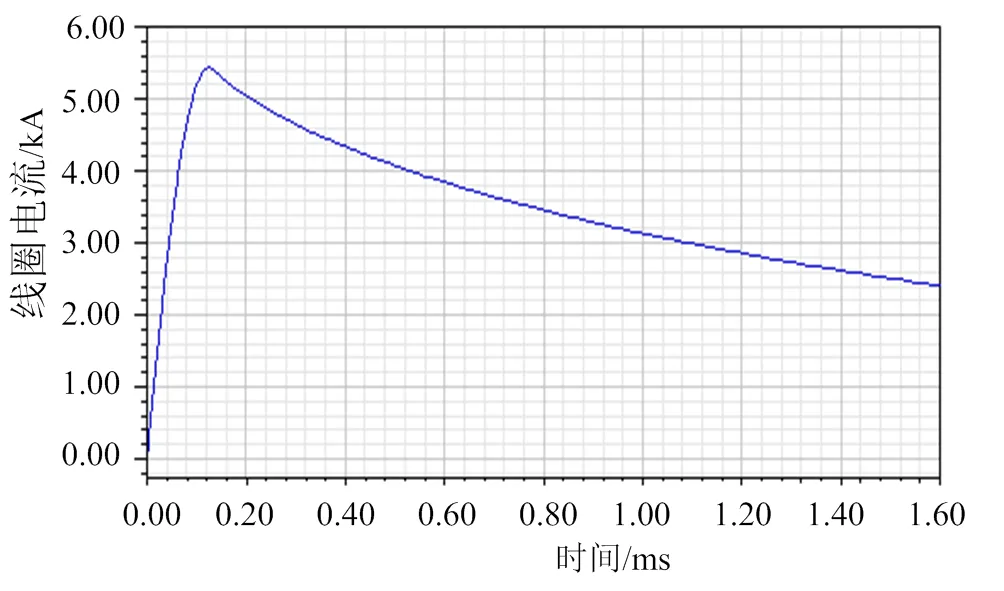
图6 线圈电流仿真曲线

3 总结

本文通过合理的简化假设，对电磁斥力机构的运动过程进行了数学建模，并通过电磁场仿真软件ANSOFT MAXWELL对该数学模型进行了计算验证，结果证明数学模型基本准确，对斥力机构的设计分析有一定的指导意义。

[1] TOSHIE TAKEUCHI, KENICHI KOYAMA, MITSURU TSUKIMA. Electromagnetic analysis coupled with motion for high-speed circuit breakers of eddy current repulsion using the Tableau Approach. Electrical Engineering in Japan, Vol. 152, No. 4, 2005.

[2] 李庆民, 刘卫东, 钱家骊. 电磁推力机构的一种分析方法.电工技术学报. 2004, 19（2）: 20-24.

[3] 王子建, 何俊佳, 尹小根. 基于电磁斥力机构的10 kV 快速真空开关. 电工技术学报, 2009, 24(11): 68-74.

Mathematical Modeling of the Electromagnetic Repulsion Mechanism

He Kaihua

(Naval Representatives Office in Hunan, Xiangtan 411101, Hunan, China)

TM561

A

1003-4862(2013)12-0062-03

2013-09-24

贺开华 (1966-)，男，高工。专业：电机电器。