洗尽铅华 返璞归真

郭广成，中学高级教师，哈尔滨市复华小学校教导主任。曾获得全国优秀实验教师，全国重点课题先进个人，黑龙江省优秀教师、数学教学能手，哈尔滨市优秀教师、数学学科带头人等荣誉称号。独树一帜的“寻根导学 理趣交融”的教学风格受到推崇，在各级各类教学评比中均取得优异成绩：第九届全国深化小学数学教学改革观摩交流会一等奖；全国第三届学具应用教学评比一等奖；第三届全国“现代小学数学”课堂教学评比一等奖等。

黑龙江省首位参与人教社小学数学教师教学用书中课堂教学录像的教师，他的课堂教学录像作为小学数学学科配套教学资源全国发行。

课程改革十年了，回顾十年，阅读《数学课程标准（2011版）》若有所思，记录下来与大家分享！

当《数学课程标准（2011版）》出来之后，没来得及认真研读的时候，我就问自己：这十年我们做了些什么？

细细品味——无论是对还是错，是成还是败，我们是成功者，因为我们在这一过程中得到历练了，都成长了。在不知不觉中我们的观念发生了变化，我们的教学行为也发生了变化。回头看一看我们教过的一批批学生，无论是从人格上还是学业上也发生了变化，他们较以往更富有鲜活的个性了。

想到这些，我不由得又问自己：课程标准为什么要进行修改呢？是否在“折腾”呢？

带着这样的问题我开始研读《数学课程标准（2011版）》。

“对比研读”是最容易悟出道理的！

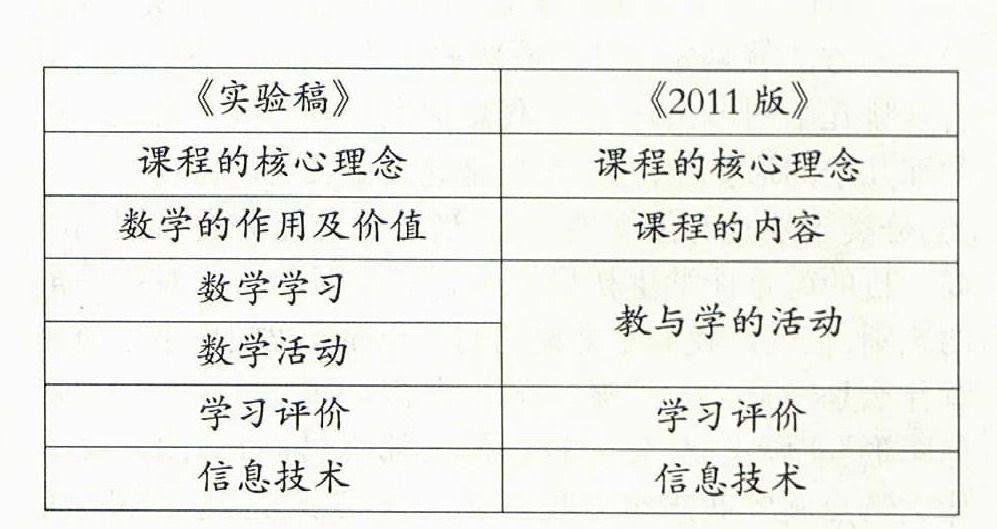
两个版本课程的基本理念的对比如下：

《实验稿》提出“人人学有价值的数学，人人都获得必需的数学……”到《2011版》变成“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展……”

对比之后，我们不难看出，《实验稿》是在让我们全都动起来，动起来了大家都会在不知不觉中发生变化的，当量达到一定程度的时候，那就一定要发生质的变化了。于是，《2011版》的修改就是要我们作更深层的思考，做更实效的工作。

回头看一看，这十年，我们经历了“木然——冲动——冷静”这样一个变化过程。课改初期，无论是“情境”的倡导，还是“数学生活化”的推崇……这一切都是在制造数学课堂教学的不平衡，当不平衡出现时，必然会拉动对数学本质的研究，这就是一个螺旋上升的过程。那么，就数学说数学，我们一直不变的是对数学本质的探索，随着对数学本质研究的深入，数学课堂教学产生的“双基”变“四基”的变化也是情理之中的。作为第一实践者——数学教师，我就谈一谈自己在研究数学本质方面的一点儿想法。

那么，什么是本质呢？

本质：指事物本身所固有的、决定事物性质、面貌和发展的根本属性。而事物的本质又常常是隐蔽的，是通过现象来表现的，不能简单、直观的认识，人们必须透过现象掌握本质。

“备课要备知识的根！”这个“根”指的是知识的本质。做一个数学老师就要做到“透过现象看本质”。对于数学知识，我们一定要做到“刨根问底”掌握其来龙去脉，才能运用自如、游刃有余。

“探本求源”秘技一：分清领域，选定策略

比如 “对称图形”教学内容，大家在看教材的时候，会发现教材只是给了我们一些活动的素材，并没有给我们更大的启发。我也曾一度不知所措。后来，我想：这节课是“对称图形”，它的本质在哪里？它是空间与图形（现在是几何与图形）的领域，它又是怎样产生的呢？它是人们在观察图形的时候，发现这些图形有着与众不同的特点，所以才归纳出“对称图形”。由这个角度去考虑，那它又应该属于“统计与概率”中的“分类”的范畴。怎么引入呢？我想最好的方法就是先让学生看一些图形，让学生说一说，最喜欢哪几个图形，为什么。我想学生一定会说：“喜欢对称的那几个图形！”因为人大多是完美主义者。再让学生分类，分类当然是有依据地分类，当学生交流分类依据的时候，目的就是让学生初步地找到对称图形与非对称图形的区别，也就是我们常常说的初步建模。我们再来思考究竟什么是“对称图形”呢？在小学范围内，我们学习的“对称图形”实际上是“轴对称图形”，那么，轴对称图形又有什么特点呢？我想至少我们要从这三个方面去分析：大小、形状、位置。具体地说一说，如果一个图形是轴对称图形，那么它一定是具有能够在一条直线的两边出现，大小相等，形状相同，位置相对的属性，而这三个方面是缺一不可的。那么，在引出轴对称图形和对称轴这两个名词后，我们所有的活动就应该围绕着这三个方面去进行，至少在下面的活动中，要有图形“大小相等，形状相同，位置不相对”和“形状相同，位置相对，大小不同”以及“位置相对，形状相同，大小不相同”三种不是轴对称图形的图形进行对比，才能让学生通过甄别，更深层次地去掌握轴对称图形的特点，才能更好地去判断轴对称图形。

刚刚我说的轴对称图形是人们在分类中产生的，但它必竟还是“空间与图形”（现在是几何与图形）的知识，那么在这里我们一定要锻炼学生的空间想象能力，而这一课中最有利的训练就是已知轴对称图形的一半根据对称轴去画出完整的图形。这样的训练题对于思维类型比较好的同学不是什么难题，而对于形象思维不好的同学则是一大难点，那就是方法论的问题了。这就需要老师设计一个环节，让老师和同学们共同去发现，用最有效的办法去解决这个问题。其实，说是师生共同去发现，实际上老师心里要有数，如果老师心里都没数，这也行，那也行，那课堂一定乱了，课堂效果也一定不会好。我们要做的只不过是让学生在众多的方法中去选择那个不一定是最简单的，但一定是最对的方法。我们在探讨的过程中，发现一个最好的方法，必须引入一个名词，那就是关键点（有的人把它叫做对称点）。实际上在方格中，让学生画的图形，大多都是由若干个线段围成的图形，而每两条线段的交点就是那个关键点，只有关键点确定了，才能确定线段。这里还有一个依次连接的问题，那就让学生做到确定两点之后就进行连线的方法。所以，我们想最好的方法就是分三个关键步骤解决这个问题：1.描关键点2.顺序连线3.细致涂色。我想要是按照我们上面分析的内容进行课堂实践，无论你是用什么方法，用什么活动，即使是最拙劣的讲解，课堂效率也一定能够提高。

因此，确定了领域也就是确定了教法，也就抓住了数学知识的本质。了解了真正的应用策略，也就能确定数学活动的安排；抓住了数学知识的本质才能知道知识的训练点，也就能确定课堂习题的编排。那么，上一节好课，也就不难了。

“探本求源”秘技二：制造冲突，放手去学

我们现在用的教材中，有很多重要的知识，学生学习起来很迷茫“为什么要学这个知识？”“学来是做什么用的？”学生学习的时候，只知道教材里有的就得学，老师教的就得会，学了期末就得考。这样学习起来很被动，也没什么兴趣。没有需求就没有动力。我觉得我们现在的教材没讲清，我们就得通过我们的教学让学生清楚。比如，“求平均数的教学”教材中是以摆小木块的游戏引入的，得到“移多补少”，再通过一两道实际问题，弄清除了“移多补少”的方法适合比较容易的问题，而用“总数除以份数等于每份数”的方法则是比较简便的。但是我们想一想，学生们虽然学会了这种方法，但是他们知不知道，为什么会有平均数这个知识呢？分析“平均数”这个概念是人们为了合理地比较和分配而产生的，正因为这样才会有“平均每人植树2.3棵”这样的数字，也就是说它是一个统计的概念。那我们就必须得让学生用统计的方法去学，只有这样学生才知道为什么会有“平均数”，它是做什么用的。课堂上先把学生分成若干个小组，每小组人数不等，教师说：“我们分成了几个小组，今天我们就要在这里进行一次计算比赛，我们要评比出计算最优秀的小组。大家说，以什么作为评价标准呀？”学生说：“看哪一小组做对的题多！”“很好，现在这里有一些相同的题，每人一份，在规定时间内，大家同时做同时停，然后，我们再评，这样公平吗？”学生说：“公平！”“好，开始！”一段时间后，做出了答案，大家一评，做对题最多的小组出来了。就在我要宣布“最优秀小组”的时候，有人提出：“这样不公平！”我问：“为什么不公平？”“因为人数多的组做对的题就多，人数少的组做对的题就少，所以不公平！”“那怎样评才算公平呢？”有学生说：“让每个小组的人数相等才行。”我又说：“这个主意很好，那我们就分一分吧。”这时候班级就乱起来了，“仨一帮俩一伙”地分起来，时间一分一秒地过去，还是没有结果。这时学生犯难了，我又问：“同学们，时间有限呀，这样下去可不行呀！”有一个学生说：“老师，咱们班59人，不好分呀！”我又说：“那怎么办呢？”一个学生大声地喊出来：“算一算，每一小组中平均每个人做对多少道题再比较才算公平！”“那怎么来算出平均每个人算对的题多呢？“我们得先知道每个小组一共做对了多少道题和每个小组有多少名同学，这样才能得到平均每一位同学做对多少道题，这样就行了。”“那好吧，我们再来比一比吧！”……一段时间过后结果出来了，我又问：“同学们这个结果公平吗？”答案是肯定的。

其实，学生重分小组的过程就是“移多补少”的过程，而最终解决问题的方法就是这节课学习的重点。

于是，学生就这样在统计比较中，感受了“平均数”，找到了求“平均数”的方法。抓住“平均数”的数学本质，故意制造冲突，把学生的心牢牢地抓住，让学生从“知识的本质”学起。正像我们常说的一句话：“学得明白，学得实在。”

“探本求源”秘技三：中心问题，殊途同归

每一个教学内容都会有一个中心的问题，这个中心问题一定是指向数学本质的。围绕这个中心问题学生就一定会展开有效的数学学习。

我们来看“复式条形统计图”这一教学内容的片段：

师：同学们，我所教的班级本学期开展了争星评比活动，班长每月进行一次统计，并向全班同学汇报。看（课件），这是9月份获星人数情况统计表，都统计了哪几个项目呢？

生：纪律、卫生和学习。

师：除了用统计表，还可以怎样表示这几个项目数据的多少？

生：用统计图。

师：我们学过什么统计图？

生：条形统计图。

师：（板书：条形统计图）我们班的班长也制成了条形统计图，大家看（课件），名称谁能大声读出来？

…………

师：你能发现哪些信息？

生1：纪律、卫生和学习各有多少人获星。

生2：学习获星人数最多，卫生最少。

师：你是怎么知道的？

生：看数据大小或看直条的长短。

师：那你说说条形统计图和刚才的统计表相比，有哪些好处。

生1：看得清楚。（板书：一目了然。）

师：还有补充吗？

生2：好比较。（板书：便于比较。）

师：看来同学们对条形统计图的知识掌握得真不错，10月份的评比也结束了，我们来看（课件），与同桌交流一下你发现的信息。

…………

师：这两张统计图（课件）清晰地反映出了两个月各个项目的评比情况，相信大家也发现了从9月份到10月份，各项都有了一些变化（手指两张图），你能不能想个办法让我们一下就能看出情况的变化呢？

生：可以把两张统计图合成一张。

师：把两张统计图合成一张，这个方法你们觉得怎么样？

生：很好。

师：这可真是个好办法，接下来我们就在手中的图纸上动手尝试一下，尽量做到让别人能看明白你制图的意思，做得快的就有机会得到展示，开始吧！

…………

这一教学片段的中心问题就是怎么比较更方便。学生在我的追问下，产生一个个思维的火花，在实践和探索的过程中，呈现“图例”这一知识增长点也是必然的结果。可见，抓住中心问题，学生就会一步步走进探究数学本质的“陷阱”之中，其效果是可想而知的。

其实，我想与大家交流的是：数学老师应该终身对数学本质进行探索。我们在课程改革的过程中不断地拉动自己的内需，引发更深层次的思考，会成为课程改革的最终受益者，而受益最多的是我们的学生。所以，课改十年后，我的所得就是“洗尽铅华 返璞归真”，做最实、最真的数学是我矢志不渝的追求。