基于FPGA的多路无串扰超声测距系统的设计与实现*

孟庆浩，边旭东，扈佳林，曾 明

(天津大学，电气与自动化工程学院，机器人与自主系统研究所，天津300072)

超声换能器因具有尺寸小、价格低，且硬件电路容易实现等优点，在工业测量和移动机器人导航等领域得到了广泛应用。目前用于移动机器人的超声测距系统至少存在两方面的问题，一是测距精度偏低，二是多个超声换能器同时工作时存在相互干扰，即串扰［1］。基于渡越时间法测距的关键是回声时间的准确获取，但在测距过程中，由于噪声等其他信号的干扰和回声信号在空气中幅值的衰减和变形等原因，导致渡越时间难以准确捕获。由于超声换能器的波束角有限，为了提供360°范围的环境信息，需要将多个超声换能器组成环状。但多个换能器同时工作，就可能产生串扰现象，即某个换能器接收到其他换能器发射的超声，从而导致测距错误。

为了提高渡越时间捕获的准确性，国内外一些学者提出了测量或估计渡越时间的方法。最简单的渡越时间捕获方法为阈值法(Threshold Method)［2］，但由于回声幅值的变动很难预测，且回声信号到达阈值的时刻迟于实际回声信号的起始时刻，所以这种方法准确度不高。Huang等［3］提出了基于二值频移键控(BFSK)的相移法测距，该方法的测距精度较高，但实时性较差，且硬件实现成本高。姚振静等［4-5］基于平方根无迹卡尔曼滤波估计了单脉冲超声测距系统的渡越时间。考虑到卡尔曼滤波的收敛速度与初始状态有关，该文提出了多初始状态的平方根无迹卡尔曼滤波算法用于渡越时间估计，并通过计算机仿真验证了所提算法的可行性和准确性。但这种算法计算复杂程度高，不能满足实时性要求。在计算自相关函数时，黄增荣等［6］采用数字相关方法确定渡越时间，并用并行数字相关技术代替傅里叶变换算法，减少了数据处理时间和FPGA资源，通过仿真进行了验证。葛万成等［7］采用两步相关法计算渡越时间，减少了处理时间。潘仲明等［7］提出了一种粗、精两步相关法计算互相关函数，并由此确定超声波的射程时间，显著地减少了超声测距系统的数据处理时间，因此采用普通单片机可实现大量程超声测距。文献［9-10］设计了结构紧凑、功耗较低且具有超声收发一体功能的硬件系统，为超声测距提供了稳定、可靠的硬件平台，并建立了该测距系统基于自回归滑动平均(ARMA)的数学模型，为仿真研究提供了模型支撑。文献［11］采用极性相关算法并利用FPGA实现了实时距离信息的测量，测距效果良好，但FPGA中占用资源较多。

为了消除多个超声换能器同时工作带来的串扰问题，Jörg等［1］通过脉冲压缩的方法赋予每个超声换能器唯一的标识，并挑选合适的伪随机码，在接收端采用相关匹配法分辨回波信号是否为自身发出的超声波。Fortuna等［12］基于混沌脉冲位置调制方法研究了超声串扰消除问题。文献［13］和［14］分别采用巴克码和格雷码消除超声串扰现象。但巴克码的有限长度和格雷码实现的复杂性在某种程度上限制了这两种编码在超声扩频领域的实际应用。为减小回声相关的计算量，Nakahira等［15］采用数字极性相关方法，把连续模拟信号的乘法运算转换为简单的数字运算，大大简化了运算量和硬件开销。程晓畅等［16］采用m序列结合幅移键控的调制方式研究了超声扩频测距系统，提出了一种基于快速傅里叶变换的伪随机码包络相关快速时延估计算法，降低了运算量。杨斌虎［17］采用m序列结合数字信号处理器研究了超声测距方法。孟庆浩等［18-19］采用遗传算法优化伪随机脉冲位置调制和混沌脉冲位置调制序列，有效地抑制了超声串扰现象。杨雪［20］将4种模拟调制方法(即混沌脉冲位置调制、混沌脉冲宽度调制、线性调频及非线性调频)和3种数字调制方法(即二值幅移键控、二值频移键控和二值相移键控)与多种伪随机编码方式结合构造出了脉冲序列激励超声换能器，并用回声相关度、能量效率等性能指标进行了比较，找出了适合扩频超声测距系统的编码和调制方式，有效地避免了超声串扰，提高了有效测距范围。但该文并未将结果应用于实际超声测距系统中。

本文在前期的超声编码与收发电路设计的工作基础上，给出了一个基于FPGA的六路无串扰超声测距系统的设计与实现方案。FPGA作为整个系统核心，用于完成超声激励编码的存储与发射、回声信号极化相关、计算/显示距离及向上位机发送数据等任务。实验表明，本文给出的设计方案可保证六路超声测距单元实时地工作，相互之间的串扰可有效地消除，在35 cm～420 cm的范围内，可实现10 mm的测距精度。

1 无串扰超声测距原理

无串扰超声测距的关键包括超声编码/调制及渡越时间捕获。在得到渡越时间t后，可采用式(1)计算距离。

式中，D为超声换能器与障碍物之间的距离;C为超声波在空气中的传播速度。在常温常压下，空气近似为理想气体。超声波在理想气体中的传播速度可用式(2)计算。

式中，r为定压分子热容量与定容分子热容量的比值，R为气体常数，T为绝对温度，u为气体的分子量。对于一定的气体，r和u为定值;当温度恒定时候，可以认为超声波在空气中传播的速度C为一个定值。这样，渡越时间的准确性决定了测距的准确性。

1.1 超声编码与调制

为了有效抑制超声串扰并扩大有效测距范围，本测距系统引入了扩频和编码思想，给每路超声换能器激励序列赋予独特的编码。同时，为了简化硬件电路，降低程序复杂度，保证系统实时性，测距系统采用脉冲序列激励超声换能器。

基于超声扩频脉冲编码测距原理，本文总结了杨雪［20］研究的数字调制激励序列构造方法，即将6种伪随机编码和3种数字调制方式两两结合，从而得到18种扩频脉冲编码激励序列。6种伪随机编码序列包括m序列，混沌序列，Gold序列，Balanced Gold序列，Legendre序列和Hall序列;3种数字调制方式包括二值幅移键控(BASK)、二值频移键控(BFSK)和二值相移键控(BPSK)。为了从中挑选出一种最适合超声测距应用的激励序列，本文从回声序列相关特性、激励序列与回声序列的能量特性两个方面对这18种数字激励序列进行了评价。

本文用相关度评价回声序列的相关特性。相关度R定义为:P路超声换能器的回声序列集中，所有序列两两互相关的函数峰值中的最大值和各序列自相关的函数旁瓣值中的最大值，二者中较大的值为回声序列的相关度。其表达式为:

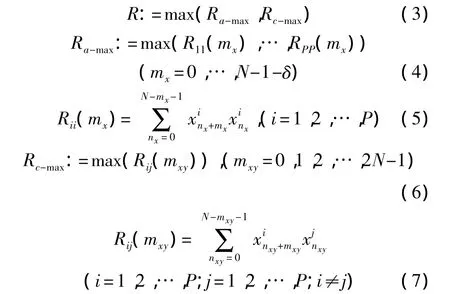
其中，Ra-max为P个超声换能器的回声序列自相关函数的最大旁瓣值，Rc-max是所有超声换能器的回声序列互相关函数峰值的最大值;Rii(mx)为第i路超声换能器回声序列的自相关函数，Rij(mxy)为第i路超声换能器的回声序列与第j路超声换能器的回声序列的互相关函数;P为多路超声测距系统中包含的超声换能器的个数(本文中P=6)，δ是回声序列自相关函数主瓣宽度的一半，N为回声序列的采样点数;为第i路超声换能器的回声序列中第nx个采样点取值为第j路超声换能器的回声序列中第nxy个采样点取值。

在测距过程中，同一类编码调制方式组合生成的激励序列所产生的回波自相关函数的旁瓣值越小，互相关函数的最大峰值越小，即回声序列相关度越小，相关特性越优良，则通过相关法越容易识别出与自身匹配的回声序列，也越能准确地捕捉到主瓣峰值对应的渡越时间点，从而防止串扰现象和错误测距信息的产生。

能量特性的评价指标为激励序列能量值及能量效率。超声测距系统的激励序列所携带的能量越大，可测量的距离范围越大;回声序列的能量越高就越容易被接收端检测到;能量效率越高，测距系统的能量利用率越高。

定义信号v的能量为

其中，vi(i=1，2，…，N)为信号 v的第 i个采样点取值，N为采样点数，RE为等效电阻。

将能量效率η定义为回声序列与激励序列的能量之比，即

其中，ER为回声序列能量值，ET为激励序列能量值。在测距过程中，激励序列能量越高，且能量效率越高，才能保证系统的有效测距范围越大。

综合考虑回声序列相关度，激励序列与回声序列的能量/能量效率的性能分析比较结果，从中可以得出Gold序列与BFSK调制方式的组合在各方面的综合性能最好。所以本文设计的超声测距系统中选用Gold序列与BFSK调制结合的脉冲编码数字调制序列激励六路超声换能器。图1和图2分别为Gold编码BFSK脉冲激励序列与其回波序列。

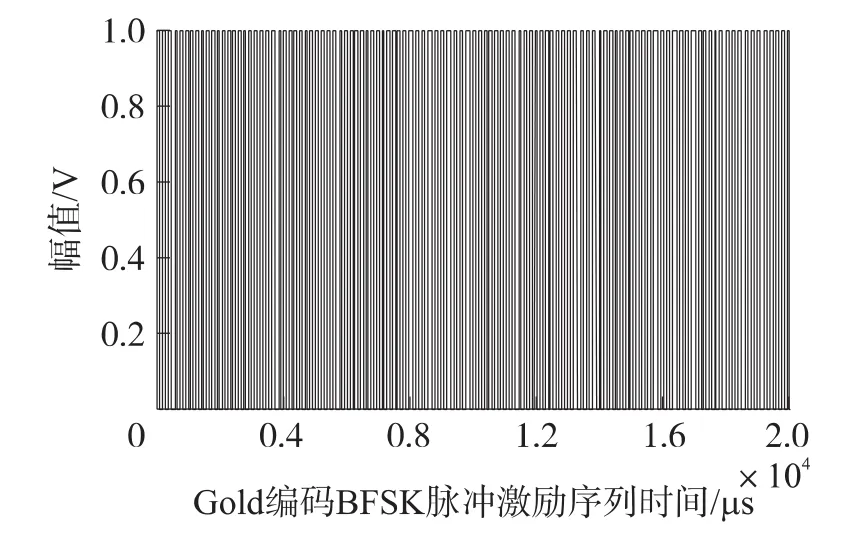
图1 Gold编码BFSK脉冲激励序列

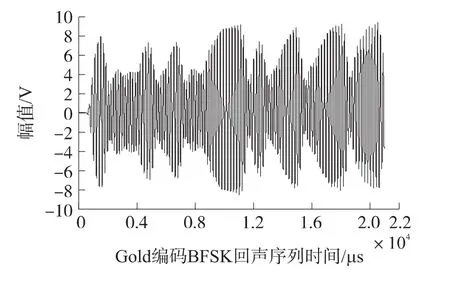
图2 Gold编码BFSK回声序列

1.2 渡越时间捕获

超声测距中获取渡越时间的关键在于准确地估计回声信号起始位置。本文采用相关检测法估计渡越时间。该方法是指超声测距系统接收端的回声信号与预先存储的标准回波信号进行匹配滤波，进而确定渡越时间。假设参考信号为x(t)，回声信号为y(t)，那么它们之间的互相关函数定义为:

当互相关函数取得最大值的时候，τ的取值即为渡越时间。但是由于相关算法计算量大，计算时间较长，导致超声测距系统的实时性差。

为了简化在FPGA中计算的复杂度，加快测距系统实时性，应用了过零极化相关算法［11］。该算法先将模拟回波极化为二值序列，这样就将普通相关算法转化为极化相关算法，即用同或、加法运算代替模拟相关复杂的卷积运算。

对于两个离散时间序列f1(k)，f2(k)，它们之间的互相关函数可以定义为如下:

而f1(k)的自相关函数可以定义为:

为了进一步简化计算量，该算法提出针对数据段进行运算的思想，而不是针对数据位进行运算。首先对数据块进行划分，其块之间的边界点就是本地码(标准回波信号)数据突变时刻点，由1变0或0变1的时刻点，因此把此数据突变时刻称为过零时刻。假设x0表示本地码数据，y(k)表示k时刻与本地码进行相关运算的数据，整个本地码x0中按照上述定义划为M段，则在k时刻x0和y(k)的相关结果和在(k-1)时刻x0和y(k-1)的相关结果的关系可表示为:

其中，Rxy(k)表示 k时刻 x0和y(k)的相关结果;表示k时刻第i个数据段最左端的数据位和y(k)最左端的数据位作同或运算;表示(k-1)时刻第M个数据段最右端的数据位和y(k-1)最右端的数据位作同或运算。从上式中可以看出，如果已知(k-1)时刻的相关结果，只需在k时刻对本地码x0的第一位数据、最后一位数据和过零时刻点的数据与待相关信号y的对应位数据作同或运算，即可求出k时刻的相关结果。通过理论与实验验证，过零极化相关算法与直接相关算法相比计算结果几乎相同［9］，但过零极化相关只需在过零时刻，本地码的最左端以及最右端进行运算，运算量减少了90%，大大减少FPGA的计算量。

本测距系统中回波信号时间长度为2 ms，采样频率为1 MHz，采样后得到2 000个回波数据，这2 000个数据存储在FPGA中。如果采用一般极性相关算法，那么需要对这2 000个采样数据逐位进行计算，这要占用FPGA中大量的逻辑模块资源。而采用过零极化相关算法，只需要找出过零时刻，采样数据最左端和最右端的数据(约为200个)进行计算，运算量大大减少，并且极大减少FPGA中存储器资源和逻辑模块资源的使用。

2 六路超声测距系统的设计与实现

本文设计的无串扰超声测距系统由六路相互独立的测距单元组成，原理如图3所示。每一路测距单元则由FPGA数字处理模块和超声收发电路及信号调理电路两大部分组成。其中FPGA数字处理模块控制超声收发电路发射与接收超声波，信号调理电路则对超声回波进行滤波、放大、幅值调节，最后将其转换为数字信号送入FPGA数字处理模块中与参考信号进行过零极化相关运算，识别回波并捕获渡越时间，进而计算出超声换能器到障碍物的距离。

FPGA把每路测距单元计算得到的障碍物距离信息通过RS-232接口，传输到上位机，然后障碍物距离信息显示在用户使用界面。

图3 无串扰超声测距系统整体示意图

2.1 超声收发电路及信号调理电路

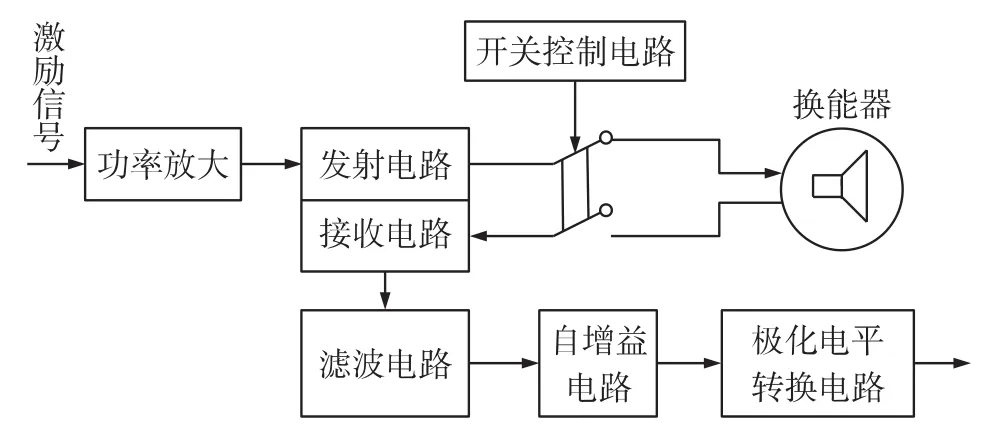
图4 单路超声收发电路及调理电路框图

超声收发电路及信号调理电路是由发射/接收一体电路、滤波电路、自增益电路与极化电平转换电路组成，如图4所示。本系统设计采用SensComp公司生产的600系列静电超声换能器。由于从FPGA发射出来的激励信号功率太小，无法直接激励超声换能器。激励信号需通过以变压器为核心的功率放大电路进行放大，得到由200 V直流偏置和200 V交流电压叠加而成的驱动电压，从而激励超声换能器发出超声波。为了使硬件结构紧凑，系统采用超声收/发一体结构，通过 FPGA控制光电开关AQW216切换超声换能器的发射与接收状态。

超声回波在接收过程中不可避免地引入外部环境噪声，因此首先对其进行滤波处理。由于系统采用的超声换能器工作频带在40 kHz～70 kHz，所以采用MAX275设计了该频带范围的带通滤波电路。

众所周知，超声波在介质传输过程中会呈指数形式衰减，且传播距离越长衰减越大，为此，本文使用了基于PID的自增益电路［9］，它的作用是根据回波幅值的大小，自适应地调节放大倍数，使来自不同距离的回波信号能够与参考信号在波形上尽可能相似。这样回波信号在FPGA中与参考信号进行过零极化相关计算得到的结果更准确。超声收发电路及信号调理电路的细节可参考文献［9-10］。

回波信号经自增益电路之后仍然是模拟信号。为了满足过零极化相关算法对过零点数据的需要，系统采用迟滞比较器和开关管电路对其进行极化处理和电平转换，从而得到满足FPGA电平标准的数字信号，用于FPGA的后续处理和计算。

2.2 FPGA数字处理设计

本测距系统中的FPGA主要完成3个工作，一是储存并发送六路含有独特标识的脉冲编码数字调制激励序列;二是对六路经硬件系统处理后的回波信号与本地码进行相关运算，得到距离信息;三是在计算距离信息的同时将其通过RS-232接口传输到上位机，在用户使用界面显示。为了协调好六路测距单元正常工作，使其得到正确测距结果，采用有限状态机的设计思想对其进行管理。将FPGA内部所要完成的任务分为4个状态，分别为State1，State2，State3和State4。其中State1为空状态。具体工作分配为:

(1)State2状态的工作是系统初始化。

(2)State3状态的工作是发送脉冲编码数字调制激励序列。

(3)State4状态的工作是回波识别，计算距离信息并将其传送到用户使用界面上。

在编程中，单独设置3个完成标志位State2_Ready、State3_Ready和 State4_Ready。当且仅当全部六路测距单元都完成初始化的工作之后，State2_Ready变为低电平，State3_Ready处于高电平状态，用于触发State3工作;当且仅当全部六路测距单元都完成发送各自脉冲编码数字调制激励序列的工作之后，State4_Ready处于高电平状态，用于触发State4工作。以此来保证FPGA内部工作正常、有序地执行。

系统具体的工作流程如下:

程序编译成功之后，将程序下载到FPGA芯片中(芯片选用的是Altera公司的EP2C35F484C8)，系统自动进入初始化环节。FPGA中的管脚Sign_Control输出高电平，开关控制电路接收到高电平控制信号，则控制发射/接收一体电路处于超声波发射状态。这时，FPGA中的管脚Sign_Transmit输出脉冲编码数字调制激励序列，超声换能器开始发射超声波。超声波发射结束后，FPGA中的管脚Sign_Control输出低电平，开关控制电路接到这个低电平控制信号后，将控制发射/接收一体电路处于回声接收状态，等待回波信号的到来。

超声换能器接收回声信号后，通过信号调理电路的处理，从而得到数字信号。这个信号通过管脚InData进入回波识别模块进行匹配处理。基于相关判别法判断本地码与接收的回波信号是否相关，从而确定回波信号是否为自身回波。这种方法也称为回波识别算法，具体步骤为:

第1步 将回波信号送入FPGA的移位寄存器中;

第2步 将回波信号与预存在ROM中的本地码进行过零极化相关运算;

第3步 将此计算结果与预设的阈值比较。如果计算结果大于阈值，那么说明此回波信号为自身换能器发射超声波的回波;否则，不是自身回波。其中阈值的选取是通过大量的实验研究而得到的。

第4步 捕获相关运算峰值对应的时间点，计算渡越时间，得出距离值。

在系统计算距离信息的同时，还将已得到的距离信息通过RS-232接口，传输到上位机，在用户使用界面显示。这样用户可以在使用界面上实时地得到距离信息。图5给出了FPGA的工作流程图。

当以上内容完成后，系统会自动进入State3状态，继续发射超声波，一直循环下去。如果外部系统指示信号突然变为无效，或者由于不可预测的原因状态机转入了不确定状态，那么FPGA系统会在内部时钟的下一时刻到来后，自动进入State1状态。这样设计可以使系统工作更为稳定，容错性更好。

图5 FPGA工作流程图

3 实验结果与分析

图6给出了本文设计的六路无串扰超声测距仪原型样机图。基于此原型样机，开展了无串扰及有串扰两种情况下的测距实验。

图6 六路无串扰超声测距仪原型样机

3.1 无串扰情况下超声测距实验结果

当六路超声测距系统的各个测距单元相互独立时，如图7所示，即测距时只有一路超声测距单元向障碍物发射超声波。图7中障碍物采用的是表面平整光滑的有机玻璃，对声音的反射能力强。

图7 超声换能器与障碍物相对位置图

实验的具体实施方法如下:超声换能器发射面始终垂直于障碍物，然后不断改变障碍物与超声换能器之间的距离，并从用户使用界面上读取每次距离变化后的数据结果。由于六路测距数据量较大，我们在这里取的是六路测距结果的平均值，如图8所示;测距结果的绝对误差和相对误差如图9所示。

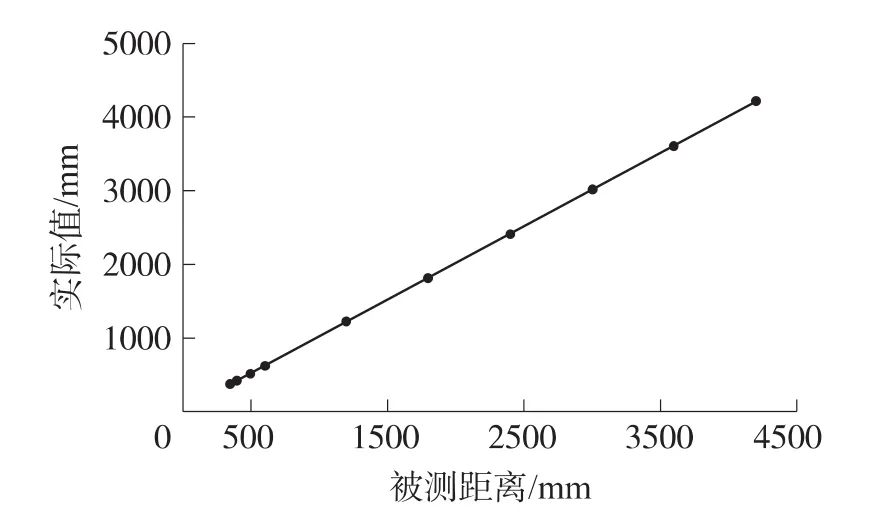
图8 实际值与被测距离的关系图(无串扰)

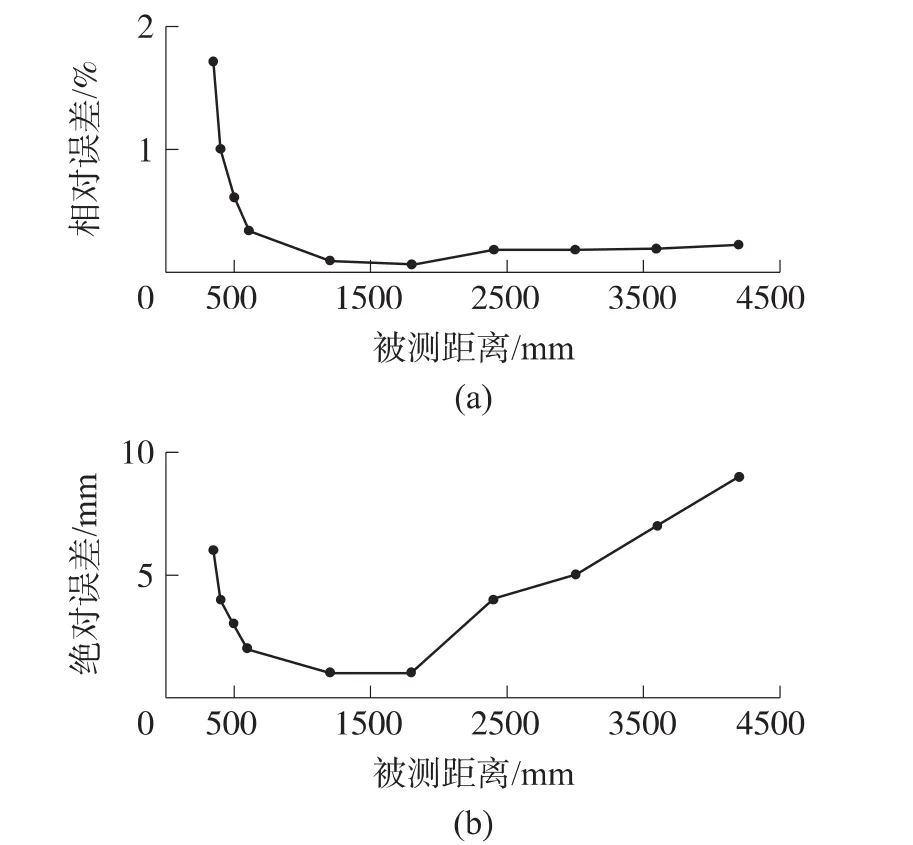
图9 误差与被测距离的关系图(无串扰)

从图8和图9中可以看出，在相互独立的超声测距实验中，测量的范围为350 mm～4200 mm，测量的绝对误差小于10 mm，相对误差在2%之内。当距离在350 mm～500 mm之间，由于接近超声换能器的测量盲区，测量的误差反而比距离在500 mm～2 000 mm的误差大。距离在500 mm～3 000 mm之内的测量精度很高，在测量距离超过2500 mm后，测量误差随着距离的增加而增加。这说明本文的超声测距系统的最佳测量范围是500 mm到3 000 mm之间，能够满足移动机器人避障需要。

3.2 有串扰情况下超声测距实验结果

本文中产生串扰的方法是目前发生串扰现象中最极端的一种方式:将六路超声测距单元分为3组，每组由2路超声测距单元组成。在每组实验中，将2个超声换能器相对放置，固定其中一个超声换能器，而移动另外一个，并且在移动过程中始终保持2个换能器之间位置不变且中心在同一个水平面内，如图10所示。3组测距结果的平均值如图11所示，测距结果的绝对误差和相对误差如图12所示。

从图11和图12中可以看出，在相互串扰的超声测距实验中，测量的绝对误差小于10 mm，相对误差在2.5%之内。通过图11、图12与图8、图9对比，可以发现在有串扰发生的情况下测距结果与无串扰情况的结果几乎相同。这说明本测距系统能很好保证测距时候不受串扰信号的干扰。

图10 同组超声换能器之间相对位置图

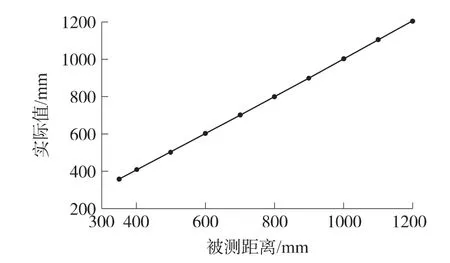
图11 实际值与被测距离的关系图(有串扰)

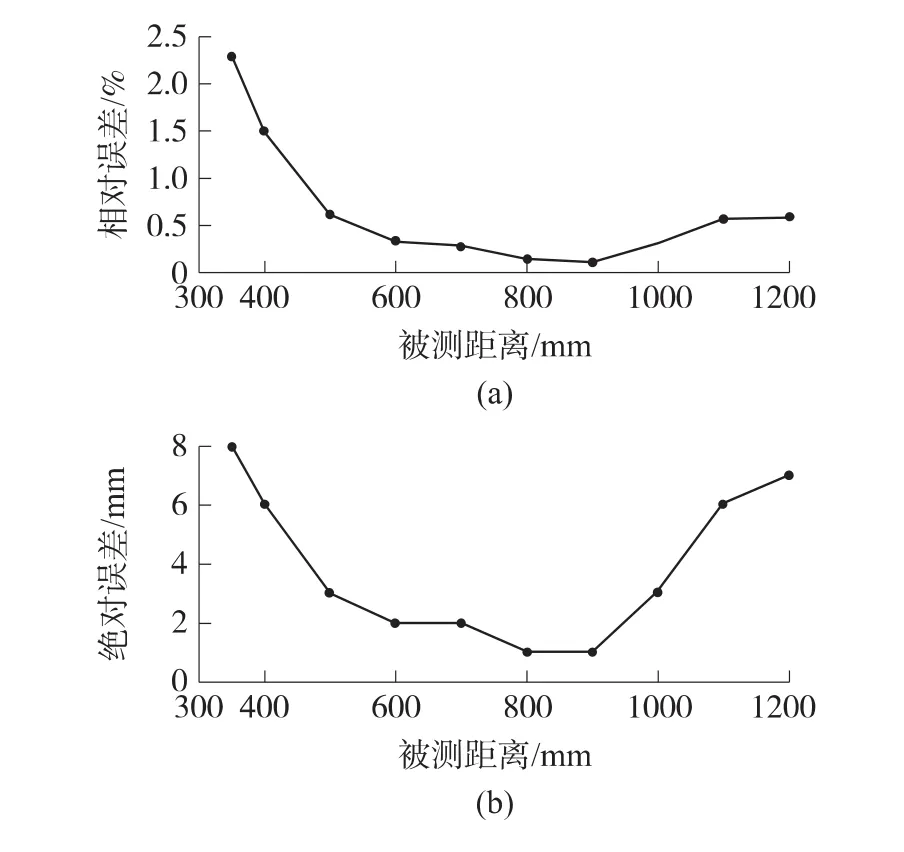
图12 误差与被测距离的关系图(有串扰)

另外，在以上两组实验中，测距系统发射激励信号需要2 ms。当测量最远距离420 cm时，超声波从发射到返回超声换能器需要大约25 ms(其中假设声速为340 m/s);从回波信号进入FPGA中进行处理到得出正确距离信息值最多需要53 ms(根据FPGA内部时钟信号测算得出的结果)，所以从测距系统发射激励信号到得到距离信息值的最多需要80 ms。说明此测距系统具有很好的实时性，在距离改变之后马上能捕捉到新的距离信息值，能够辅助机器人导航、识别周围环境信息。综合以上两组数据的分析，说明本文的六路无串扰超声测距系统具有可行性和实用性。

4 结论

针对移动机器人超声测距系统中存在的测量精度低和串扰问题，本文在前期有关超声硬件电路设计及编码激励研究的基础上，给出了一个基于FPGA的六路无串扰超声测距系统的设计与实施方案，并研制了原型实验样机。基于原型样机，进行了无串扰及有串扰两种情况的测距实验，结果表明即使在串扰发生的情况下，所设计的测距系统也可在35 cm～420 cm的范围内实现10 mm的测距精度。本文所设计的系统可用于多个超声换能器同时工作的场合，在满足测距精度的前提下可有效提高工作效率。

致谢

此课题从立项到结题历时8年，期间多位硕士生及博士生参与了此课题的研究并做出了自己的贡献，他们是张跃、梁琼、姚凤娟、郝强、兰少莹、李根旺、彭涵阳、姚振静、宋宇龙、杨雪、张姣姣，在此一并表示感谢。

［1］ Jörg K W，Berg M.Sophisticated Mobile Robot Sonar Sensing with Pseudo-Random Codes［J］.Robotics and Autonomous Systems，1998，25(3-4):241-251.

［2］ Parrilla M，Anaya J，Frisch C.Digital Signal Processing Techniques for High Accuracy Ultrasonic Range Measurements［J］.IEEE Transactions on Instrumentation and Measurement，1991，40(4):759-763.

［3］ Huang S S，Huang C F，Huang K N，et al.A High Accuracy Ultrasonic Distance Measurement System Using Binary Frequency Shift-Keyed Signal and Phase Detection［J］.Review of Scientific Instruments，2002，73(10):3671-3677.

［4］ 姚振静.超声扩频测距脉冲编码激励与渡越时间估计［D］.天津:天津大学电气与自动化工程学院，2010.

［5］ Yao Z J，Meng Q H，Zeng M.Improvement in the Accuracy of Estimating the Time of Flight in an Ultrasonic Ranging System Using Multiple Square-Root Unscented Kalman Filters［J］.Review of Scientific Instruments，2010，81(10):1-7.

［6］ 黄增荣，秦会斌，黄博志，等.超声测距中的伪随机码渡越时间的捕获［J］.传感技术学报，2006，19(3):843-846.

［7］ 葛万成，吴凤萍.两步相关法高抗干扰超声波距离测量技术的研究［J］.仪器仪表学报，2002，23(3):253-256.

［8］ 潘仲明，简盈，王跃科.基于两步相关法的大量程超声波测距技术.电子测量与仪器学报，2006，20(5):73-76.

［9］ 林圃.无串扰超声测距系统硬件电路设计与建模［D］.天津:天津大学电气与自动化工程学院，2008.

［10］李根旺.无串扰超声测距系统硬件设计与激励方法［D］.天津:天津大学电气与自动化工程学院，2009.

［11］彭涵阳.无串扰超声测距系统的激励方法及基于FPGA的设计与实现［D］.天津:天津大学电气与自动化工程学院，2010.

［12］ Fortuna L，Frasca M，Rizzo A.Chaotic Pulse Position Modulation to Improve the Efficiency of Sonar Sensors［J］.IEEE Transactions on Instrumentation and Measurement，2003，52(6):1809-1814.

［13］ Ure˜n J，Mazo M，García J J，et al.Correlation Detector Based on a FPGA for Ultrasonic Sensors［J］.Microprocessors and Microsystems，1999，23(1):25-33.

［14］ Hernández A，Ure˜na J，GARCíA J J.Ultrasonic Ranging Sensor Using Simultaneous Emissions from Different Transducers［J］.IEEE Transactions on Ultrasonic，Ferroelectrics and Frequency Control，2004，51(12):1660-1670.

［15］ Nakahira K，Kodama T，Furuhashi T，et al.Design of Digital Polarity Correlators in a Multiple-User Sonar Ranging System［J］.IEEE Transactions on Instrumentation and Measurement，2005，54(1):305-310.

［16］程晓畅，苏绍景，王跃科，等.伪随机码超声扩频测距系统设计与算法［J］.测试技术学报，2007，21(1):79-83.

［17］杨斌虎.伪随机序列相关的超声波测距系统研究［D］.太原:太原理工大学，2004.

［18］孟庆浩，兰少莹，姚振静，等.优化伪随机脉冲位置调制序列激励的无串扰超声测距系统［J］.传感技术学报，2008，21(9):1645-1649.

［19］ Meng Q H，Lan S Y，Yao Z J，et al.Real-Time Noncrosstalk Sonar System by Short Optimized Pulse Position Modulation Sequences［J］.IEEE Transactions on Instrumentation and Measurement，2009，58(10):3442-3449.

［20］杨雪.脉冲编码激励超声扩频测距系统性能分析［D］.天津:天津大学电气与自动化工程学院，2011.