阶梯波调制的H桥级联逆变器积分复位控制

汪渊

(重庆大学电气工程学院，重庆 400044)

1 引言

级联型逆变器与二极管钳位型和飞跨电容型的逆变器相比，具有诸多优点。基于阶梯波合成的级联型多电平逆变器具有开关工作频率低、开关损耗小、波形逼近正弦波等优点。故它适合于波形质量要求高和开关损耗要求低的大功率场合。H桥级联型逆变器有多种控制方法，这些控制方法按调制方式可分为两类，一是阶梯波调制下的，二是脉冲宽度调制下的。在阶梯波调制方式下，具体的控制方法有指定谐波消除法、多载波调制法、低次谐波含量最少法。在脉冲宽度调制方式下，具体的控制方法主要有相移SPWM法、多载波SPWM法等。本文研究的主要是阶梯波调制方式下的具体控制方法。虽然阶梯波调制具有上述优点，但阶梯波调制方式下现有的具体控制方法存在缺陷，即需要求解高阶非线性方程组，随着逆变器的H桥数增加，方程组的复杂程度也急剧增加，计算耗时长，故它在H桥数较多(5H桥以上)的逆变器中难以应用。

针对上述缺陷，本文提出一种不需要求解高阶非线性方程组的积分复位控制方法。其优点是在阶梯波调制方式下可以实现对H桥数较多的逆变器的控制。

2 积分复位控制方法

该方法基于面积等效原理，通过对输出波形积分值与参考波形积分值的比较来决定开关时刻，进而决定输出的阶梯波。这一控制方法的研究分三个方面，包括电路与工作波形、积分复位控制策略、仿真分析。

2.1 H桥级联型逆变器拓扑与阶梯波调制方式下的输出波形

图1为串联连接的H桥级联型逆变器拓扑示意图。每个H桥单元自带直流电源Ud，每个H桥单元都有Ud，0，－Ud三种输出电平，通过串联连接后，各个H桥输出电平可以互相叠加。若每个H桥单元直流电压值都相等，则逆变器输出电平数为2N+1(N为级联单元数)。在阶梯波调制方式下，各个H桥输出电平叠加形成阶梯波。

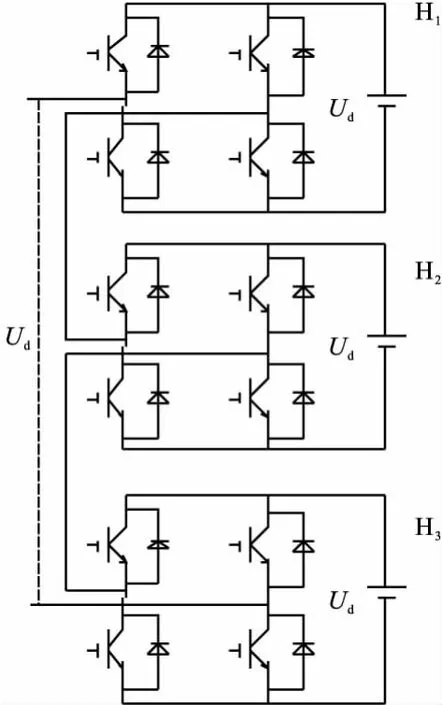
图1 H桥级联型逆变器拓扑

图2为H桥级联型逆变器输出阶梯波形示意图。控制各个H桥单元的开关时刻，可以使得合成的阶梯波逼近正弦波。

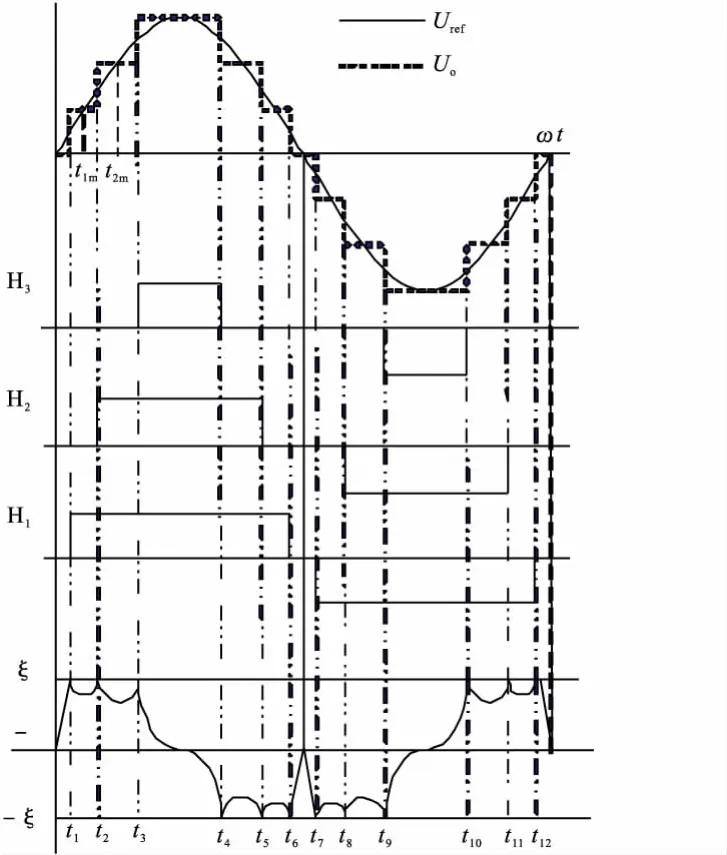
图2 阶梯波调制方式下的输出波形

2.2 H桥级联逆变器的积分复位控制策略

以图1所示3个H桥单元级联的H桥级联型逆变电路为例，说明积分复位控制的控制策略。

设参考信号Uref=Umsin(ωt)，三个H桥单元的直流电压均为Ud=Um/3。这样，逆变器的输出电压共有7 种电平，分别为 3Ud，2Ud，Ud，0，－Ud，－2Ud，－3Ud。

定义参考波形Uref的积分与输出波形Uo的积分之差为 Δ，Δ=∫Urefdt－ ∫U0dt。定义控制参数 ξ，当Δ≥ξ时，控制某一个H桥的导通或者关断使输出电压Uo上升一个台阶;当Δ≤－ξ时，控制某一个H桥的关断或者导通使输出电压Uo下降一个台阶。

图2所示的整个周期内所有的开关时刻的开关动作与输出波形的变化情况，可整理为表1。

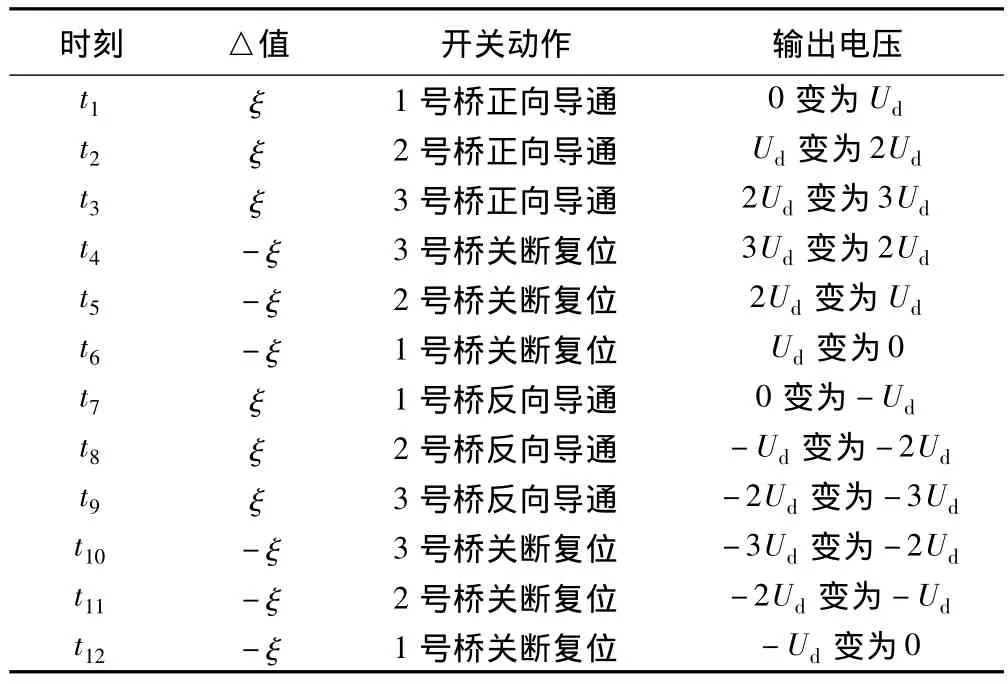
表1 一个周期内所有开关时刻的开关动作

图2所示，在零时刻，Uo=0;在t1时刻，Δ值达到上限ξ，控制电路发出信号使H1开通，逆变电路总的输出波形上升一个台阶，为Uo=Ud;在t2时刻，Δ值再次达到上限ξ，控制电路发出信号使H2开通，总输出波形再上升一个台阶，Uo=2Ud;t3时刻同理。

在t4时刻，Δ值达到下限－ξ，控制电路发出信号使H3关断，即H3输出电平复位到0，总输出波形下降一个台阶;t5时刻、t6时刻同理。

t7、t8、t9时刻，H 桥依次反向导通，总输出波形继续下降。t10、t11、t12时刻，H桥依次关断复位，总输出波形上升。

这样，通过对Δ值与ξ值的大小关系的判断，来决定开关时刻，使得逆变器输出电压波形呈阶梯波形。

2.3 控制参数取值范围

控制参数ξ必须满足一定的取值范围。如图2所示，在0＜t＜t1m这段时间内，必有一个H桥开通，否则不能合成阶梯波形。故ξ的取值必须满足

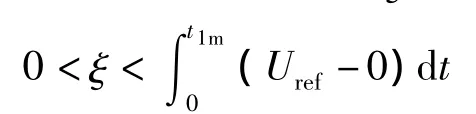
同理在t1m＜t＜t2m时间段内，ξ的取值必须满足

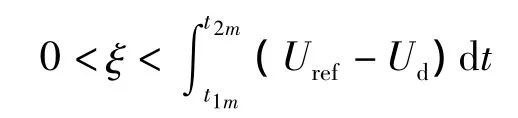
以此类推，对于具有N个H桥的级联逆变器，若参考信号Uref=Umsin(ωt)，每个H桥单元直流电压均为Ud=Um/N，则控制参数ξ的取值范围为:

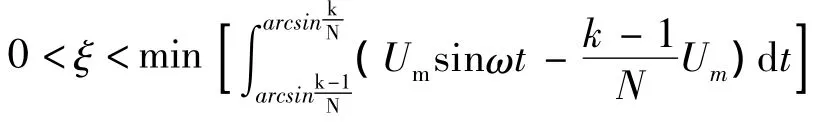
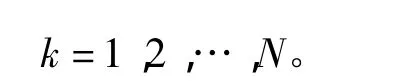
2.4 控制参数优化

图2(下图)所示设置的控制参数为常数，它可能会导致开关时刻分布不均和谐波含量偏大的问题出现。为解决这个问题，应设法对控制参数取值进行优化，使ξ随着参考波形的变化而变化。例如ξ=a+f(Uref)(a是常数，f(Uref)是关于参考波形Uref的函数)。在允许取值范围较大的区间上，ξ值相应扩大;在允许取值范围较小的区间上，ξ值相应缩小(如图3)。这样，可以使得逆变器的阶梯波输出能更好地跟踪参考信号。

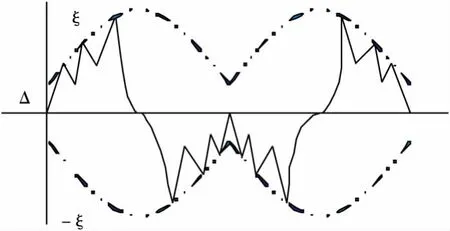
图3 优化示意图

3 仿真实验分析

应用Matlab软件包对积分复位控制方法进行仿真。

3.1 对3H桥级联逆变器的仿真分析

仿真设定为单相，直流电源电压均为100V，参考信号设为Uref=300sin(100πt)，负载条件为空载。控制参数 ξ=4.4655 ×10－2。

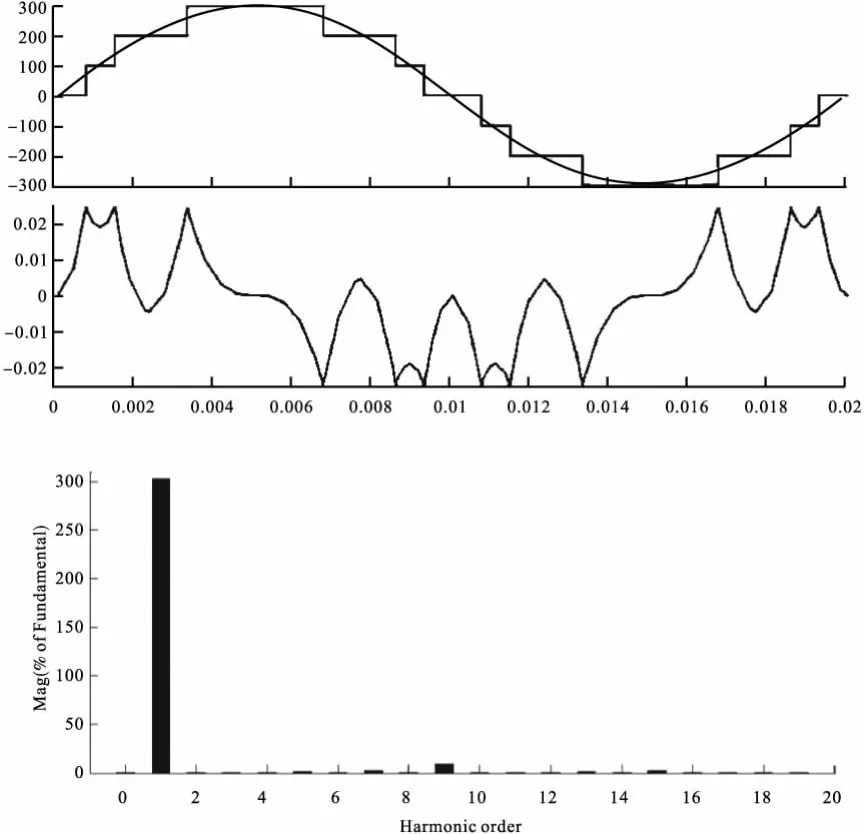
图4 3H桥级联逆变电路的仿真

图4中，上图显示输出阶梯波形，中图显示积分差值Δ，下图显示输出波形的频谱。对仿真结果进行Fourier分解，基波幅值为 303.5V，总谐波畸变率THD=13.85%。

ξ优化后，再次进行仿真:其他条件同上，控制参数设为ξ=0.01+0.0001|Uref|。

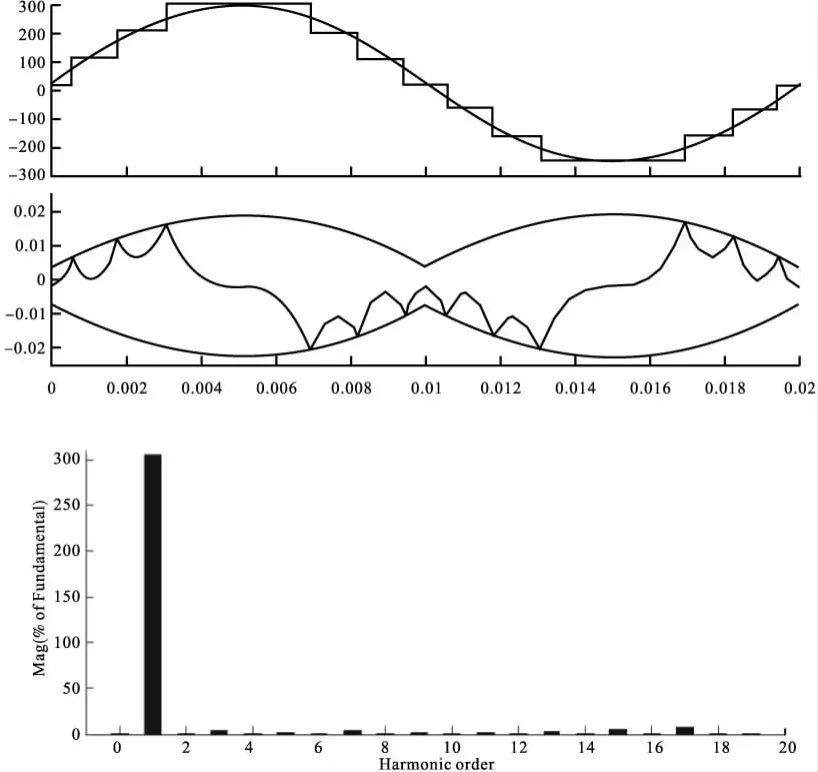
图5 优化后的仿真波形

仿真结果显示 THD=12.70%，基波幅值为304.8V。与图4对比可知，对于同一个3H桥电路，ξ优化后THD降低，这表明ξ优化使阶梯波形更逼近正弦波。

3.2 对5H桥和7H桥的仿真

下面对5H桥级联逆变电路进行仿真。参考信号设为Uref=100sin(100πt)，每个直流电源电压均为20V，控制参数设为 ξ=1.57×10－3+4×10－5|Uref|。

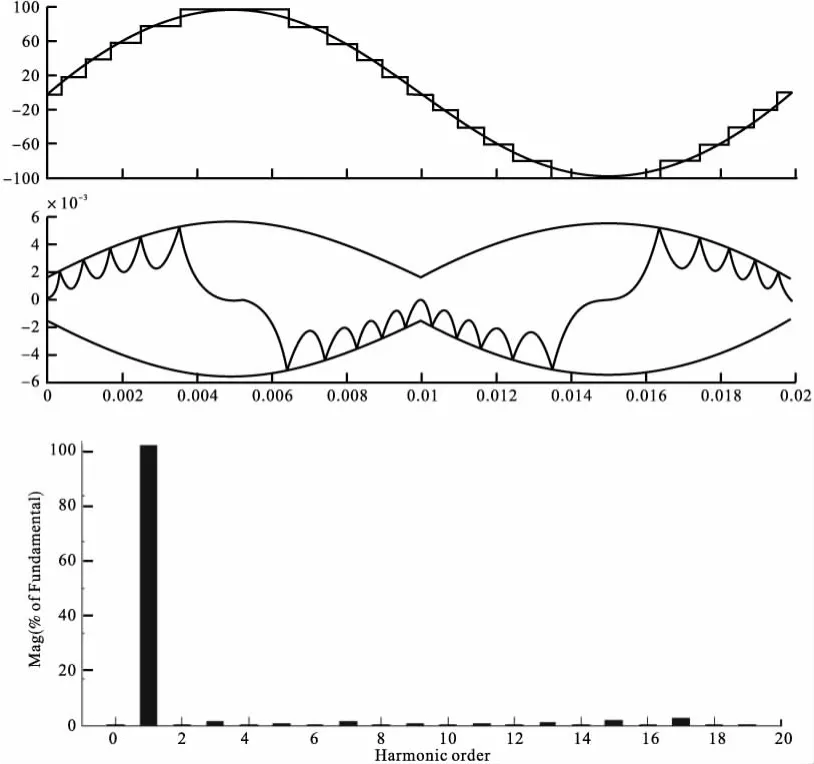
图6 5H桥级联逆变电路的仿真

5H桥级联逆变电路的仿真结果显示输出波形基波幅值为100.8V，THD=7.69%。

下面对7H桥级联逆变电路进行仿真。设参考信号Uref=140sin(100πt)，直流电压均为20V，控制参数设置为 ξ=1.45×10－3+2×10－5|Uref|。

7H桥级联逆变电路的仿真结果显示基波幅值为140.6V，THD=5.54%。

通过对5H桥和7H桥级联逆变电路的仿真，证明积分复位控制可以应用在电平数更多的级联逆变电路上。理论上，即使级联逆变电路的H桥数继续增加，此控制方法仍然可以应用。

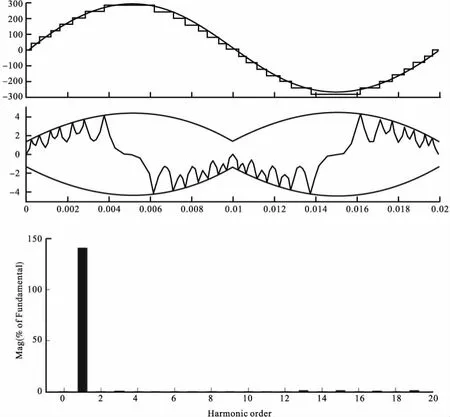
图7 7H桥仿真结果

4 结语

积分复位控制方法通过对输出波形积分值的控制，使其跟踪参考信号积分值，并由此计算开关时刻，与指定谐波消除法相比，其优势在于，它无需求解高阶非线性方程组。理论上，由于积分复位控制方法仅需对积分差值与上、下限值进行比较，无需复杂的计算，所以，即使逆变器多电平数更多，其控制过程耗时仍然较短，能在电平数更多的逆变器中应用。

在硬件实现方面，积分复位控制不需要大容量存储器，可以大大简化控制装置，具有应用价值。

积分复位控制的级联式逆变器，在生产实践中可用于分布式电源等场合。

在有关控制参数的优化上还可以进一步研究，例如在不同的区间上采用分段取值的办法，最终使得输出波形更加逼近正弦波形。

［1］ Lai J S，Peng F Z.Multilevel converters a new breed of power converters［J］.IEEE Trans.on Industry Applications，1996，32(3):509 －517.

［2］ Rodriguez J，Lai J S，Peng F Z.Multilevel converters:A survey of topologies，controls，and applications［J］.IEEE Trans.On Industrial Electronics，2002，49(4):724 －738.

［3］ Tolbert L M，Chiasson J N，Du Zhong，et al.Eliminating of harmonics in a multilevel converter with nonequal DC sources［J］.IEEE Trans.on Industry Applications，2005，41(1):75 －82.

［4］ 江友华，曹以龙.级联型多电平变频器不同阶梯波调制算法的谐波分析［J］.上海电力学院学报，2008，24(4):369 －374.

［5］ 张允.面积等效原理的新型多电平变换器控制算法［J］.电气传动，2005，35(1):19 －43.

［6］ 陈元娣.阶梯波调制级联逆变器触发角的一种简便算法［J］.电工电能新技术，2010，29(1):35 －40.