影响三轨法D－InSAR形变测量的相位测量误差定量分析

胡 剑，胡 艳

（北京卫星导航中心，北京100094）

0 引 言

合成孔径雷达差分干涉（D－InSAR）技术是在合成孔径雷达干涉（InSAR）技术的基础上发展起来的，采用地表发生形变前后的两幅SAR影像进行干涉处理，所获取的相位图中包含了地形信息和形变信息，利用一定的方法去掉相位图中的地形信息就可以得到形变信息［1］。同传统的测量方法相比，D－InSAR具有全天候、低成本和高空间分辨率等优势［2］，因而引起了学者们的高度关注。该技术不但为地球物理学和测量学工作者提供了监测多种地表形变的有效手段，而且在其他领域也有着广阔的使用前景［3］。

三轨法D－InSAR是D－InSAR技术的重要组成部分，它不需要外部数字高程模型（DEM）去除地形相位信息而获得形变信息，这是它的优势之一。三轨法D－InSAR比较适合植被稀少、气候干燥的地区所发生的形变监测［4］。三轨法D－InSAR形变测量过程，会受到雷达卫星参数、地形因素、平台姿态、基线等诸多因素的影响，最终会使三轨法形变测量精度产生较大的误差。在实际的地表沉降监测中，测量精度需要达到厘米甚至毫米量级，然而在三轨法D－InSAR数据处理中总会因为人为或者非人为的因素引入一定的误差，这些误差往往是客观存在的。因此，影响三轨法D－InSAR形变测量精度的误差就成为了关注的主要问题之一。虽然影响三轨法D－InSAR的误差来源是多方面的，但是相位误差、基线误差和地形因素是其中比较重要的三个方面［5］，对监测形变精度的影响比较大。因此，本文主要关注相位误差对三轨法D－In－SAR形变测量的影响。首先分析了三轨法D－In－SAR基本原理和数据处理流程，然后给出相位误差的模型，并分析讨论其影响。

1 三轨法D－InSAR的原理及数据处理流程

1.1 三轨法D－InSAR原理

三轨法D－InSAR就是利用三景雷达影像，其中的一幅在形变发生前获取作为主图像，分别与其他两景雷达影像进行干涉处理生成两幅干涉图，一幅包含地形信息，另一幅包含形变信息，去除平地效应后，分别实施相位解缠，最后采用差分干涉测量原理，经过计算就可以得到形变信息。图1是三轨法D－InSAR成像几何示意图。如果S1和S3是在地表发生形变前分别获取的，S2是在地表形变后获取，视线向上的形变量为ΔRd.

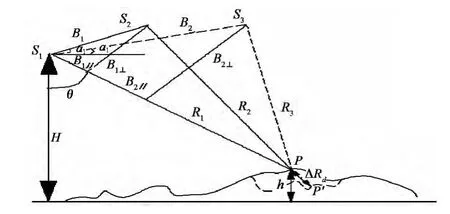
图1 三轨法D－InSAR几何原理图

天线S1和S2接收信号的相位为

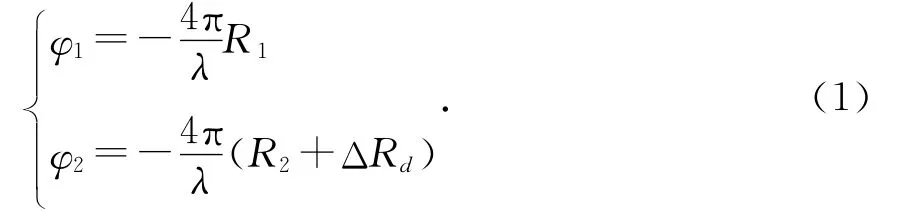
天线S1和S2进行干涉处理生成干涉图的相位为

式（2）中的干涉相位包含了地形信息和形变信息，因此，必须进行差分干涉处理去掉平地效应影响，才能获取形变信息。

天线接收信号的相位为天线S3和S1获取的雷达影像进行干涉处理生成的干涉相位为

由式（2）和式（4）可以得到，视线向形变量ΔRd所造成的相位为

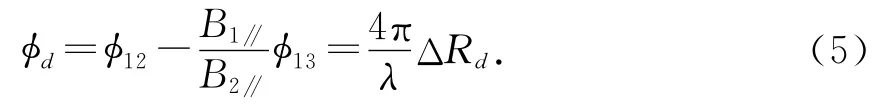
由式（5）可得：

式（6）中右边的各量，可以从干涉纹图的相位和轨道参数通过计算得到，进而可确定雷达影像每一点的视线向形变量ΔRd.

为了确保计算结果的精度和计算方便，可以使用“去平地效应”方法［6］来计算形变量ΔRd.

为了便于讨论问题，式（7）可以变为

式中：Δρ和式（7）中的ΔRd含义是相同的；φ′flat是去平地效应后含有形变和地形信息的干涉相位，φflat是去平地效应后含有地形信息的干涉相位；B′⊥和B⊥分别是形变干涉对和地形干涉对的有效基线。

1.2 三轨法D－InSAR数据处理流程

雷达卫星在对地面同一地物进行重复轨道观测时位置会发生瞬时变化［7］，因此，在数据处理时，首先要进行配准和重采样。干涉相位解缠应在去除平地效应和滤波去噪后进行，这样可以对干涉相位的噪声信息进一步抑制。图2示出了三轨法基本处理流程。

图2 三轨法D－InSAR数据处理流程

2 相位测量误差模型及其分析

如果形变干涉对和地形干涉对的有效基线十分精确，此时对式（8）求全微分得

三轨法差分干涉测量，一般要求三幅雷达影像。假设这三幅是独立获取，分别为L0，L1，L2其中影像L0和影像L2是地表发生形变前获取，影像L1是地表发生形变后获取，并且这三幅雷达影像相位分别表示为φ0，φ1，φ2，其相位中误差分别为δ0，δ1，δ2.如果形变干涉纹图由L0和影像L1干涉处理生成，地形干涉纹图由影像L0和L2影像干涉处理生成，则形变干涉图和地形干涉图的相位可表示为

由式（10）得

由式（11）可推得三轨法差分干涉测量相位的协方差矩阵为

假设三轨法形变测量所使用的三幅雷达影像的相位中误差都是相同的，则由这三幅雷达影像进行干涉处理生成的形变干涉纹图和地形干涉纹图的相位中误差也是相同的，均为单幅雷达影像相位中误差的倍［8］，记作δφ：

由式（9）、式（12）、式（13）及协方差传播定律得

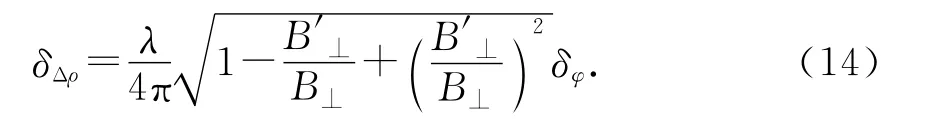
从式（14）可以看出，三轨法形变测量结果精度与相位误差和基线比有关。相位误差对三轨法形变测量影响的大小受到基线比的制约。相位误差对三轨法D－InSAR形变测量的体现在干涉纹图条纹变化情况。图3示出了模拟的当基线比发生变化时，干涉纹图条纹变化情况。图3表明，当基线比大于1时，干涉图上的条纹最稠密，这对相位解缠带来很大影响，甚至会造成相位解缠无法进行［9］，从而会引起数据处理结果准确性大幅度下降，地表形变结果情况也不能被准确反映出来；当基线比＝0.5时，此时干涉纹图条纹最为清晰，相位解缠也是非常容易进行的，得到的结果也是比较准确的，但是，基线比＝0.5的情况在实际三轨法形变测量中是非常少见的；当基线比＜1时，干涉条纹图的条纹虽然比较多，但是还是清晰可见的，也可以比较好的去除平地效应的影响。

图3 基线比变化对干涉图条纹的影响 （a）基线比＞1；（b）基线比＝0.5；（c）基线比＜1

在相位误差稳定时，基线比大小变化对三轨法D－InSAR形变测量影响也是比较明显的。图4示出了基线比大小变化对三轨法D－InSAR形变测量的影响。

从图4可以看出，随着基线比的增大，三轨法D－InSAR形变测量变化较大；反之，三轨法D－In－SAR形变测量变化较小。

基线比大小取决于地形干涉对有效基线和形变干涉对有效基线的大小，而这些有效基线是卫星视角θ的函数，因此，卫星视角θ间接影响了基线比大小。

相位测量误差主要是由基线去相关、时间去相关、多视数、像元失配准、斑点噪声和系统噪声存在而产生［10－11］。其中，系统噪声在星载SAR系统中是不可避免的，这与星载SAR卫星的研制有关；斑点噪声和衰落噪声总是会对三轨法D－InSAR干涉纹图中的每一个像元产生一定的影响，其可以通过多视平均法来减弱，这样就形成了多视数对三轨法D－InSAR形变测量的影响；三轨法D－InSAR干涉图中的相位反映的是同一地物之间的相位差，如果像元的配准出现偏差，干涉图中的一些散射体成份会引起干涉图中相位的变化。

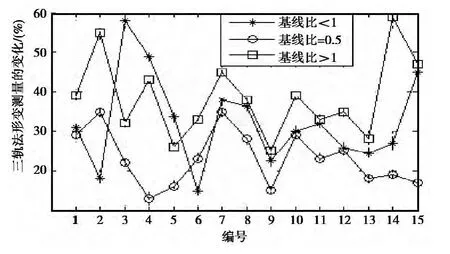
图4 基线比大小变化对三轨法D－InSAR形变测量的影响

3 结 论

由δΔρ表达式可知，基线比Ω是引起相位测量误差对三轨法形变测量造成影响的一个主要因素。基线比Ω主要取决于地形干涉对和形变干涉对的有效基线的大小，如果形变干涉对的有效基线大于地形干涉对有效基线，那么，将会使相位测量误差对三轨法形变测量产生较大的影响，此时干涉图的干涉条纹将会非常稠密，会对接下来的相位解缠造成很大困难，因此，在三轨法D－InSAR形变测量中，应当尽可能的利用较小有效基线的形变干涉对和较大有效基线的地形干涉对进行差分干涉处理，以达到尽可能较少相位测量误差对三轨法D－In－SAR形变测量的影响，从而使相位测量误差的影响较少到可以接受的程度。

基线比Ω和相位误差δφ都与卫星视角θ存在着一定的函数关系，而卫星视角θ和卫星观测的范围大小有很大关系，这也从一个方面反映了观测区域的大小也会是相位测量误差对三轨法D－InSAR形变测量造成影响的一个因素。因此，在三轨法形变测量中，星载SAR的视角θ也是必须要考虑的一个主要因素之一。

［1］ 王 超，张 红，刘 智.星载合成孔径雷达干涉测量［M］.北京：北京科学出版社，2002：59－63.

［2］ 陶秋香，刘国林，刘伟科.L和C波段雷达干涉数据矿区地面沉降监测能力分析［J］.地球物理学报，2012，55（11）：3681－3689.

［3］ 沈 强，乔学军，金银龙，等.ALOS PALSAR雷达影像InSAR数据处理中的基线和地形误差分析［J］.大地测量与地球动力学，2012，32（2）：1－6.

［4］ 王志勇，刘 磊，周兴东.利用合成孔径雷达差分干涉测量技术监测伊朗Bam地震同震形变场［J］.西北地震学报，2008，30（4）：310－316.

［5］ 刘国祥.InSAR系统中的误差传播［J］.四川测绘，2005，28（2）：92－95.

［6］ 程三友，刘少峰，申旭辉.差分干涉雷达测量在地面沉降中的应用研究［J］.东华理工学院学报，2004，27（4）：355－360.

［7］ 王志勇，张金芝.基于InSAR技术的滑坡灾害监测［J］.大地测量与地球动力学，2013，33（3）：87－91.

［8］ 余景波，刘国林，曹振坦，等.大气延迟误差对In－SAR数据处理影响的定量分析［J］.空间科学学报，2012，32（5）：720－729.

［9］ 刘国林，闫 满.顾及模型误差的卡尔曼滤波相位解缠［J］.测绘科学，2012，37（2）：170－172.

［10］ 刘国林，郝晓光，薛怀平，等.影响InSAR测高精度因素的相关性分析［J］.武汉大学学报·信息科学版，2007，32（1）：55－58.

［11］ 余景波，刘国林，王肖露.影响四轨法D－InSAR形变测量精度误差的相关性分析［J］.地震工程学报，2013，35（2）：296－301.