基于批次加权正则极限学习机的发酵过程软测量

姚景升，刘 飞

(江南大学轻工过程先进控制教育部重点实验室自动化研究所，江苏无锡214122)

由于发酵过程机理复杂、影响因素众多、高度非线性，并且当今没有有效的生物传感器，所以一些重要变量如产物质量浓度、菌体质量浓度等无法在线测量，严重影响了过程控制与优化。目前，解决这一问题的方法之一是软测量技术，因此建立预测性能良好的软测量模型具有重要意义。近年来，应用于生物发酵过程的软测量建模方法主要包括机理建模、回归分析建模、人工神经网络等。其中，神经网络建模方法成为近年来研究的热点［1］。但传统基于梯度下降法的神经网络迭代次数多、易陷入局部极小、参数选择敏感等问题一直得不到很好的解决，限制了它的应用。

极限学习机(ELM)是近年来提出的一种针对单隐层前馈神经网络(SLFNs)的学习算法［2］。该算法已经通过许多标准问题和实际应用验证，结果表明其极大提高了前馈神经网络的计算速度，并且避免了传统神经网络因梯度下降法产生的很多问题［3］。ELM在提出后得到了进一步的改进与扩展［4-6］，并广泛应用于目标识别［7］、癌症诊断［8］、生化过程［9］、电力负荷预测［10］等领域。但由于ELM是基于经验风险最小化原理，在训练过程中容易导致过拟合，泛化能力较差。文献［11］借鉴统计学习理论中的结构风险最小化原理，提出了正则极限学习机(RELM)，通过引入正则项有效提高了模型的泛化能力。

由于RELM具有较ELM更好的预测能力，考虑将其应用于发酵过程软测量建模中。在实施RELM建模时，每批训练样本的地位是平等的，而实际发酵过程中批次间不同的发酵初始条件会导致不同的变量变化轨迹，所以当选定某一批次发酵过程作为预测对象时，各批次样本对它的预测能力是有差异的。因此，在训练过程中可以通过区别对待各训练批次来提高学习精度。文中引入批次加权的概念，根据各训练批次初始条件与预测对象初始条件之间的相似度，结合文中提出的相似度量化函数得到各训练批次的惩罚权值，进而实施加权回归。另外，RELM本身存在超参数估计问题，文献［11］利用传统的交叉验证方法进行超参数的选择，实验复杂性高，计算代价大，是一种非常耗时的超参数选择方法。文中采用贝叶斯方法［12］对超参数进行自适应估计，降低计算代价与实验复杂性。最后以青霉素发酵过程为例，建立了基于批次加权RELM(BWRELM)的软测量模型，仿真结果表明所建模型具有良好的预测能力。

1 基于批次加权RELM的软测量模型

1.1 正则极限学习机

假设有n个不同的训练样本，集合可以表示为D={(Xi，Ti)∣i=1，2，…，n;Xi∈RM，Ti∈Rm}，其中Xi是M维输入样本，Ti是m维输出样本。根据结构风险最小化原理，为较好的权衡结构风险与经验风险，RELM通过引入超参数γ来调节两种风险的比例。则具有N个隐含层节点的RELM数学模型可表示为

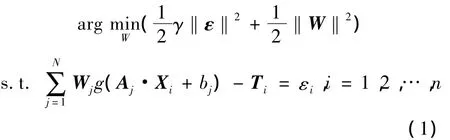
其中，Aj= ［aj1，aj2，…，ajM］T为输入层节点与第j个隐含层节点的连接权值，bj为第j个隐含层节点的阈值，Wj= ［wj1，wj2，…，wjm］T为第 j个隐含层节点与输出层节点的连接权值，Aj·Xj表示Aj与Xj的内积，g(·)为隐含层的激活函数，εi表示回归误差。

式(1)为条件极值问题，通过构造下面的拉格朗日方程转换为无条件极值问题:

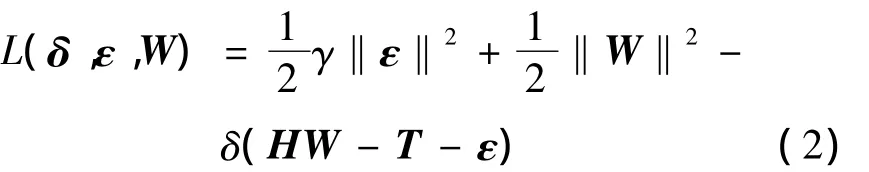
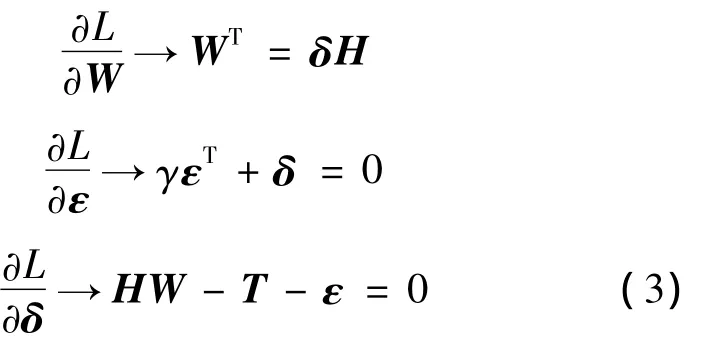
由式(3)求解得网络输出权值

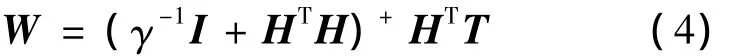
式中，I为单位矩阵。

1.2 批次加权回归

由发酵过程的实际情况以及实验研究发现，发酵初始条件对发酵过程有着十分重要的影响。初始条件相似的发酵过程，过程变量的变化轨迹相似，初始条件差别较大的发酵过程则会导致明显不同的变化轨迹，而且实际中各批发酵过程的初始条件的确存在差异。因此，为解决以上问题，文中引入批次加权概念并提出一种新相似度量化函数。

1.2.1 优化问题转换 为实现区别对待训练批次以达到提高模型预测精度的目的，可以采用加权的方法。这种方法根据一个评价标准，确定各样本在训练过程中的地位，分配不同的惩罚权值。此方法已经应用在一些算法的改进中。文献［13］利用加权的方法对ELM进行了改进，根据训练误差的大小来评价各个样本的重要程度，提高了模型的抗干扰能力和预测精度。文中结合发酵过程数据的批次特性，借鉴上述思想将目标由样本点变为批次，根据各训练批次在训练过程中的地位，给予不同的权值。具体实施方法是对RELM目标函数中的误差项进行加权，使得跟具体预测对象相似的训练批次在训练过程中获得更高的精度。假设有p个批次的训练样本，式(1)的优化问题可转换为

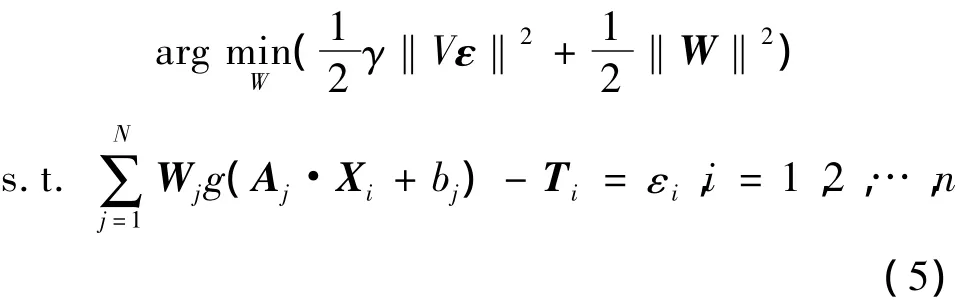
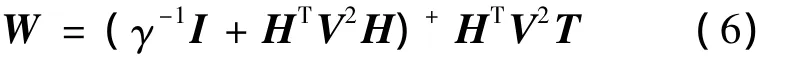
1.2.2 基于相似度的惩罚权值求解 文中采用各训练批次发酵初始条件与预测对象初始条件之间的相似度作为依据，通过相似度量化函数得到惩罚权值矩阵V。因此做出如下定义:对于第k个训练批次的初始条件与预测对象的初始条件ICk和IC，用两者之间的欧氏距离d(ICk，IC)来表示相似度，如下式:

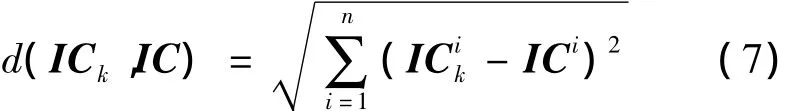
其中，n表示组成发酵过程初始条件的变量数目，为消除数量级不同带来的影响，将发酵初始条件进行归一化处理，使n个变量均限定在［0，1］区间内。

在计算出各训练批次与预测对象之间的相似度之后，采用如式(8)所示常用的相似度量化函数［14］对其进行量化得到可以用于度量各训练批次重要程度的惩罚权值vk:

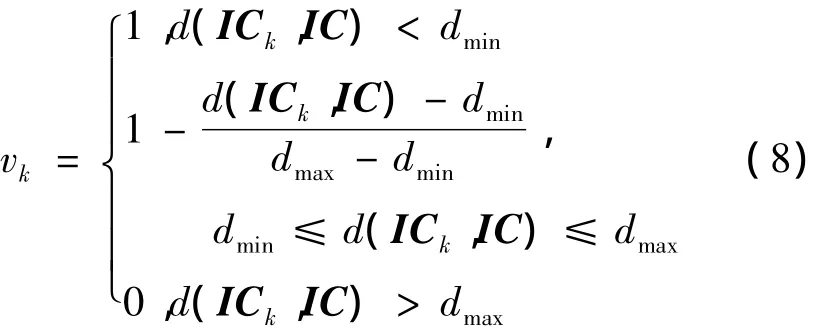
式中，dmax和dmin均为常数。

1.2.3 新相似度量化函数 观察式(8)，当相似度在dmin与dmax之间时，它是一个一阶函数，因此为了获得更高的预测精度，可以将函数前半段拉伸为凸函数，将函数后半段拉伸为凹函数。这样与预测对象相似的训练批次可以得到更大的权值，在训练过程中起到更大的作用。基于上述思想，文中设计了一种新相似度量化函数:

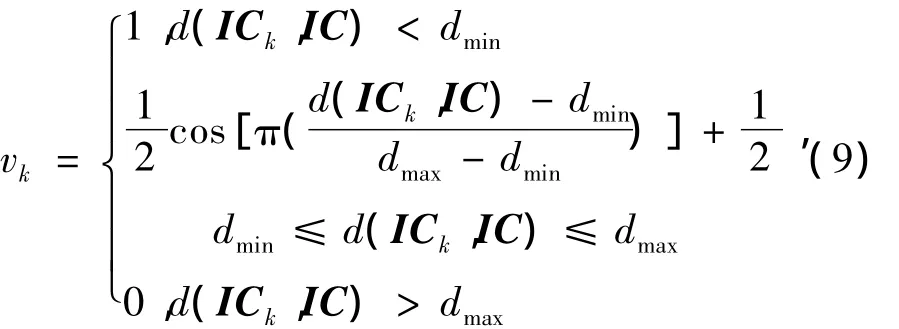
为了更直观比较上述两种相似度量化函数，令

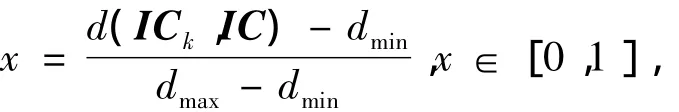
因此得到如下两式，并作图1。

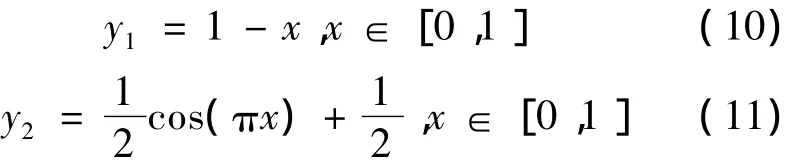
由图1可以很明显地看出，通过文中提出的新相似度量化函数计算得到的惩罚权值的惩罚力度更大，当某训练批次发酵初始条件与预测对象发酵初始条件之间的相似度接近dmin时，即图中x接近0时，新相似度量化函数相比常用函数可以赋予该训练批次更大的惩罚权值，进一步增强其在训练过程中的作用;相反，当某训练批次发酵初始条件与预测对象发酵初始条件的相似度接近dmax时，即图中x接近1时，新相似度量化函数赋予该批次更小的惩罚权值，进一步减弱其在训练过程中的影响。因此，从理论分析的角度，文中所提相似度量化函数可以更好地满足要求，建立的模型能够更好地对预测对象进行预测。

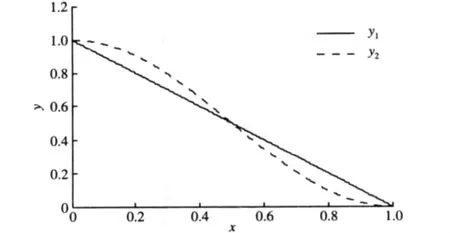
图1 y1与y2对比Fig.1 Contrast of y1 and y2

1.3 基于贝叶斯的超参数估计

正则化方法把避免网络学习过程的过拟合问题转化为对目标函数中起控制作用的超参数的估计问题。因此超参数选择的准确与否在一定意义上决定着正则化的有效性。传统的超参数估计方法是交叉验证法，计算量较大，且需要专门从数据集中分割出验证数据。贝叶斯参数估计是一种基于贝叶斯思想的有效参数估计方法，通过最大化网络输出权值与超参数的后验概率能够实现模型参数的自适应估计。

在给定样本数据D的情况下，由贝叶斯准则可得到权值后验概率为

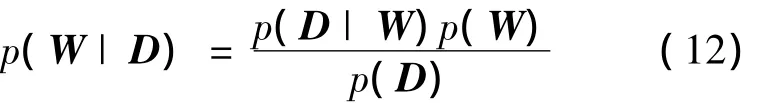
其中p(D)是归一化因子，与W无关，p(W)是权值的先验分布，p(D|W)是权值的似然函数。

假设目标数据由一个光滑的、具有加性零均值高斯噪声的函数生成且各数据独立同分布，权值先验满足高斯分布，则权值的先验分布为

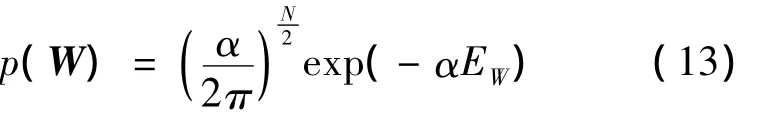
权值的似然函数为

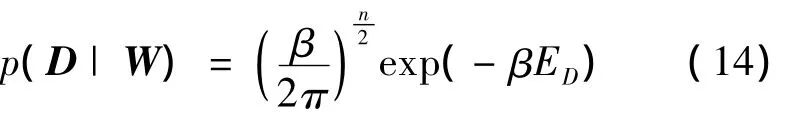
其中

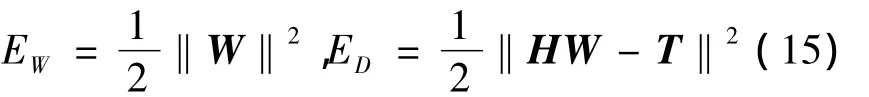
分别代表RELM中的结构风险与经验风险，超参数α与β对应两种风险的比例，控制对应分布的方差。则

权值的后验概率

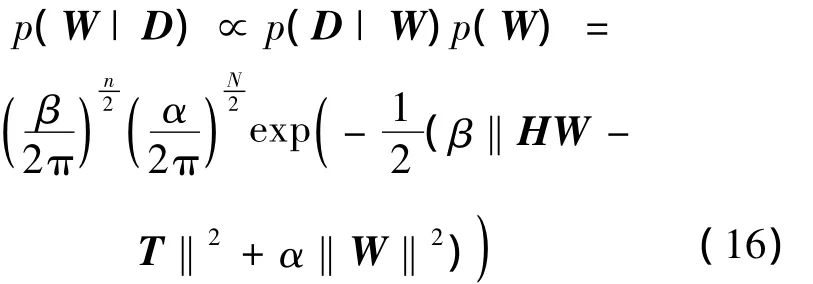
根据贝叶斯理论，最大化上式即能得到最优的权值，比较式(16)与式(1)可知，最大化权值的后验概率即最小化RELM的目标函数，式(1)中，γ=β/α。因此最大后验概率权值WMP即为上节求出的输出权值

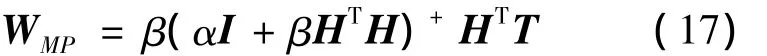
根据贝叶斯理论，同样可以通过最大化超参数的后验概率来得到最优超参数。利用贝叶斯准则，在给定样本数据D的情况下，超参数的后验概率为

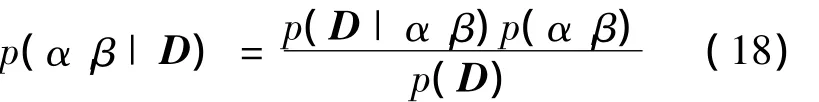
其中p(D)为归一化因子，p(α，β)与超参数无关;p(α，β)为超参数的先验概率，也称为超先验，这里假设其为一种很宽的分布函数(α与β在很大的范围内几乎不变);p(D|α，β)为超参数的似然函数，也称为α与β的置信度。因此超参数的后验概率可

通过最大化p(D|α，β)得到。

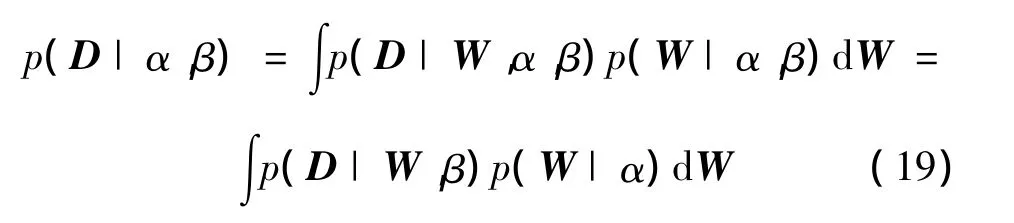
将式(13)和式(14)代入上式，并令S(W)=βED+αEW，可得

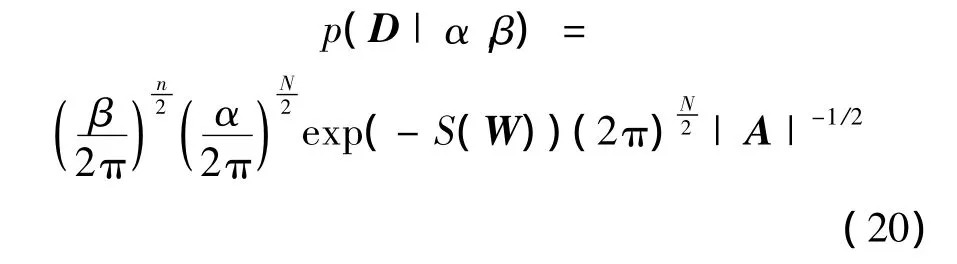
对上式取对数可得

其中，A=Λ+αI，Λ =β▽▽ED是误差平方和函数的Hessian矩阵。

对上式中α和β，分别求最大值，可得

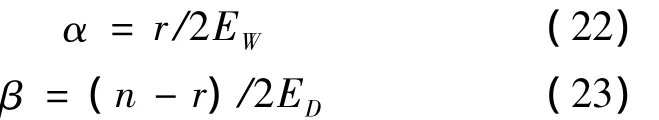
其中

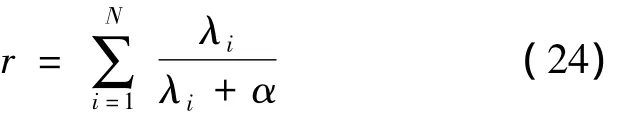
λi为Λ的特征值。

在实际应用中，需要找到α，β，WMP合适的值使概率最大，一种可行的方法是用迭代法求解WMP，并周期地更新α，β。

1.4 BWRELM算法步骤

1)网络初始化:给定隐含层激活函数g(·)，确定隐含层节点数，随机选取网络输入层与隐含层节点的连接权值Aj和阈值bj，初始化超参数α和β。

2)超参数迭代寻优:利用式(17)计算输出层最大后验概率权值W，分别利用式(15)和式(24)计算得到ED，EW，r，利用式(22)和式(23)更新超参数α和β，如果超参数α，β的变化量小于给定阈值，则说明收敛，超参数取现在的α与β，否则重复上述过程，直到满足条件或者达到最大迭代次数。

3)批次加权:对各训练批次与预测对象的发酵初始条件进行归一化处理，利用式(7)得到各训练批次发酵初始条件与预测对象发酵初始条件之间的相似度，利用式(9)实施对步骤2)中相似度的量化，得到各训练批次的权值vk，组成惩罚权值矩阵V，利用式(6)更新隐含层到输出层的权值W。

4)利用测试数据验证所建模型，通过设置均方根误差作为性能指标评价所建网络的预测性能，其计算公式如下:

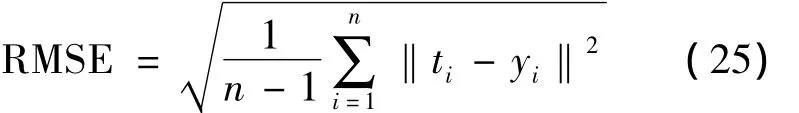
其中:n为数据的个数;ti为真实值;yi为模型预测值。

2 青霉素发酵过程仿真实验

仿真实验引用的数据来自美国Illinois州立理工学院Ali Cinar领导的过程监控与技术小组设计的青霉素生产仿真软件Pensim2.0。该软件的内核采用基于Bajpai机理模型改进的Birol模型，在此模型中，考虑了15种物理量及生物量对菌体质量浓度与产物质量浓度的影响，因此是一个能比较全面反映青霉素发酵实际过程的模型。通过此仿真软件，可以对不同操作条件下菌体质量浓度、产物质量浓度等多种变量进行仿真研究，因此可以作为后续建模、监测、优化和控制可靠的仿真实验平台，相关研究已表明该仿真平台的实用性与有效性［15］。

青霉素发酵是一类典型的生物发酵过程，具有时变性、高度非线性、不确定性等特点。发酵工艺过程是通过控制一系列工艺参数来实现的，其中，产物质量浓度等生物参数的实时测量对发酵过程的实时优化控制起着重要的作用。然而由于生物传感器的缺乏及发酵过程复杂的内在机理，这些生物参数的在线测量往往较为困难。因此建立这些关键变量的软测量模型对工业生产具有非常重要的意义。

在青霉素发酵生产过程中，部分变量如排气二氧化碳、溶解氧浓度等可以通过仪器直接进行测量，因此可以利用发酵过程中实时获取的参数建立预测产物质量浓度等不可测变量的软测量模型。文中建立产物质量浓度的软测量模型，因此主导变量为产物质量浓度。辅助变量通过分析各个变量与主导变量之间的相关关系得到，最终选择通风速率、底物流加速率、补料温度、溶解氧浓度、反应器体积、排气二氧化碳浓度、反应热以及碱流加速率8个变量。模型网络均为3层结构，输入层节点数为8个，隐含层激活函数为Sigmoid函数，隐含层节点数为40个，输出层节点数为1个。

结合对青霉素发酵过程的分析和在仿真平台上的实验研究，发酵初始条件由初始基质质量浓度(S0)、初始菌体质量浓度(X0)与初始pH值(pH0)组成，式(8)，(9)中两个参数的取值为:dmin=0.1，dmax=1.2。然后由仿真平台产生不同初始条件下的6批样本数据，发酵过程反应时间为400 h，采样时间为 1 h，选择初始条件［S0，X0，pH0］为［15.21，0.1，5.0］的批次作为预测样本，另外5批作为训练样本。分别用ELM，RELM，采用常用相似度量化函数的批次加权RELM(BWRELM0)与采用新相似度量化函数的批次加权RELM(BWRELM)对训练样本进行训练，建立了预测模型，它们的仿真预测结果分别如图2、图3、图4、图5所示。

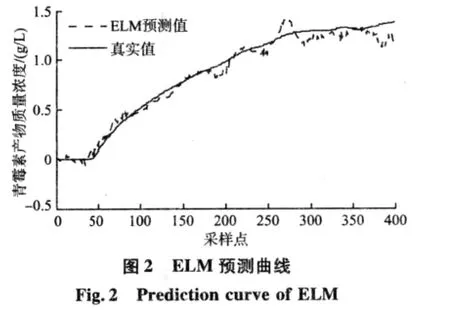
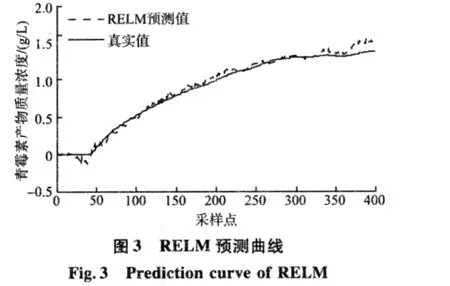
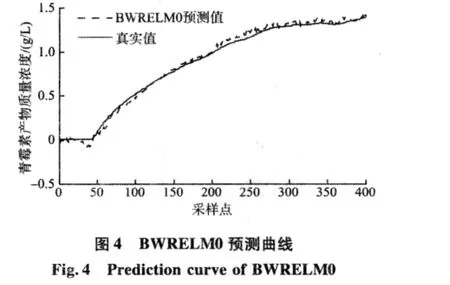
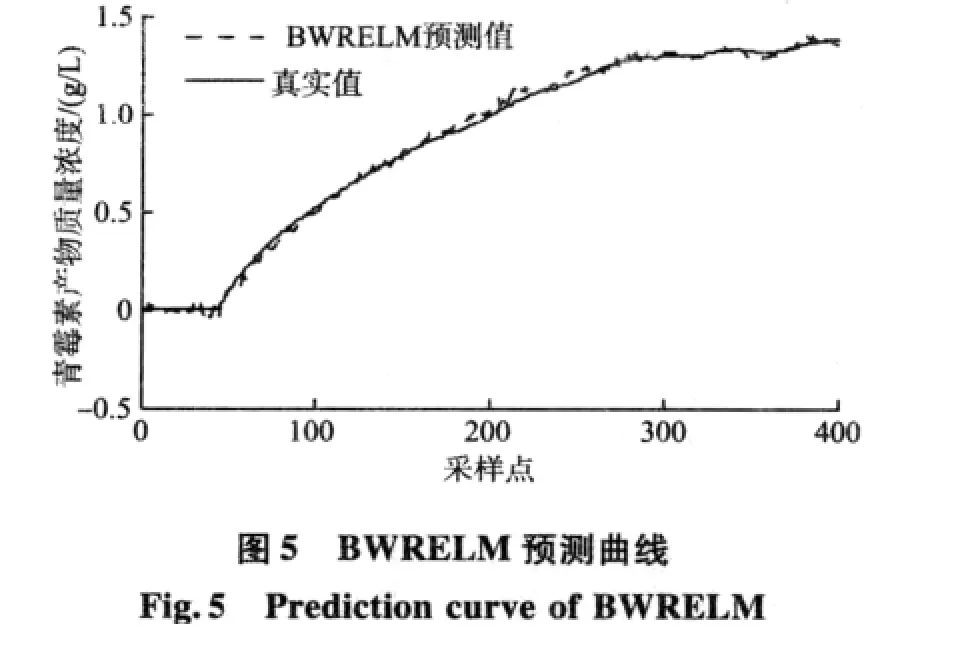
由图2和图3可以看出，ELM的预测效果较差，预测曲线有很大的起伏;RELM的预测效果比ELM好，预测曲线也更加平稳。这是因为RELM通过引入结构风险，提高了泛化能力。由图4和图5可以看出，两种基于批次加权RELM的预测效果好于未加权的。通过区分各训练批次的重要程度，达到了提高模型预测精度的目的。另外通过比较图4和图5可以看到，采用新相似度量化函数建立的模型比采用常用函数建立的模型预测精度更高，仿真结果与理论分析一致，说明文中提出的新相似度量化函数更好。同时，基于贝叶斯参数估计的3种算法良好的预测效果也说明了贝叶斯参数估计的有效性。

为了更好地比较4种方法，首先，表1给出了4种方法的训练误差、预测误差与训练时间。可以看出，RELM的训练误差与预测误差均比ELM小，训练时间上与ELM接近，保持了ELM的快速性;两种批次加权算法的训练误差和预测误差都比前两种算法小，其中采用新相似度量化函数的算法预测误差更是达到了0.024 3，接近ELM预测误差的1/3，预测效果最好。两种批次加权算法的训练时间因为计算惩罚权值的关系略长，但0.2 s的训练时间完全可以满足在线测量的实际要求。另外，表2、表3分别给出了两种算法各训练批次的发酵初始条件、惩罚权值以及对应的训练误差。由表2、表3可以看出，训练误差与各批次权值成反比，权值越大，学习精度越高，即该批训练样本在训练过程中的作用越大。另外，通过比较表2与表3的权值与训练误差可以看出，新相似度量化函数的惩罚力度更大，使得所建模型的预测精度更高。

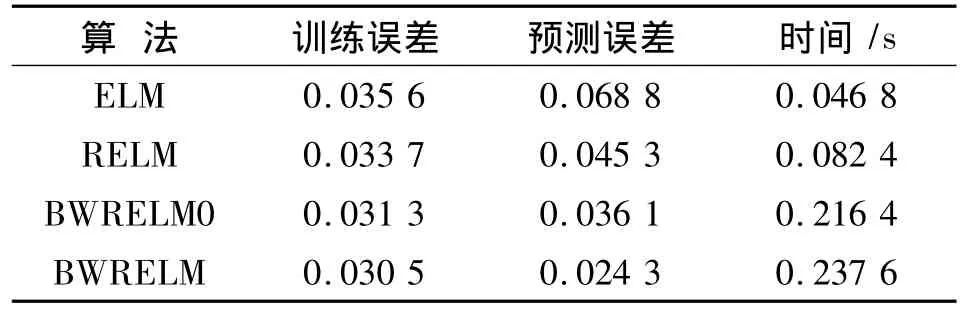
表1 4种算法的比较结果Tab.1 Comparison of 4 kinds of algorithms

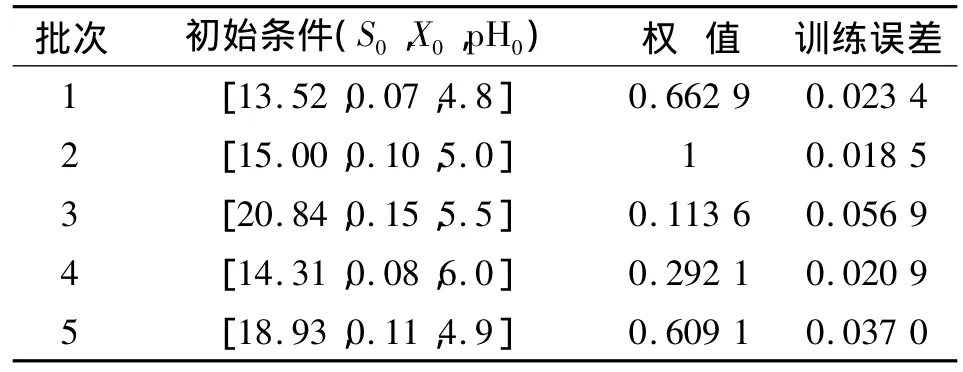
表2 BWRELM 0权值与训练误差Tab.2 Weights and training errors of BWRELM 0

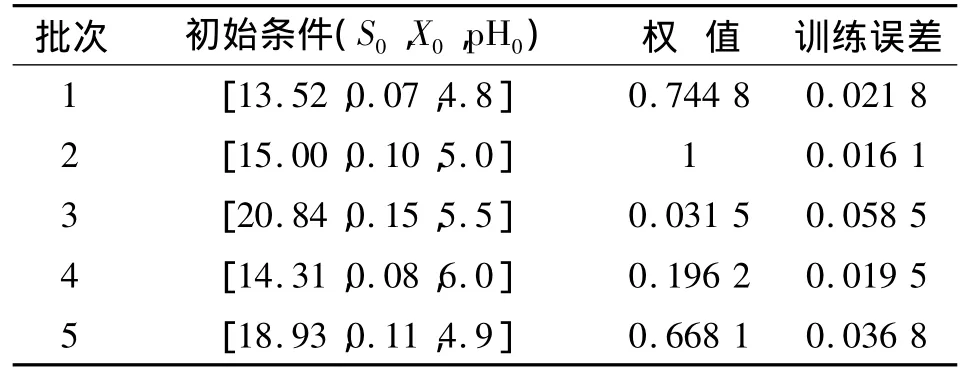
表3 BWRELM权值与训练误差Tab.3 Weights and training errors of BWRELM

综上所述，基于文中所提建模方法建立的青霉素发酵过程产物质量浓度软测量模型，与其他3种比较，预测精度更高，综合性能更好。

3 结语

针对发酵过程关键变量难以在线测量的问题，提出了一种基于批次加权正则极限学习机(BWRELM)的软测量建模方法，并以青霉素发酵过程为对象，实现了产物质量浓度的软测量。结合发酵过程中系统动态特性与初始条件密切相关的特点，以发酵批次初始条件之间的欧氏距离为相似度，通过相似度量化函数得到用于度量训练过程中各训练批次重要性的惩罚权值，区别对待各训练批次，提升模型预测精度，并且设计了一种惩罚力度更大的新的相似度量化函数，与常用量化函数相比，进一步改善了模型的性能。采用贝叶斯方法对RELM中的超参数进行自适应估计，降低了计算代价，而且不需要专门划分出验证集，可以有更多的样本数据用于训练。最后的仿真结果表明该算法的有效性，对解决同类问题具有一定的参考价值。

［1］Jimenez A，Beltran G，Aguilera M P，et al.A sensor-software based on artificial neural network for the optimization of olive oil elaboration process［J］.Sensors and Actuators，2008，129(2):985-990.

［2］HUANG G B，ZHU Q Y，Siew C K.Extreme learning machine:a new learning scheme of feedforward neural networks［C］//the International Joint Conference on Neural Networks.Budapest，Hungary:IEEE，2004:25-29.

［3］HUANG G B，ZHU Q Y，Siew C K.Extreme learningmachine:theory and applications［J］.Neurocomputing，2006，70:489-501.

［4］HUANGG B，DING X J，ZHOU H M.Optimization method based extreme learningmachine for classification［J］.Neurocomputing，2010，74:155-163.

［5］韩敏，李德才.基于替代函数及贝叶斯框架的1范数ELM算法［J］.自动化学报，2011，37(11):1344-1350.HAN Min，LIDe-cai.An norm 1 regularization term ELM algorithm based on surrogate function and Bayesian Framework［J］.Acta Automatic Sinica，2011，37(11):1344-1350.(in Chinese)

［6］胡义函，张小刚，陈华，等.一种基于鲁棒估计的极限学习机方法［J］.计算机应用研究，2012，29(8):2926-2930.HU Yi-han，ZHANG Xiao-gang，CHEN Hua，et al.Extreme leaming machine on robust estimation［J］.Application Research of Computers，2012，29(8):2926-2930.(in Chinese)

［7］XU J T，ZHOU H M，HUANG G B.Extreme learning machine based fast object recognition［C］//Information Fusion 15thInternational Conference on.Singapore:［s.n.］，2012:1490-1496.

［8］ZHANG R X，HUANG G B，Sundararajan N，et al.Multicategory classification using an extreme learningmachine formicroarray gene expresssion cancer diagnosis［J］.IEEE Trans Computational and Bioinformatics，2007，4(3):485-495.

［9］常玉清，李玉朝，王福利，等.基于极限学习机的生化过程软测量建模［J］.系统仿真学报，2007，19(23):5587-5590.CHANG Yu-qing，LI Yu-chao，WANG Fu-li，et al.Soft sensing modeling based on extreme learning machine for biochemical processes［J］.Journal of System Simulation，2007，19(23):5587-5590.(in Chinese)

［10］毛力，王运涛，刘兴阳，等.基于改进极限学习机的短期电力负荷预测方法［J］.电力系统保护与控制，2012，40(20):140-144.MAO Li，WANG Yun-tao，LIU Xing-yang，et al.Short-term power load forecasting method based on improved extreme learning machine［J］.Power System Protection and Control，2012，40(20):140-144.(in Chinese)

［11］DENGW Y，ZHANG Q H，CHEN L.Regularized extreme learningmachine［C］//Computational Intelligence and Data Mining，2009.CIDM’09.IEEE Symposium on.Xian:［s.n.］，2009:389-395.

［12］MacKay D JC.A Practical bayesian framework for back-propagation networks［J］.Neural Computation，1992，4(3):448-472.

［13］Huynh H T，Won Y.Weighted least squares scheme for reducing effects of outliers in regression based on extreme learning machine［J］.Int JDigital Content Technol Appl，2008，2(3):40-46.

［14］杨强大，王福利，常玉清.基于加权RBF神经网络的诺西肽发酵过程菌体浓度软测量［J］.化工学报，2008，59(10):2553-2560.YANG Qiang-da，WANG Fu-li，CHANG Yu-qing.Weighted RBF neural network based soft sensor of biomass in nosiheptide fermentation process［J］.Journal of Chemical Industry and Engineering(China)，2008，59(10):2553-2560.(in Chinese)

［15］HONG JJ，ZHANG J.Quality prediction for a fed-batch fermentation process usingmulti-block PLS［J］.Springer Proceedings in Physics，2010，135:155-162.