打造“悟”的三步曲

《说文》曰：“悟，觉也。”悟不是告诉，而是激励，是唤醒，是点化，是体验。在一次骨干教师培训交流课上，刘荣娇老师在“找次品”这节课上充分展示教师的主导作用，引领学生通过观察、对比、分析、反思、运用，在分三个层次运用天平“找次品”中体验“悟”的过程。

在充分感悟中寻找最优策略

师：三瓶口香糖中有一瓶次品，它更轻一些，你有办法把它找出来吗？

生：通过观察外包装，可以找出次品。

师：这是采用了观察法。如果外包装区别不大，怎么办？

生：称一下。

师：你会采用什么工具来称？

生：天平。

师：谁愿意来表演一下天平，称出这瓶次品？

[一名学生在同学的笑声中上台，打开双手模仿天平]

师：一边放两瓶，一边放一瓶，能找出这瓶次品吗？

生：不能。

师：那应该怎么做？

生1：天平两边各放一瓶。

生2：天平两边要放的瓶数必须一样多。

师：如果天平是平衡的，次品在哪里？

生：次品肯定就是天平外的那一瓶。

师：如果一边翘起，次品又在哪里？

生：翘起的那一边就是次品。

师：要称几次才能找到？有几种可能？

生：有两种可能，只需要称一次。

我们加大难度，现在有5个棋子，其中一个是次品，次品轻一些，请用天平找出来。

[生在小组合作中解决问题]

生1：我们是分成5（1、1、1、1、1），先称两个，如果不平衡，只需要称一次。如果平衡，再放另两个，需要称两次。

生2：我们是把5个分成5（2、2、1），天平一边放两个，如果平衡，剩下那个是次品，称一次。如果不平衡，把翘起的一边中的两个分开来再称一次，需要称两次。

师：我们发现，不管运气好坏，两次都能找出次品。

师：这批零件有2187个，其中有一个次品更轻一些，猜猜看，你认为要称多少次？

生1：100次。

生2：30次。

生3：1000次。

……

师：“天下难事必作于易，天下大事必作于细。”2187个太多了，我们可以采用化繁为简的数学思想，找到最好的策略来解决。

找次品最优策略的发现不可能一蹴而就，刘老师采取了“温水煮青蛙”的方式，从最简单的三瓶中找一瓶次品，再过渡到五个棋子，最后再引出下面片段二的九个零件。这样有梯度的设计有效地降低了学生寻找最优策略的难度，尊重了学生的学习方式和发展规律，为学生探究最优策略搭好了“脚手架”。而从2187个零件中找一个次品，她让学生大胆对所需次数进行猜想。数学方法理论的倡导者波亚利曾说：“在数学的领域中，猜想是合理的、值得尊重的、负责任的态度。”这样的猜想可以激发学生进一步探究的欲望，形成积极的思维态势，从而一步步进行数学知识的思考，感悟数学思想在解决实际问题中的初步运用。

在操作对比中领悟发现最优策略

师：9个零件中有1个次品，次品重一些，至少称几次就一定能找出？你能找出题目中的关键词吗？

生1：一定。

生2：至少。

师：你怎么体会这两个词？

生：用天平称的时候，要保证能找到次品的最少的次数。

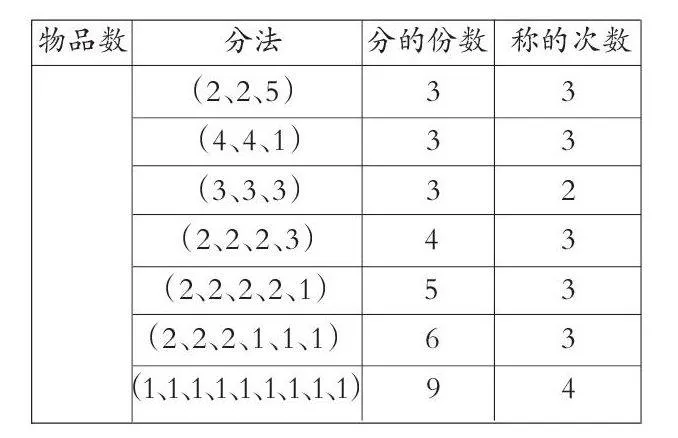
师：再用天平称的时候，有时会因为运气好而提前找到，但这并不能保证我们每一次都能有这么好的运气，所以在寻找规律时，我们要做最坏的打算。请小组合作，拿出学习单，完成表格。

师：现在你能看出哪种分法能最快找出次品吗？

生：第三种分法。

师：它是怎么分的呢？

生：这种分法是把9个平均分成了三份。

师：是不是平均分成三份的方法最好？你能不能举例验证？

在教学中采用小组合作学习的方式，形成了师生、生生之间的全方位、多层次、多角度的交流模式，通过小组合作探究找到了用天平在9个物品中找一个次品的各种方法，再通过比较发现了找次品的最优策略，进而有一种“豁然开朗”的感觉，达到领悟的效果。

四至六年级学段的学习目标指出：在解决问题的过程中，能进行有条理的思考，能对结论的合理性作出有说服力的说明，能表达解决问题的过程，并尝试解释所得的结果。学生通过合作探索、归纳总结出了“找次品”的最优策略，刘老师并不满足，而是让学生举例说明，以解释这个最优策略，利用不完全归纳法诱发学生自觉地分类、比较及运用，使得学生真正把握了找次品的方法，从而对得出的结论从感性认识上升为理性认识。在发现最优策略的过程中完成了“悟”的第二步。

在反思运用中证实最优策略

师：最优策略是把物品总数平均分成3份。可是为什么平均分成3份，所称的次数最少呢？请认真观察表格，每一种分法在第一次称后，一次可以排除几个正品？第一种分法，在天平两边各放两个，如果平衡，次品在哪里？

生：在剩下的5个之中。

师：那在天平上的4个就是正品，占总数的几分之几？

生：九分之四。

师：第二种分法可以排除几个正品？占总数的几分之几？

生1：九分之五。

师：第三种分法呢？

生2：九分之六。

师：第四种？第五种？第六种？

生3：九分之四。

师：最后一种？

生4：九分之二。

师：你发现了什么？

生：第三种能排除的正品占总数的比率最高。

师：一次可以排除的个数越多，那么称的次数就越少。

师：我们再来解决从2187个零件中找一个次品的问题，至少几次一定能找出次品？

……

通常的数学课堂里，在找到最优策略后，接着就是反复的练习以促进学生加深对方法的记忆和运用。可是刘老师并没有急于让学生去练习，而是采取了回顾反思的形式。“为什么平均分成3份，所需要的次数会最少？”这样的一个问题让学生陷入了沉思，也让我们陷入了沉思——数学广角中学习的内容是不是学生知道方法并会运用方法就够了？需要不需要让学生弄懂为什么这样做是最佳的？如何让知识点升华？刘老师采取的方式是让学生去证明自己找到的最优策略的合理性，引导学生用“一次称量后，排除的正品个数占总个数的几分之几”来验证最优策略，这种“证明感悟”的环节不仅加深了学生对最优策略的理解，而且丰富了学生的情感体验，使生涩的数学知识变得容易理解，更培养了学生严谨的学习态度。学生在经历迷惑和挫折以后，在刘老师的引导点拨下真正明白了最优策略的本质，经过思考后才产生觉悟。当然，个人认为“排除正品”的说法有一些别扭，是否可以改为“确定正品”，或是在第一次称后将次品的范围缩小到几个，学生理解起来会更容易一些。

教育家马寅初说：“对于书本知识，要深入钻研，过细咀嚼，独立思考，切忌囫囵吞枣，人云亦云，随波逐流，粗枝大叶，浅尝辄止。”刘老师在本课的教学中不仅重视结果，更重视了学习的过程，引导学生通过小组合作的探究活动，循着“由浅入深、逐步推进、合作探索、深化理解、自主运用”的思路，让学生在“猜想、对比、总结、验证、运用”的过程中真正体会到“化繁为简”的数学思想。自主的学习活跃了学生思维，激发了学生的灵感，学生在“感悟、领悟、觉悟”的三步中自由舒展，悟性灵动。（作者单位：江西省上饶市实验小学）

□责任编辑 汤金娥

E-mail：jxjyjxsxl@126.com