理论生长方程研究概述

段爱国 张建国

（中国林业科学研究院林业研究所 北京 100091）

理论生长方程研究概述

段爱国 张建国

（中国林业科学研究院林业研究所 北京 100091）

理论生长方程能对林木的生长及分布作出科学合理的描述。通过对几种主要理论生长方程的起源、应用发展现状及方程间错综复杂的关系予以了较为全面的阐述，旨在使人们对理论生长方程有个清醒的认识并科学、合理地使用之，进而拓宽其应用研究领导以及推动理论生长方程的深入发展。

生长方程; 起源; 进展; 关系

理论生长方程是指在生物生长模型研究中，根据生物学原理作出某种假设建立有关生物体大小的微分方程，解出并代入其初始条件或边界条件而导出的模型。它的特点包括逻辑性强、适用性较大、参数可作出生物学解释以及可从理论上对尚未观察的事实进行预测。

当人们考察树木的整个生长过程时，会发现它们的生长遵循一条“S”型曲线，尽管受到环境的影响会出现一些波动，但总的生长趋势是比较稳定的[1]。由于在一个具体的林分内，林分内单株树木的生长在理论上呈“S”型曲线，由单株生长所构成的林分整体生长亦呈“慢—快—慢”的态势，而且由分化所引起的林木径阶株数百分比累积分布也呈现“S”型状态。因此，“S”型或近似“S”型的理论生长方程可以应用于单株、林分及径阶水平的林木生长或分布，即可被用作构建一类、二类及三类模型。不同的理论生长方程适合描述的对象不同，就同一对象而言，“S”型方程的参数个数、结构组成及拐点取值情形对方程模拟精度具有至关重要的影响作用[1,2]。纵观理论生长方程的发展历程，其经久不衰、应用日渐广泛的内在原因可归结为两点：一是其理论根基的深厚；另一就是其数学表达式的灵活性及较强的可移植性。目前，对理论生长方程的研究已远远超出了方程原有的涵义。鉴于理论生长方程应用领域的广阔，本文对几种主要理论生长方程的起源、应用发展现状及方程间错综复杂的关系予以了较为全面的阐述，旨在使人们对理论生长方程有个清醒的认识并适时、合理地在林业统计上使用之，进而拓宽其应用研究领域以及推动理论生长方程的深入发展。

对于理论生长方程，目前研究、应用较多的主要有：坎派兹式[3]（Gompertz方程）、逻辑斯蒂式[4]（Logistic方程）、米切尔里希式[5]（Mitscherlich方程）、贝塔兰菲式[6]（Bertalanffy方程）、理查德式[7]（Richards方程）、舒马赫式[8]（Schumacher方程）和Korf[9]方程等七种。下面重点就这些方程的研究应用情况进行概述。

1 理论生长方程的发展现状

1．1 Gompertz方程

上述7种理论生长方程中，Gompertz和Logistic方程被提出的时间最早，且最初均用于描述种群增长及分布问题。

坎派兹式是由Benjamin Gompertz于1825年首先提出，用来描述人口衰亡及年龄分布状况。一个世纪以后，该式被用作生长曲线方程[10]，广泛地应用于生物学和经济学领域。Wright认为“以相对生长率作为测定指标的平均能力多少按一定的百分率下降”，即生长率与生长衰减因子的对数成比例，依此假设原理就可导出Gompertz式。1932年Winsor为使Gompertz方程更便于应用，将该方程写成如下（1）式。日本学者末田达彦[11]在研究树干半径生长曲线适合性及研究理论干曲线方程时应用了此式，段爱国等[12]（2003）应用该方程模拟林分直径分布时，其精度排在第4位。

其中，k ＞ 0, b ＞ 0。

也有一些学者在利用坎派兹式时采用另一种表达方式：

上野洋二郎（1988）应用（2）式对单木的生长进行了研究；吴承祯[13]（1998）将其应用到人工林直径分布结构的研究上，结果表明适合性良好。实质上，（1）式与（2）式并无多大区别，仅a值的取值范围略有不同而已。Gompertz方程存在一个拐点，仅由渐进线参数决定，致使方程的灵活性受到一定程度的影响而降低。

1．2 Logistic方程

逻辑斯蒂式是由比利时数学家Verhulst（1838）所首创，用于描述人口的增长规律，方程的微、积分形式分别为（3）、（4）式。之后Pear和Reed（1920）将其用来描述美国人口增长过程。逻辑斯蒂式大概是生态学上最著名的方程，自创立至今已有170多年，引起全世界学者广泛深入的研究，惠刚盈[14]（1995）在国内首次将该方程应用于林分结构的研究。该方程反映生物种群增殖率与环境中的营养物质之间存一种线性关系，这种线性关系是生物学上极为复杂关系的一种近似表达。方程的表达式可写为（5）式。应用该方程模拟林分直径分布时，其精度仅次于Richards方程[12]。

（5）式中C与（4）式中maxY均为上渐近线值，两者相等；为内禀生长率；x0、y0分别是x、y的初值，且C，q＞0 。逻辑斯蒂式在生态学和经济学中广泛地成功运用，主要是因为其具有营养动力学上的说理模型的性质，而且它是一条标准的S型曲线，而自然界和社会中大量的事物变化又均体现出这一规律[15]（李文灿，1990）。然而Logistic方程所建立的理论基础虽然颇合自然界的实际（自然界营养太缺乏，营养物质的增加立即引起增殖率的增加，几乎成正比），但在营养物质较丰富时（如在微生物的培养和发酵中），是不能成立的。鉴于此，崔启武和Lawson[16]（1982）提出了一个新的理论生长模型，该模型为马尔萨斯指数方程和逻辑斯蒂方程的融合与扩充。鉴于Logistic方程的拐点在渐进值的1/2处，张大勇[17]（1985）在原方程的基础上提出了如下（6）式。

方程中参数θ是一个常数，C，q＞0,（6）式的拐点可以在1/2左右取得，从而在理论上大大提高了逻辑斯蒂方程的灵活性。

孙洪刚等（2007）[18]就Logistic及其改进模型在杉木人工林胸高断面积模拟中的应用进行了深入探讨，发现对于某一具体植物种群,不同形式的Log istic模型的模拟精度主要受模型本身的影响，并在比较5种Logistic 模型模拟性能基础上，推荐张大勇（1985）[17]在探讨森林自疏规律时提出的Log istic改进模型，认为该改进模型参数最稳定, 模拟精度最高,为模拟杉木或其它相似生长进程人工林胸高断面积的首选模型。

1．3 Mitscherlich方程

米切尔里希式由Mitscherlich于1919年提出，用来描述植物对环境因子的反应，在农业和经济学中，此方程被称为“收益递减律”（Law of diminishing returns）原理。最初Mitscherlich所提出的方程形式为：式中，y ——收获量，x1,x2——控制增长的因子。

若把时间看成是一个最重要的影响树木生长因子，且仅取它为唯一的控制因子，则上式可化为最简。理查德（1969）把它称之为单分子式，其表达式形式可写为：

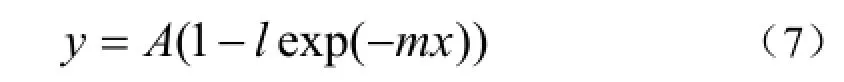
方程参数的涵义为：A —上渐近线值；l— 与y初值有关的参数；m — 内禀生长率。且A ＞ 0, m ＞ 0, 0 ＜l≤ 1。在以后的许多研究中，人们均习惯采用上式中当l=1时的二参数方程形式[19]，并取得了较好的效果。

1．4 Bertalanffy方程

贝塔兰菲式是由Von Bertalanffy（1957）基于德国著名生理学家Putter（1920）提出的表面积定律的基础上建立的。通过分析动物的生长，Von Bertalanffy发现在动物生长期间，动物的体重增长速率为同化速率与消耗速率之差，而后两者分别和同化器官的大小以及动物体重成比例。Cooper（1961）在研究美国亚利桑那北部西黄松林林分密度及断面积生长方程后认为，应用Bertalanffy方程进行林木分析可能比Logistic方程更佳，并建议将其引入森林生长研究中。该方程可表示为：

式中：F——同化器官重，W——体重，aR——同化速率，xR——消耗速率。

由相对生长关系，有F=rWm, 因此上式可变形为：

式中：η=ar。当x=0时，W=W0，则（8）式的积分形式为：

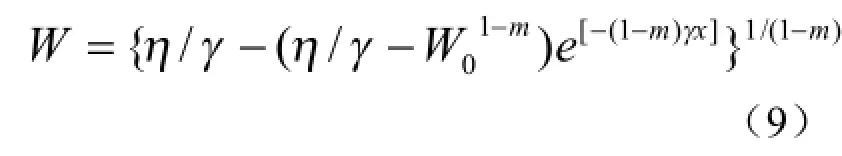
Richards认为上式中的m取值为2/3，这样Bertalanffy方程可简写为如下形式：

其中，参数A为y的最终值既上渐近值；参数B决定x=0时生长因子的大小，而参数k则与生长速度有关。Bertalanffy方程的优点在于它理论基础的严密性，揭示出了生长基础的生理机制。但这一理论形成时的研究对象为动物生长，具有一定的局限性，也正因为此，一定程度上限制了该方程在其它应用研究（如植物）中所能表现出的灵活性。

趣味个性互动抽奖是将微门户大厅与抽奖平台相结合，在活动抽奖前，活动主持人可以让读者发送一段自己在图书馆读书或参与活动相关的文字、照片、语音等，平台自动将读者的微信号导入抽奖池，参与抽奖。方式趣味，读者掌握极大的主动权，提高活动气氛。此方式在图创年会上，已经得到了很好的应用，带动了年会“高”、“嗨”、“翻”的活动气氛，每一轮抽奖，迎来了年会的气氛高潮！

1．5 Richards方程

在林学方面，描述树木生长及林分生长过程时，应用最广泛的就属Richards方程[21]，它是由理查德基于Von Bertalanffy生长理论扩展而来。Richards（1959）在研究植物的生长时认为，对植物生长而言，Bertalanffy方程（8）中的m的可能取值范围为m＞0。其实，该方程早被Mitscherlich于1919年报道过。世界各国在研究林木生长模型时多采用Richards方程，主要应用在以下几个方面：1）与林分密度有关的林分断面积生长模型[22～24]；2）树高生长及地位指数方面研究[25,26]；3）林分直径结构研究方面[12,27]。

Richards方程来源于Bertalanffy方程，（8）式中m＞0时有：

（当m＞1时，η、 γ＜0; 当0≤m＜1时，η、γ＞0）

上式的积分式（11）经简化整理可得Richards生长函数：

理查德方程的标志是它的灵活性，这个方程的价值在于它的精度和在树木与林分生长研究中比其它方程更多的应用。随着方程中m取值的变化，它可转化为其它形式的方程。

（1）m＜1时，（11）式可写为：

（12）式即为人们通常应用的Richards方程的表现形式[24,27]。

（2）m＞1时，（11）式可写为：

（13）式与Logistic方程的扩展式（6）式形式一致，仅参数不同。

（3）m=0时，（11）式变为Mitscherlich生长函数：

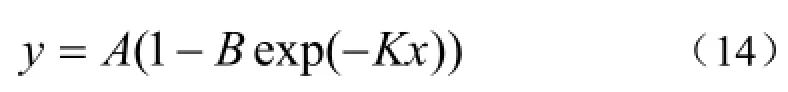
（4）m=2时，（11）式化为Logistic方程，这一点从考察两式的微分式可以明确地得到，也揭示了两方程间的微妙关系。

（5）m→1时，方程就转化为Gompertz生长函数，对此上野洋二郎等（1988）经过数学推导提出异议，指出该种情况下Richards方程为一指数方程。

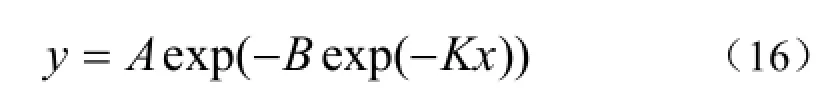
以上各式中，A，B，K＞0。

如上所述，Richards方程因为其深厚的理论基础及其形式的灵活多样而具有广泛的适应性、合理解析性和良好的预测性。后来，Schnute[28]（1981）基于简明的生物学原理——加速生长，导出了一个包含迄今为止所有理论生长函数的方程，被认为值得推广应用。其中有研究Bredenksmp[29]（1988）与杨荣启等[30]（1989）认为该方程能够描述Richards方程所不能描述的一些生物生长现象。但也有研究[31]认为Schnute方程无论是其假设、解的形式，还是反映生长曲线的特征值均与Richards函数相同，是Richards方程的另一种解的表达式。然而，从事实和研究结果来看，Richards方程还是存在不足之处[32]。张少昂[33]就曾对Richards方程的适用条件和其局限性进行了一些探讨，并提出了一种认为可以更适合描述树木或林分生长过程的新的理论生长方程。段爱国等（2006）[34]基于Richarchs函数，提出一种新的断面积分布模型——R分布，导出了其概率密度函数及累积分布函数，发现R分布对林分断面积分布能实现高精度的模拟,且其参数具有深刻的理论涵义。

1．6 Schumacher方程

舒马赫式是由Schumacher（1939）基于同龄纯林树木的生长百分比同年龄成反相关的假设原理而得出的一个较为简明的树木生长方程。方程的原始表达式为：

式中，V、A分别为林分材积和年龄，k为与林分立地指数和立木密度相关的常数值。对（17）式积分则有：

式中，b为0.4343k，a为林分材积最大值的常用对数。李久先[35]（1996）在应用Schumacher方程时采用如下形式：

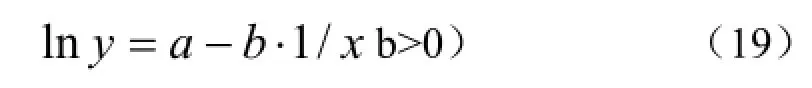
（19）式进一步可表示为：

（18）式中，如A的指数为c，则有：，对于这个Schumacher方程的拓展式，有些研究者[36]径直称为Schumacher方程，韩国学者[37]称其为Modify-Schumacher方程。Sahoo[38]（1998）曾用该式研究过立地指数曲线，得到较好的效果。同样，依上述转化步骤前式可表述为：

Schumacher方程存在两种表达形式即线性形式（19）和非线性形式（20），有研究认为[35]，其非线性形式较线性形式具有更好的拟合精度。

1．7 Korf方程

Korf方程由捷克斯洛伐克的林业工作者Korf于1939年首次提出。之后，又被重新发现几次，尤其是被瑞典林学家Lundqist（1957）利用该方程成功地构造了欧洲赤松及挪威云杉人工林的树高生长模型，故也有人称其为Lundqist-Korf方程。后来李凤日[39]和Zeide[1]相继运用Korf方程描述树高及胸径生长，取得较好效果。Korf方程的表达形式为：

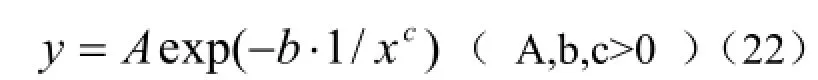
我们可以发现Korf方程（22）式与Schumacher方程的拓展式（21）具有完全相同的数学表达式，Korf方程中参数c值取1时即为Schumacher方程。Zeide[1，21]在研究树木直径生长时发现，相对生长率是年龄的幂函数，而不是指数函数，Zeide[1]将这种关系描述为一种相当简单的形式：

指数（-n,n＞0）为负值表明相对生长率随自变量而递减。将（23）式积分则有：（l，m，n为常数；m, n＞0 ），令A=el,b=)1/(+nm，c=n-1.则该积分式就转化为Korf（22）式。Korf方程存在一个拐点，位置为，当c＞0即（23）式中n＞1时,（c+1）/c ＞1,则的取值范围为（0，A/e）。李凤日[38]根据树木生长的一般特性，引用一般自治模型（张炳根，1990）)/(ydxdy=g（y），并根据Korf方程的微分形式假设，得出方程：

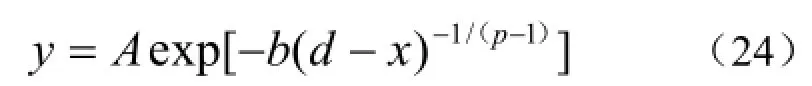
并称其为广义Korf生长方程，其中A，b＞0；d＞=0。进而根据p的不同取值情况导出二类方程：当p＞1,q＞0时上式拐点Ae-p范围为（0，A/e），此时方程称Korf—A型方程，指出树木生长均在此区域；当0＜p＜1时，拐点范围为（A/e,A），方程称Korf—B型方程；当p=1时，拐点为A/e，方程为Gompertz生长方程。

这样看来，Korf方程（22）式似乎较其广义形式（24）应用范围要小，对于这个问题可分析一下描述树木相对生长率与生长年龄（自变量）幂函数关系的（23）式。如前所述，当n＞1时，所积分出的Korf方程拐点范围为（0，A/e）；另外不妨讨论一下（23）式中n＜0的情形，这时Korf方程（22）式中c=n-1＜-1,c＜-1 ,从而0＜（1+c）/c=1/c+1＜1. 这样Korf方程（22）拐点范围为（A/e,A）；另外，当n=2时，c=1,方程拐点为Ae-2，方程表现为Schumacher生长函数；当n→∞时，拐点为A/e,方程表现为Gompertz方程。于是（23）式随n取值不同亦可表现为多种形式。最为重要的是，（23）式能揭示一个问题，那就是由于在自然界中，食物的缺乏和营养的不足是限制各类生物生长（包括树木）的主要因素，这样树木相对生长率大小随生长年龄的增大应为递减趋势，用幂函数表示的树木相对生长率随生长年龄变化的函数幂指数就一定应该为负值，那么，（23）式中n的取值就不能为负，树木生长曲线的拐点也就一般不出现在（A/e,A）范围。这一点从（24）式中就不能明显地体现出来。

2 理论生长方程的分类

以上概述了一些常用的理论生长方程，当然还有其它描述生长的理论方程如Hossfeld方程（Peschel,1938）以及Sloboda方程（1971）等。包括一向被看作概率密度函数的Weibull方程，也往往作生长方程使用，并且与部分理论生长方程相比，该函数表现出了较高的精确度和适合度[41，42]（Dolph,1991；Kimberley,1998）。

对于理论生长方程的分类，根据分类的依据及着眼点的不同存在不同的分类方式。Sweda和Koide[43]（1981）认为可分为四类，分别是经验方程、准理论方程、特殊理论方程和一般理论方程，并指出一般理论方程最适于描述树干半径的生长；Kiviste[44]（1988）从考察理论生长方程的的积分形式出发，将生长方程分为七类，将生长方程按拟合精确度排了个序；Zeide[21]（1993）在分析生长方程的基本结构后将生长方程分为LT—下降或LTD结构和T—下降即TD结构两类情形，另外将Sloboda等生长方程看作两种结构的混合形式，并根据挪威云杉测量数据得出。LTD结构生长方程具有更好的拟合性能。实际上，从以上对七种理论生长方程数学函数特性的分析可以看出，包括Weibull分布函数在内，树木的相对生长率表现为生长年龄的幂函数形式的生长方程有Schumacher方程和Korf方程；树木的相对生长率表现为生长年龄的指数形式的有Gompertz方程、Mitscherlich方程、Logistic方程、Bertalanffy方程和Richards方程；树木的相对生长率表现为生长年龄指数形式与幂函数形式的混合形式的有Weibull分布函数，这样分类的结果与Zeide的分类结果完全相同，并且清晰，一目了然。

[1] Zeide, B. Accuracy of equations describing diameter growth. Can. J. For. Res. 1989（19）:1283～1286.

[2] Zhang, J.G. Duan, A.G. Application of theoretical growth equations on modeling stands diameter structure of Chinese fir plantations. Forest Science. 2003.

[3] Gompertz,B. On the nature of the function expressive of human mortality, and on a new mode of determining the value of life contingencies.Phil.Transac Roy.Soci.London, 1825（115）:513-585.

[4] Verhulst,P.F. Correspondence Mathe-matique et Physiques, 1838（10）:113-121.[In French]

[5] Mitscherlich,E.A. Landwirt schaftli -che jahrbucher（Berlin）. 1919（53）:167-182.[In German.]

[6] Bertalanffy.L.Von. Quantitative laws in metabolism and growth.Quart. Rev.Biol. 1957（32）:217-231.

[7] Richards, F.J. Aflexible growth function for empirical use. J.Exp. Bot. 1959（29）:290-300.

[8] Schumacher, F.X. A new growth curve and its application to timber-yield studies.J.For. 1939（37）:819-820.

[9] Kiviste, A.K. Mathematical functions of forest growth. Estonian Agricultural Academy,Tartu,USSR. 1988.

[10] Wright,S.:Book review in J.Am.Status.Assoc. 1926（21）:493-497.

[11] Tatsuo Sweda, Takeo Umemura and Junici Tanaka. Applicability of growth equations to the growth of trees in stem radius（Ⅲ） accuracy of projections. J Plann. 1985，327-331.

[12] Duan, A.G., Zhang, J.G. Tong, S.Z. Application ofsix growth equations on stands diameter structure of Chinese fir Plantation. Forest Research. 2003（16）423-429.

[13] 吴承祯，洪伟.杉木人工林直径结构模型的研究.福建林学院学报，1998（2）：110-113.

[14] 惠刚盈，盛炜彤.林分直径结构模型的研究.林业科学研究，1995（2）：127～131.

[15] 李文灿.对Logistic方程的再认识.北京林业大学学报，1990（2）：121～127.

[16] 崔启武，Lawson.一个新的种群增长数学模型——对经典的Logistic方程和指数方程的扩充.生态学报，1982.

[17] 张大勇，赵松龄.森林自疏过程中密度变化规律的研究.林业科学，1985（4）：369～374.

[18] 孙洪刚，张建国，段爱国，等. 5种Logistic模型在模拟杉木人工林胸高断面积分布中的应用. 林业科学研究，2007,20（5）：622-629.

[19] Tatsuo Sweda. A theoretical stem taper curve（Ⅱ）. J Plann. 1988，199～205.

[20] Sweda, T. Theoretical growth equations and their application in forestry. Bull.Nagoya Univ.For. 1984（7）:149-260.

[21] Zeide, B. Analysis of growth equations. For. Sci. 1993（3）: 594～616.

[22] Pienaar, L.V., and K.J. Turnbull. The Chapman-Richards generalization of Von Bertalanffy’s growth model for basal area growth and yield in even-aged stands. For. Sci. 1973（1）:2～22.

[23] 张少昂.兴安落叶松天然林林分生长模型和可变密度收获表的研究. 东北林业大学学报，1986（3）：17～26.

[24] 唐守正.广西大青山马尾松全林分整体生长模型及其应用.林业科学研究，1991（增刊）：8～21.

[25] Ana Amaro, David Reed. Modeling dominant height growth: eucalyptus plantations in Portugal.Forest Science, 1998（1）:37～46.

[26] Mark O. Kimberley, Nick J. Ledgard. Site index curves for pinus nigra grown in the south island high country,New Zealand.New Zealand Journal of Forestry Science. 1998（3）:389～399.

[27] Ishikawa, Yoshio. Analysis of the diameter distribution using the RICHARDS distribution function （Ⅲ） [J]. Relationship between mean diameter or dameter variance and parameter m or k of uniform and even -aged stands.J Plann. 1998（31）: 15～18.

[28] Schnute J. A versatile growth model with statistically stable parameters. Can. J. Fish. Aquat. Sci. 1981, 1128～1140.

[29] Bredenksmp B V, Gregoire T C. A forestry application of Schute’s generalized growth function.For. Sci., 1988（1）: 26

[30] 杨荣启等.史纳德生长函数式在台湾人工林林分结构分析上的应用.中华林学季刊，1989（3）:3～17.

[31] 李凤日等. Richards函数与Schnute生长模型的比较.东北林业大学学报，1993（4）：15～24.

[32] 王冬梅. Richards生长函数在天然落叶松林分中应用的研究.北京林业大学硕士学位论文，1987,111p.

[33] 张少昂，王冬梅. Richards方程的分析和一种新的树木理论生长方程.北京林业大学学报，1992（3）：99～105.

[34] 段爱国，张建国，童书振.2006.应用R-分布模拟杉木人工林林分断面积累积分布的研究.北京林业大学学报，28（3）：86～94.

[35] 李久先. 三种生长模式在红桧人工林生长适用性之探讨.中华林学季刊，1996（2）3～14.

[36] D.奥尔德著.森林材积估测和收获预估（卷2—收获预估）.联合国粮食及农业组织, 1980,47p.

[37] Sang Hyun Lee. Developing and comparing site index curves using polymorphic and anamorphic equations for Douglas-fir. Jour. Korean For. Soc. 1999（2）:142～148.

[38] T.K.Sahoo,P.S.Chauhan. Site index curves for pinus roxburghii sergeant plantations Indian Journal of Forestry, 1998（3）:214～216.

[39] 李凤日.兴安落叶松天然林直径分布及产量预测模型的研究.东北林业大学学报, 1987（4）：8～16.

[40] 李凤日.落叶松人工林林分生长与收获模型.博士学位论文.北京林业大学, 1996.

[41] DOLPH,K.L. Polymorphic site index curves for red fir in California and southern Oregon.USDA For.Serv.Res.Pap. PSW-206, 1991,18P.

[42] Mark O.Kimberley. Site index curves for pinus nigra grown in the south island high country,New Zealand.New Zealand Journal of Forestry Science, 1998（3）:389-399.

[43] Sweda, T., Koide, T. Applicability of growth equations to the growth of trees in stem radirs（I）Application to white spruce. J.Jap.For.Soc., 1981,113～124.

[44] Kiviste, A. K. Mathematical functions of forest growth. Estonian Agricultural Academy, Tartu, USSR.（In Russion.） 1988.

Research progress of theoretical growth equations

DUAN Ai-guo, ZHANG Jian-guo
（Research Institute of Forestry, CAF; Key Laboratory of Tree Breeding and Cultivation, State Forestry Administration, Beijing 100091）

Theoretical equations can scientifically and reasonably describe the growth and distribu- tion of forestry. This paper relatively comprehensively elaborated the origin, present situation of application and development, complicated relationship among equations of theoretical equations, in order to make people have a clear knowledge about theoretical equations and scientifically use them, and make application fields get wide and promote the further development of theoretical equations.

Growth equations; origin; progress; relationship

S758.8

A

1004-7743（2013）01-0001-07

2012-09-13