垂线偏差对隧道贯通误差的影响规律及影响值计算

周 亮，沈云中，陈秋杰

一、引 言

由于GPS技术的相对定位精度较高，其应用于隧道平面控制测量优势明显。然而，GPS定位成果属法线系统；施工测量时，引测方向进洞及洞内导线测量均是以垂线为准的［1-2］。法线和垂线系统有差别，且地面点的垂线偏差很难准确测定。随着全球重力场模型精度的不断提高，利用全球重力场模型EGM2008［3］，即可解算地球表面上任意一点的模型垂线偏差［4］。该模型采用了GRACE卫星跟踪数据、卫星测高数据和地面重力数据等，空间分辨率约为 5＇（约为 9 km）。

贯通误差包括横向、纵向、竖向3个分量，满足横向贯通误差是关键。目前在计算隧道贯通误差时较少考虑垂线偏差的影响，势必对隧道后续测量方案的制订、施工等产生不利影响。为此本文分析了垂线偏差对隧道贯通误差的影响规律，绘出了全国垂线偏差等值线图，并结合高铁长大隧道计算垂线偏差对贯通误差的影响值。

二、垂线偏差对隧道贯通误差的影响

根据大地测量学，以法线为基准的观测方向和以垂线为基准的观测方向之间的差值为［5］

式中，ξj和ηj为测点j的南北垂线偏差分量和东西垂线偏差分量；A为方位角；α为高度角。

假设i、j、k组成的角度为βj，则以法线为基准的角度和以垂线为基准的角度的差值为

以上两种角度的关系为

根据式（1）和式（2）可知，当α≈0时，也就是两点的高程相当时，垂线偏差对观测方向的影响值ΔL≈0。对某个角度，当3点基本在同一高程面上时，Δβ≈0。洞内导线测量时，导线多为直伸型，式（2）的量值为零，即洞内导线测量受垂线和法线差异的影响极小。洞口控制点与投点间存在高差，控制点之间也存在高差，坐标方位角向洞内传递时必定会受垂线偏差的影响，从而增大横向贯通误差。

1.从两端洞口进洞对贯通误差的影响规律［1］

如图1所示，A和B为洞外GPS的控制点，1、2、3号点为洞内导线点。测量时以A—B为定向边，测量出A—1的方向，进而确定点1，逐步向洞内延伸。此过程中，垂线偏差对横向贯通误差的影响反映在两个角度上:βA和β1。由式（2）得

同理

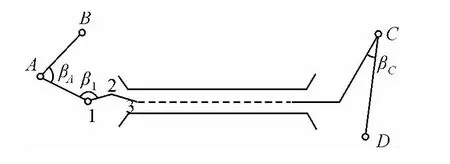
图1 洞口引测进洞关系图

假设在局部地区各点垂线偏差符号相同，大小也相等，那么同一条控制边的正反方向垂线偏差改正符号相同，大小相等，即ΔLA1=ΔL1A。从A—B定向边方位角推算至1—2边方位角时，垂线偏差对方向的总影响为

根据式（6），垂线偏差的影响最后归结到定向边坐标方位角的影响。垂线偏差对横向贯通误差的影响公式为

式中，S为A点至贯通面的垂直距离。当点A和点B高程基本相等时，即αAB≈0时，Δ横≈0。

据此得出结论:两端洞口GPS定向边的两个控制点基本等高时，垂线偏差对横向贯通误差的影响几乎为零。若定向边两端控制点的高程与洞口设计高程基本相等，那么将会更好地减小垂线偏差的影响。

2.从斜井洞口进洞对贯通误差的影响规律［1］

如图2所示，点A和点B为斜井口GPS控制点，点E为斜井底部与隧道的交接点。对于斜井直伸部分的任意导线角i-j-k，由于

由式（2）可推得

图2 斜井引测进洞关系图

当斜井为直伸且坡度均匀时，因为αji≈-αjk，则有Δβj≈0。在斜井入口处，若控制点A、B基本等高，即αBA≈0，则有 ΔLBA≈0。在斜井底部，因E和F点基本等高，即αEF≈0，则有ΔLEF≈0。则

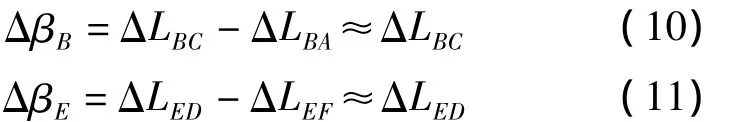
假设点B和点E处垂线偏差符号相同且大小相等，斜井为直伸型并坡度均匀，可得AED≈ABC+180°，αED≈-αBC，依据此处两式推导可得垂线偏差对方向传递的总影响公式为

据此可得出结论:当斜井为直伸型且坡度均匀，洞口GPS定向边两控制点高程基本相等时，垂线偏差对横向贯通误差的影响几乎为零。

3.考虑垂线偏差影响的贯通误差计算［1］

垂线偏差属于系统性偏差，不具有随机性，不能用简单均方的处理手段来处理垂线偏差对贯通误差的影响值和用常规方法计算得到的中误差。从安全角度考虑，按最不利情况进行估计。垂线偏差对贯通误差的影响值不能与常规方法计算的中误差综合，只能与极限误差综合。因此，考虑垂线偏差影响时，横向贯通误差极限误差的估计公式为

而

式中，m洞外为平面控制网误差对横向贯通误差的影响值中误差；m洞内为洞内导线测量误差对横向贯通误差的影响值中误差；S为洞口GPS坐标传算起点至贯通面的垂直距离；ΔL为定向边坐标方位角的垂线偏差改正值。

三、全国垂线偏差计算及分布

1.垂线偏差计算方法

大地测量学［6］通常将垂线偏差U分解为南北方向分量ξ和东西方向分量η。根据文献［7］，利用EGM2008模型实现了任意点的垂线偏差值计算。其计算公式为

2.全国垂线偏差等值线图

根据我国地理位置，按1°×1°进行垂线偏差计算，绘制全国1°×1°垂线偏差等值线图。依据计算结果，垂线偏差最大值为:ξ=-23.8″，η=-34.3″，U=41.7″，位置在云南东南部，其经纬度为东经102°、北纬 24°。

依据式（2）、式（14）计算我国境内垂线偏差较大处对横向贯通误差的影响值。垂线偏差影响进洞定向精度，下面计算的影响值仅是隧道一端进洞边定向误差对横向贯通误差的影响值。计算时的假设条件为:定向边方位角为45°，投点至洞口点方位角为225°，定向边高度角10°，投点至洞口高度角为45°，洞口至贯通面距离为2 km。情况见表1。在这些垂线偏差较大的区域，如不进行垂线偏差影响改正，将会给隧道贯通测量带来极大困难。

表1 国内部分垂线偏差较大位置及对贯通误差影响值

四、实例分析

结合国内高铁建设中的3个隧道项目，利用EGM2008模型计算垂线偏差，部分结果见表2。

表2 某隧道部分控制点垂线偏差值 （″）

在隧道进出口和斜井口，选择最合适的一对点进行定向，并向洞口进行投点，根据式（2）计算垂线偏差对定向的影响误差，见表3。

通过式（12）计算得出各贯通段垂线偏差对贯通误差的影响值，见表4。

从表4中可以看出，垂线偏差对贯通误差的影响值比较大，大部分超过5 mm，需要进行改正。利用表4结果，根据式（13）可计算出顾及垂线偏差影响的贯通误差值。

表3 垂线偏差对隧道洞口定向方位角影响值

五、结论与建议

1）根据对高铁项目中长大隧道数据的分析及验证，GPS技术应用于长大隧道平面控制测量时应考虑垂线偏差影响。此影响具有系统性，即隧道开挖长度越长，垂线偏差对横向贯通影响值越大。

2）垂线偏差对观测方向的影响，取决于测站垂线偏差的量值。隧道两端洞口定向方向的垂线偏差影响值大小决定了垂线偏差对横向贯通误差的影响值大小。

3）GPS洞外平面控制点应尽量埋设在等高面上，以便消除垂线偏差对横向贯通误差的影响。

4）建议向洞口投点时经纬仪或全站仪使用7″甚至更精确的水准泡，且在测量前作好检校，以提高精度。

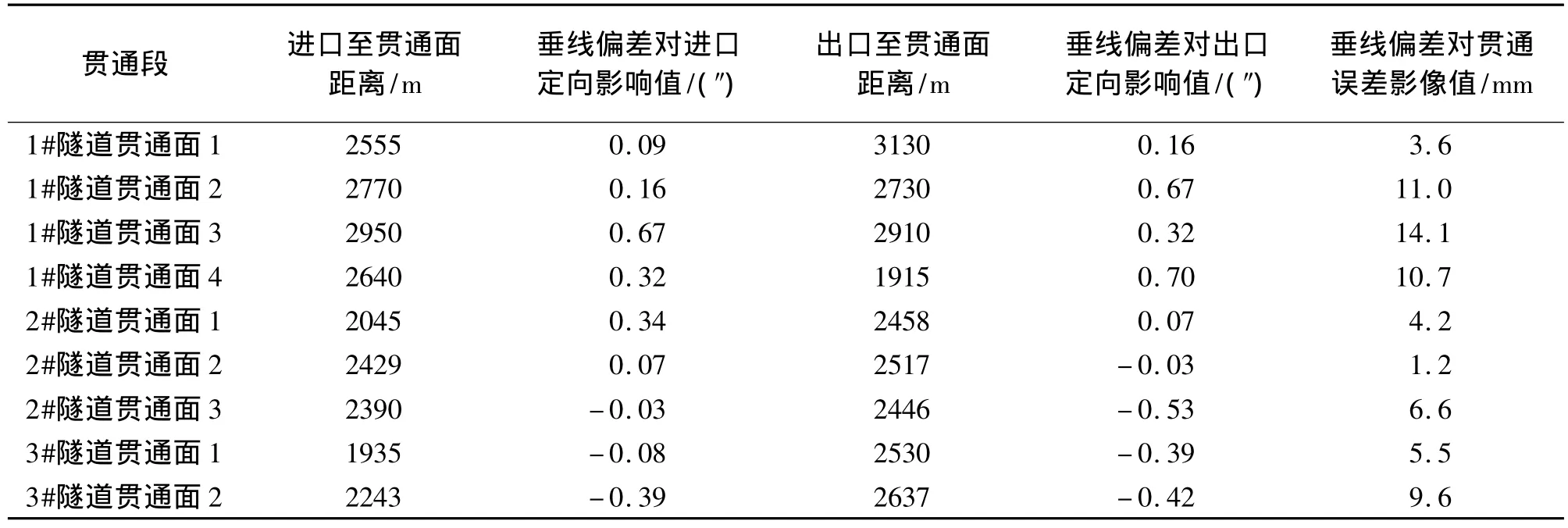
表4 垂线偏差对隧道贯通误差影响值

［1］ 王文通，张项铎.垂线偏差对隧道横向贯通测量影响的研究［J］.隧道建设，2006，26（6）:17-19，23.

［2］ 张项铎.隧道GPS网布测中有关问题的探讨［J］.中国铁道科学，2001，22（6）:73-79.

［3］ 魏德宏，张兴福，冯冬宁.基于EGM2008重力场模型的区域似大地水准面确定［J］.地矿测绘，2009，25（3）:17-18.

［4］ 肖荣健.地球重力场模型及其在隧道测量中的应用［D］.成都:西南交通大学，2007.

［5］ 路伯祥，范东明，熊永良，等.垂线偏差对隧道贯通误差的影响［J］.工程勘察，1998（3）:56-59.

［6］ 施一民.现代大地控制测量［M］.北京:测绘出版社，2003.

［7］ 张子占.卫星测高/重力数据同化理论、方法及应用［D］.北京:中国科学院，2008.