BP神经网络在温度二次仪表零位电压补偿的应用
石良喜
(广州计量检测技术研究院,广东广州 510030)
0 引言
温度二次仪表在各行业中使用相当广泛,随着使用环境的改变,其内部环境的温度也会改变,导致温度二次仪表内部传感器原件及集成电路板零位电压产生漂移,从而产生温度二次仪表的测量误差,因此有必要进行温度补偿,减少测量误差。本文选用数字传感器DS18B20对二次仪表所处的环境温度进行测量,运用人工神经网络与BP算法相结合,得出非线性温度补偿数据列表。利用MATLAB工具,对二次仪表的零位测量电压的温度漂移进行补偿,通过模拟仿真,对比分析补偿前后的测量结果,使用该方法,提高了温度二次仪表的测量精度,减少了系统的测量误差,对二次仪表的计量性能起着重要作用。
1 二次仪表的零位电压温度特性测量
针对二次仪表的使用环境,二次仪表内部环境温度的测量,测试温度为-40℃~80℃,在输入为零的条件下,利用单片机模块来采样二次仪表的零位电压值。零位电压温度特性的测量系统如图1,ADC及DAC分别采用A/D转换器和D/A转换器,可以采用独立的A/D及D/A芯片[1],本文中分别指单片机中的A/D和D/A模块。

图1 二次仪表零位电压温度特性测量系统框图
硬件电路的设计,具体如图2所示。这里主要选用数字温度传感器DS18B20与单片机89C51作为主元件,数字温度传感器DS18B20工作方式为外部电源供电方式,与单片机89C5的P1.7管脚相连;整个的硬件电路较简单,只需要外接入一个4.7kΩ的电阻,即可实现二次仪表零位电压温度特性的测量。

图2 零位电压温度特性测量电路连接图
通过测试,得出零位电压温度特性曲线如图3所示。

图3 零位电压温度特性曲线图
由图3可知,该二次仪表的零位电压温度特性呈非线性,特性曲线规律性不明显。通常采用的方法有硬件法和软件法,但硬件法存在调试困难[2],补偿的效果不明显的缺点,一般采用软件法尤其是人工智能法可以弥足这些不足[3]。
2 零位电压温度漂移补偿方案
针对二次仪表的零位电压温度特性呈非线性,为了有利于输入信号的数字处理,这里运用人工神经网络,采用BP算法,利用BP神经网络的非线性拟合和泛化能力,可以有效地对二次仪表的零位电压进行非线性补偿。具体方案如图4所示。
二次仪表在零输入的条件下,即所检测到的信号为零,X=0。利用DS182B20及信号调理电路,采用在不同温度条件下传感器的温度特性,得到二次仪表的传感器的温度特性为
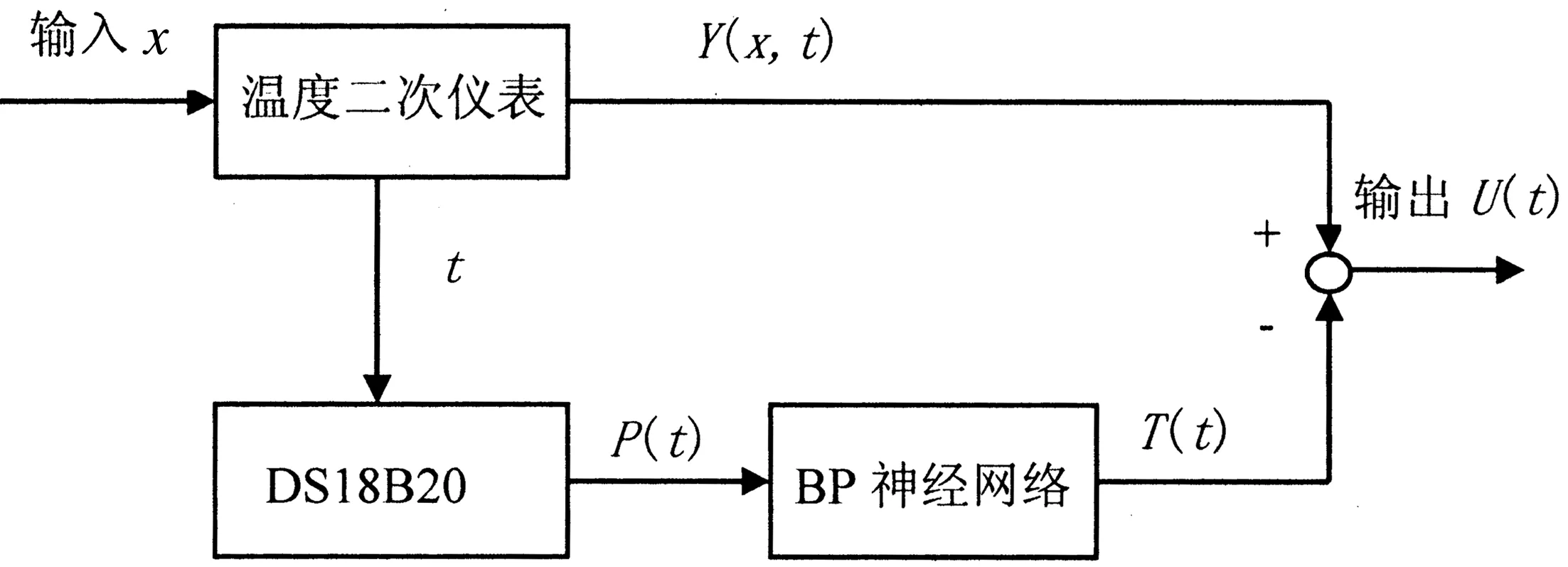
图4 零位电压温度漂移补偿框图
Y(x,t)=Y(0,t);t=t1,t2,t3……,tn
利用采样数据设计人工神经网络结构,编写程序,训练人工神经网络,对二次仪表的温度特性进行拟合,得到温度范围内任意温度下二次仪表零位电压的温度特性拟合数据[4]。训练后的人工神经网络特性为T=f(t),t为任意值。由于人工神经网络具有非线性拟合能力和泛化能力,把任意温度下传感器零位下电压的输出作为人工神经网络的训练目标值,经过训练以后,得到
T=f(t)=Y(0,t),t为任意值,即 T-Y=U(t)=0,从而传感器的零位电压得到补偿。
3 补偿模块设计及仿真
根据图4所示的补偿系统框图搭建二次仪表零位值的温漂补偿模块,如图5所示。图5中,input3为补偿前的传感器输出;display1为补偿后的二次仪表的输出值;display2为补偿值;dis⁃play3为人工神经网络模块的输出。其中input2为20℃时的电平值,由二次仪表感温部分产生的电压作为基准电压。

图5 零位电压温度补偿模块框图
本文中神经网络模块为单输入单输出系统,则输入层和输出层都只具有一个神经元节点。神经网络模块选用常见的双层结构[5],隐层节点数根据经验公式n=ni+n0+a=1+1+9=10;其中的n为隐层神经元节点数;ni为输入层神经元节点数;n0为输出层神经元节点数;a为[1,10]间的任意常数。
由于二次仪表的温度特性测试范围-40℃~80℃,则神经网络的输入矩阵PR=[-40,80]。根据常用的方法选择输入层到隐层传递函数为tansing,隐层到输出层的传统函数为purelin,学习函数使用learned,性能函数为mse,学习速率n可取1。利用newff()函数初始化神经网络模块的命令为 net=newff([-40,80],[10 1],…)。将传感器温度特性测量数据分别存入P、T两个矩阵作为训练数据[6],利用MATLAB中的神经网络训练函数train()对初始化好的神经网络模块进行训练。train函数将默认使用变梯度反传算法进行训练[7]。训练步数的选择可由语句net.trainParam.epochs=500定义,该语句定义了一个500步的训练步数。令训练后的网络名称为net,便可以使用下面的语句对网络进行训练:[net,tr]=train(net,P,T,[],[])。
4 结论
通过仿真可知,补偿后的零位电压值的温度特性得到较大的改善,如图6所示。
由图3与图6中的数据可计算出,在-40℃~80℃范围内,零位电压的温度误差由原来的26.83%降低到2.87%。如进行更深入的研究,学习速率能取到小于1的值,适当增加训练步数,可以进一步提高补偿精度。此外,该方法也可应用于其他计量器具的灵敏度温度特性的补偿,为其他计量器具中的电测部分提供一种较好的温漂补偿方法。
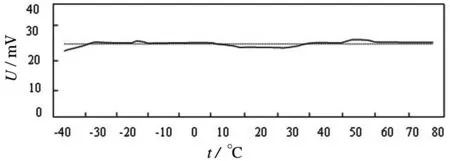
图6 引入BP与神经网络补偿后的零位电压温度特性曲线图
[1]张克.温度测控技术及应用[M].北京:中国质检出版社,2011.
[2]朱家良.温度显示仪表及其校准[M].北京:中国计量出版社,2008.
[3]李邓化.智能检测技术及仪表[M].北京:科学出版社,2012.
[4]张德丰.MATLAB神经网络编程[M].北京:化学工业出版社,2011.
[5]张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2012.
[6]董志成,任强.基于BP神经网络的减振器示功图识别方法[J].机电工程,2012(08):929-931.
[7]MATLAB中文论坛.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社,2010.

