计及多频率调节因素的孤岛频率协调控制方法研究

王 超，徐建源，李家珏，张 涛

(1．沈阳工业大学，辽宁 沈阳 110870;2．辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006)

国内外曾多次发生过电网故障导致系统孤岛运行引发大面积停电事故［1－2］。经验表明:系统处于孤岛运行状态时，影响其频率变化的因素复杂，系统维持大扰动下频率稳定的能力不断下降［3］。当受端系统的联络线因故障断开，则与大电网失去电气联系而形成孤岛。与大电网支撑下的系统频率动态变化特性相比，孤岛运行状态中的频率变化敏感性更高，频率变化更加难以控制［4－6］。因此，研究系统在成为孤岛后的频率及影响频率的动态因素对于低频减载方案的合理设计具有重要意义。

在电力系统孤岛运行方式下，由负荷控制转为频率控制是其最突出的特点［7］，要求发电机侧调频控制系统具备符合要求的静态和动态响应特性，以保证在用户负荷变化的情况下自动保持电网频率稳定［8－10］。为适应孤岛运行状态下系统频率变化的高敏感性，应考虑频率变化过程中发电机调节因素与负荷频率特性调节因素的综合约束，设计出能保证系统安全稳定运行的低频减载方案。

本文针对某实际电网，在PSASP上建立其仿真模型，研究该系统成为孤岛后的频率动态变化过程及影响因素。在该系统中考虑发电机调速器模型与负荷频率特性的综合影响，仿真研究了各方案对频率调节的性能，并针对系统所存在的问题提出建议。

1 建立频率稳定分析的动态数学模型

目前，逐步积分法是应用于电力系统稳定性评价的主要方法。它通过对微分方程的积分求解判断系统的稳定性。该方法的核心思想是采用“系统同一频率”的假设，将潮流方程和频率微分方程迭代进行求解。

在频率的动态过程分析中，“系统同一频率”假设就是忽略了系统中各发电机转子间的相对摇摆，认为系统没有同步稳定的问题。在此，将“系统同一频率”定义为其惯量中心的角速度ωsys，有:

系统频率动态过程方程为

式中:J为系统各发电机的转动惯量之和;i=1，2，…，n为发电机序号;第i台发电机的机械功率和电磁功率为Pmi、Pei;系统总加速功率为Pacc。

对于第i台发电机，其转子运动方程为

式中:Ji，Fi为第i台发电机的转动惯量和其所占系统总转动惯量的比例;Pai为第i台发电机的加速功率。

仿真计算中静态特性负荷模型可用二次多项式表示，即:

式中:UN为额定电压;PN和QN为U=UN时的有功和无功功率。

各个系数可根据实际的电压静态特性用最小二乘法拟合求得，满足:

由式 (1)和 (2)可见，有功和无功功率都含有3个分量:第一个与电压的平方成正比，是恒阻抗部分消耗的功率分量;第二个与电压成正比，是恒电流分量部分;第三个是恒定功率分量部分。

负荷的频率调节系数KL可由下式求出:

负荷的频率调节系数KL因负荷的性质不同，可能在相当大的范围内变化。典型取值是1%～3%。

2 孤岛运行频率稳定性分析

在孤网运行方式下，当机组侧或用户侧功率变化时，会引起系统频率较大变化，进而导致机组转速大幅波动，造成机组停机，同时也容易使电网瓦解。

2.1 孤网运行的频率特点

电力系统的频率是同步发电机产生的交流正弦电压的频率。在稳态运行条件下，发电机组同步运行，整个电力系统的频率相等。系统频率与发电机组的转速以及角速度存在如下关系:

汽轮机转子力矩平衡方程为

式中:p为发电机转子极对数;n为发电机组的转速;f为电力系统的频率。

由式 (11)可以看出，转子角速度的变化率与汽轮机的力矩差成正比。当汽轮机所受力矩发生变化时，发电机组的角速度将发生变化，引起发电机组转速的变化以及系统频率的变化。由此可知，负荷与发电机出力之间的不平衡量是影响系统频率变化的关键因素。加之孤网容量较小，负荷与发电机的扰动量相对值较大，其对孤网频率产生的影响更为明显。

2.2 发电机与负荷特性对孤岛频率的综合影响

在受端系统中，电力系统负荷的有功静态频率特性取决于负荷的组成。由于负荷种类不同，负荷与频率的关系也不同，表1为几种典型的负荷频率特性。

表1 几种典型负荷的频率特性

就总体而言，负荷的有功功率PL∝fn(n=0，1，2…)与整个系统的负荷功率和频率关系可以表示为

式中:PL为系统频率为f时负荷的有功功率;PLN为系统频率为额定值fN时负荷的有功功率;ai为各类负荷所占比例，

取PLN、fN为基值，将 (12)式表示为标幺值形式:

在实际系统中，允许的频率变化很小，此时负荷的功率与频率关系可近似为一条直线。将 (13)式对应的曲线在额定值附近线性化，如图1所示。

图1 负荷有功功率－频率静态特性

从有功负荷的功频静态特性曲线上可以看出，当系统有功负荷或有功电源的变化引起频率偏移时，负荷的频率调节效应起减小偏移、促进频率稳定的作用。这种调节作用的大小取决于KL的大小。在实际运行以及仿真计算中，也常常把不考虑机组备用容量时的系统有功缺额与其引起的系统问题频降的比值记为负荷的频率调节效应系数。

在送端系统中，发电机模型及其参数的确定是影响频率动态过程仿真分析的关键因素。本文通过采集电网大电源损失事故的实测频率数据，对发电机调速器模型及参数进行不断修正，采用时域仿真的计算方法来复现实际情况，通过分析得出结论如下。

a． 若发电机采用机械液压式调速器模型 (I型)时，功率脱落事件的仿真曲线与实际频率曲线存在较大差异，仿真曲线均呈振荡状态，与实际频率缓慢回升的情况不相符;将其参数调整后，虽然仿真曲线与实测曲线比较吻合，但调整后的参数已超出了合理范围，失去了实际的物理意义。

b． 若发电机采用电液调速器模型，可以保证在参数不超出合理范围的情况下较准确地拟合实测频率动态过程。从拟合结果看，仿真曲线与实际频率动态过程的主要指标基本吻合:达到频率最低点的时间基本一致，仿真最低点略低于实际最低点。

3 实际电网中弧岛频率的协调控制方案

以某地区实际网架结构为例，该地区电网通过新建500 kV变电站与系统主网相连，而与相邻区域电网的联络线解列运行，若发生500 kV联络线故障，将导致该区域电网孤岛运行。图2为该地区电网接线示意图。

图2 某地区电网接线示意图

3.1 实际电网中的孤岛频率特性

若发电机采用Ⅰ型调速器模型，功率脱落事件的仿真曲线与实际频率曲线存在较大差异，仿真曲线均呈振荡状态，与实际频率缓慢回升的情况不相符;将其参数调整后，虽然仿真曲线与实测曲线比较吻合，但调整后的参数已超出了合理范围，失去了实际物理意义。

当该地区的2台热电机组采用电液调速器模型(Ⅳ型)时，采用不同低频减载方案时的频率特性曲线如图3所示。

在其他条件均不变的情况下，当切除负荷频率特性系数为K=1.6和K=2.6情况下的频率曲线如图4所示。

图3 Ⅳ型调速器模型下系统频率特性曲线

图4 Ⅳ型调速器模型下系统频率特性曲线

由仿真结果可知，在发电机采用电液调速器模型时，低频减载方案中切除负荷频率特性系数K小的负荷比切除K大的负荷更有利于快速恢复系统频率;若切除负荷频率系数过大的负荷，则有可能发生频率崩溃。

3.2 孤岛频率协调控制方案的优化

设系统开始正常运行，且系统所有机组在额定功率下运行，系统运行机组的总额定容量为1 500 MW，负荷有功功率为1 300 MW，系统惯性常数约为10 s，系统内的其他负荷忽略不计。表2为兴安地区原低频减载整定表。

表2 某地区原低频减载整定表

现对每轮次低频减载装置所接的负荷按如下优化协调控制方案分配。

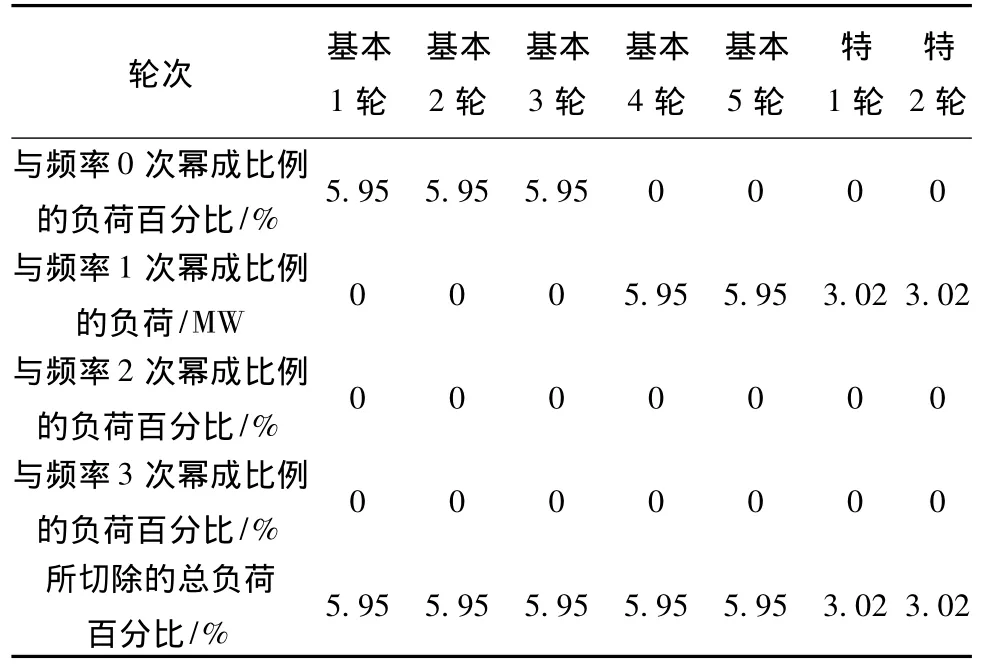
表3 优化的孤岛频率协调控制方案整定表

图5为2种频率协调控制方案下系统频率的动态恢复过程曲线。

由仿真结果可知，优化后的频率协调控制方案可使系统频率有效地恢复至工频左右，且频率最低点高于原方案，可以使系统频率在故障后更快地恢复稳定，能够提高电网孤岛运行的稳定水平。

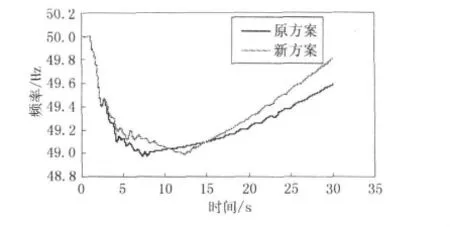
图5 2种频率协调控制方案的对比

4 结束语

本文建立了频率稳定分析的动态数学模型，考虑发电机调速器模型和负荷频率调节系数对频率的综合影响，以实际电网中的孤岛系统为研究对象进行仿真分析，提出了一种新的孤岛频率协调控制方案。仿真结果证明了该控制方法的可行性，能够增强低频减载装置适应系统变化的能力，并实现对减载量的准确控制。

［1］ 袁季修．防止电力系统频率崩溃的紧急控制 ［J］．电力自动化设备，2002，22(4):1－4．

［2］ Liu Guoping，Xu Zheng，Huang Ying，etal．Analysis of interarea oscillation in the south china interconnected power system［J］．Electric Power System Research，2004，70(1):38 －45．

［3］ 王铁强，贺仁睦，王卫国，等．电力系统低频振荡机理的研究［J］．中国电机工程学报，2002，22(2):21－25．

［4］ 黄 莹，徐 政，曾德文，等．东北、华北和华东电网联网方案研究［J］．电网技术，2005，29(1):1－6．

［5］ 王 葵，潘贞存．一种新型低频减载方案的研究 ［J］．电网技术，2001，25(12):32－33．

［6］ 庄侃沁，武 寒，黄志龙，等．龙政直流双极闭锁事故华东电网频率特性分析 ［J］，电力系统自动化，2006，30(22):102－104．

［7］ 陈俊山，洪兰秀，郑志远．电力系统低频减载研究与应用发展 ［J］．继电器，2007，35(14):79－82．

［8］ 秦明亮，杨秀朝．减少低频减载方案过切的措施研究 ［J］，电网技术，2002，26(3):84－86．

［9］ 熊小伏，周永忠，周家启．计及负荷频率特性的低频减载方案研究［J］，中国电机工程学报，2005，25(19):49－51．

［10］ DL428—91．电力系统自动化低频减负荷技术规定 ［S］．