基于有限元理论的路面加铺层结构设计方法研究

赵 丽

（邯郸市高速公路管理处，河北 邯郸 056000）

沥青路面补强设计普遍采用的是弹性层状体系理论。弹性层状体系理论主要的缺点是假设每一层材料都各向同性且为线弹性。由于这一假定，难以对非线性材料组成的层状体系（如未处理的粒料基层和底基层）进行分析。这些材料的弹性模量值随应力改变，而且在层体中也是不等的。随之产生的问题是：用非线性层中的哪一点来代表这一层？按通常的路面设计方法，只需知道最不利的应力、应变和挠度，则选择靠近荷载作用点便是合理的[1]。然而，假如希望知道某些靠近荷载作用点又要知道某些远离荷载作用点处的应力、应变和挠度，就难以应用弹性层状理论来分析非线性材料。应用有限元法则可以克服这一缺陷。

1 有限元法概述

1.1 基本理论

有限元法的基本思想是将连续的结构离散成有限个单元，并在每一个单元中设定有限个节点，将连续体看作是只在节点处相连接的一组单元的集合体；同时选定场函数的节点值作为基本未知量，并在每一个单元中假设一个近似插值函数以表示单元中场函数的分布规律；进而利用力学中的某些变分原理去建立用以求解节点未知量的有限元法方程，从而将一个连续域中的无限自由度问题转化为离散域中的有限自由度问题。一经求解就可以利用解得的节点值和设定的插值函数确定单元上以至整个集合体上的场函数。

1.2 基本假设

有限元法的基本假设有三个：

a）荷载作用形式为圆形均布荷载；

b）圆形均布荷载的直径远远小于路面的宽度；

c）路面内部应力分布呈轴对称，即对称于荷载轴心线。

2 计算说明

2.1 建立有限元模型

根据轴对称空间问题的有限单元法的基本假设，可以用两种方法建立模型。方法一：平面4节点轴对称模型；方法二：20节点3维6面体模型。由于对于空间轴对称问题来说，方法二不但建模繁琐、计算耗时过长，而且精度并不比方法一高，如果不考虑材料的特殊性质时，不推荐采用方法二。因此本文只利用方法一进行建模。

建立平面4节点轴对称模型时假定：距离荷载作用点一定的水平和垂直距离外结构内的应力和位移可以近似为0，此处边界上的自由度可以认为全部为0。下卧层材料的破损以及材料的各相异性、粘弹性本构等相关参数难以确定。模型的材料参数为：加铺层厚度为8cm，弹性模量为1 200MPa，泊松系数为0.25；下卧层弹性模量为256MPa，泊松系数为0.3。模型分双层，下层取路基全宽即上顶宽度为10m，厚度为5m；上层为8cm×10cm矩形模型。

由于加铺层是摊铺在旧沥青路面上的，所以层间条件应该视为完全连续，不应该为光滑或半光滑[2]。新建公路沥青路面之所以不能把层间条件视为完全连续是因为面层和基层材料的截然不同，无法结合紧密，所以层间条件必然处于光滑与连续之间。而加铺层材料与旧路面的材料是相同的，施工时旧路面相当厚的部分中的沥青会在加铺层材料的高温下熔化，并与加铺层紧密结合，因此视为完全连续是合理的。构造的有限元模型见图1。A1为加铺层部分，A2为下卧层部分。

图1 有限元模型

2.2 定义边界条件及荷载

根据前文的假定，模型的边界条件为：DOF＝0，即自由度为0。这样的假设基于以下考虑：利用布辛尼斯克解可以求得在BZZ-100作用下，土基的影响区深度为150cm左右，即行车荷载作用对于深度大于150cm处土基的影响可以忽略。此处模型的总高度为508cm，远远大于150cm，所以其自由度可以视为0。水平方向的路面宽度取1 000cm则是完全模拟半幅路面宽度。边界条件及荷载布置见图2。

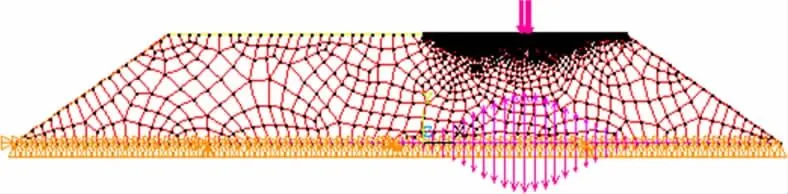
图2 有限单元边界条件

3 结果分析

3.1 应力分析

根据前文给出的材料参数、边界条件及荷载条件，可以得出模型内部不同单元的应力和应变，并生成应力等值线图和矢量图。图3为拉应力分布等值线图。

图3 拉应力分布等值线图（局部放大）

从弯拉应力等值线图中不难发现，在分析模型中，拉应力分布不连续。最大弯拉应力点为C、D两点，正是加铺层底面行车荷载作用处，最大拉应力值为0.21MPa。加铺层层表A、B点同样也承受拉应力，但是其值小于C、D两点的值，为0.143MPa。有限元法得出的这种规律与弹性层状体系所得出的规律是相同的，但是结果偏小。在下卧层中弯拉应力都接近于0，没有应力集中点。

为了更直观地反映加铺层表面及底面应力的分布情况，对行车荷载作用面下的加铺层表及层底的应力绘制了路径图（见图4、图5）。

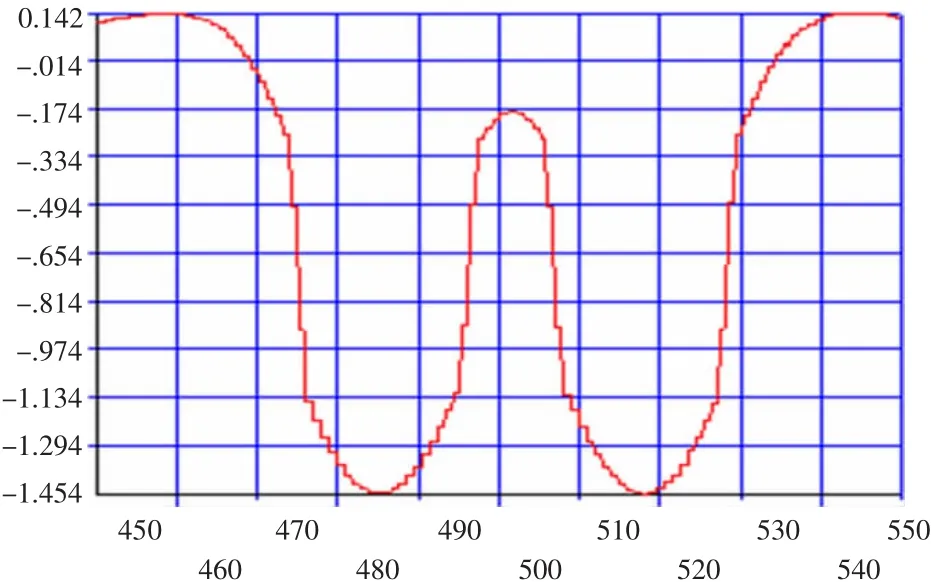
图4 加铺层表面弯拉应力分布

图5 加铺层底面弯拉应力分布

从图4与图5可以看出，层表最大弯拉应力值为0.143MPa，小于层底最大弯拉应力0.21MPa。这说明在这次计算中所设定的条件下计算路面厚度，考虑材料弯拉应力时首先要考虑加铺层底面C、D点的弯拉应力是否能满足材料要求。

第1主应力为单元上的最大拉应力。图6表明结构层中最大第1主应力的分布与弯拉应力的分布是相似的。最大第1主应力位于均布荷载作用面下加铺层底。此处最大第1主应力为0.211MPa，与结构层中的最大弯拉应力0.21MPa近似相等。因此选取最大弯拉应力作为验算应力是合适的。

图6 第1主应力分布等值线图（局部放大）

第3主应力是最小的主应力，即单元体所受到的最大压应力。第2主应力是介于第1主应力与第3主应力之间的应力值。在平面应变问题中第3主应力的分布等值线图与垂直应力分布等值线图相似，即最大应力都发生在加铺层表面荷载作用点处。最大第3主应力σ3＝-1.453MPa，大于最大垂直应力σy＝-0.7MPa。

同时，在有限元计算结果中可以发现，在荷载作用面下一定范围内，单元垂直位移的趋势最为明显。在远离荷载的加铺层表面，单元有向上和向外侧移动的趋势。这一点可以很好地解释路面上车辙形成的原因。并且，在结构层上部的加铺层中第1主应力较大，且以荷载作用面下最为集中。荷载作用面下的加铺层和下卧层相当厚的部分中第3主应力较大。通过分析已经知道，第1主应力为拉应力，其余的两个主应力则为压应力，因此可以肯定的是：加铺层主要承受因行车荷载作用而产生的拉应力，而下卧层则承受压应力多一些。所以，在选择加铺层材料时，要求该材料的抗拉模量一定要大。目前增大加铺层抗拉能力的方法之一就是在层中或者层间加铺玻纤格栅。

3.2 加铺层厚度的确定

当行车荷载的大小、累积作用次数以及材料参数一定时，随着加铺层厚度的变化，结构层内的应力、应变也都随之发生变化。因此必定存在最合理的加铺层厚度[3]。沥青混合料的抗拉模量远远小于其抗压模量，但是从结构层内应力情况来看，最大拉应力与最大压应力相差并不大。在本文计算中，最大压应力为0.7MPa，而最大拉应力也接近于0.2MPa。这表明用最大拉应力作为控制加铺层厚度的主要指标是很合适的。而且从结构层中的主应力矢量图中也可以看出，加铺层承受的第1主应力要远大于其他两个主应力。

为了验证最大拉应力位置和大小随层厚变化的规律，对不同加铺层厚度下最大拉应力发生的位置和大小进行了计算（见图7）。图中A、B、C、D、E是最大拉应力发生的不同位置的代号。

图7 拉应力随加铺层厚度变化曲线

图7 表明，层表A、B点的拉应力随层厚几乎没有发生变化，层表轮隙E点处的拉应力则随加铺层厚度的增大而减小，从受拉状态变为受压状态。当加铺层厚度较薄（小于5cm）时，层底C、D点承受压应力。当加铺层大于5cm时，层底C、D点承受拉应力，其值随加铺层厚度的增大而缓慢增大。当加铺层厚度等于9cm时，层底C、D点所受到的拉应力达到峰值。当加铺层厚度小于6cm时，层表A、B点所受到拉应力大于层底C、D点的拉应力，此时进行路面设计时应该采用A、B点的应力作为控制。当加铺层厚度大于6cm时，C、D点应力大于A、B点，所以进行加铺层厚度设计时，应以C、D点的应力作为控制。

4 结论

综合上述分析，有以下三点主要结论：

a）有限元设计方法能根据具体情况建立与实际比较符合的模型，而且能较好地模拟车辆荷载作用下的沥青加铺层内以及下卧层中的荷载响应；

b）应选择抗拉模量大的材料作为加铺层材料，目前增大加铺层抗拉能力的方法之一就是在层中或者层间加铺玻纤格栅；

c）宜采用最大拉应力作为控制加铺层厚度的主要指标。

[1]李炜，王朝晖.沥青路面加铺层补强设计结构方案优化分析[J].吉林交通科技，2010，（1）：13-15.

[2]陈峙峰.旧水泥混凝土路面补强设计方法研究[J].河南科学，2004， （5）： 669-672.

[3]王飞跃，王奎生.旧路面的补强利用与拆除重建方案分析[J].黄河水利职业技术学院学报，2002，（7）： 40-43.