多液压缸控制系统的同步设计

王桂荣，刘芳璇，许宏，陈锡爱

(中国计量学院机电工程学院，浙江杭州310018)

在液压缸同步控制系统设计中，系统输出响应要求具有较高稳定性和控制精度。为了提升系统的动态性能指标，常采用PID 闭环控制。而传统的PID控制虽然算法简单，鲁棒性好，可靠性高，但对于非线性、变负载、时变的复杂系统存在不能在线调整的缺陷[1]，因此，多采用算法优化PID参数，如采用BP神经网络优化PID参数[2]，或采用模糊控制及自适应控制等抑制非线性时变干扰[3－6]。目前常用的同步控制策略有交叉耦合、电子虚拟主轴等，交叉耦合不适用于两个以上对象的控制，电子虚拟主轴在系统启停时同步控制精度较差。

作者介绍了一种串级液压缸控制系统的设计与实现，采用速度－电压、位移－摆角、位移－电压三闭环控制，对液压控制系统中的泵控缸位移开环控制环节予以改进，以提高控制稳定性和精度。在研究多个不同参数的液压缸控制系统的同步性能时，采用偏差耦合控制策略，并对每个阀控缸、泵控缸的控制参数采用自适应遗传算法进行优化。由仿真结果可知，优化控制后的液压缸系统具有良好的抗干扰性和同步控制精度，对阶跃信号响应快速，无超调，并能够对斜坡信号、正弦信号无偏跟踪。

1 泵控液压缸的数学模型

下面分别以阀控缸、泵控缸为例，建立并分析液压泵控系统的数学模型，假定:

(1)液压系统在正常状态下工作，液压泵的角速度是恒定的。

(2)管道中液流为层流，有沿程阻力损失。

(3)液压泵和液压马达没有流量脉动，可忽略补油压力。

1.1 泵控缸的传递函数

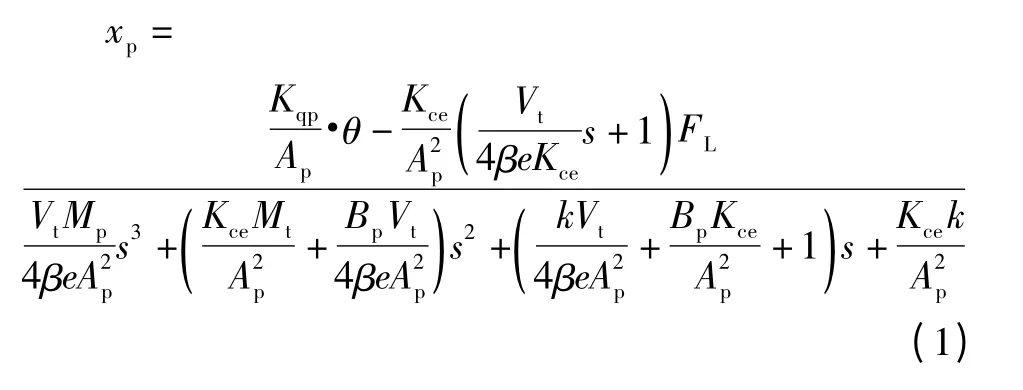
式中:Kqp为变量泵流量增益，Kqp=Kce·ηp，ηp为变量泵叶片转速;θ为变量泵摆角;Vt为泵控缸等效总体积;Ap为活塞面积;xp为活塞位移;Mt为活塞及由负载折算至活塞上的总质量;Bp为活塞及负载等运动件的黏性摩擦系数;βe为油液及管道体积的弹性模量;k为负载运动时的弹性负载刚度;FL为外界干扰力矩;Kce为总泄漏系数。

1.2 阀控缸的传递函数

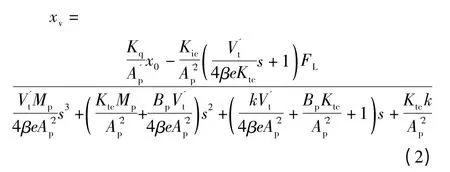
式中:Kq为比例阀的流量增益;xv为比例阀方向阀阀芯位移;Kic为阀控液压缸的内泄漏系数;Ktc为阀控液压缸的总泄漏系数;A'p为缸活塞作用面积;为进、回油腔总体积;Mp为变量缸活塞及1/3 两只对中弹簧质量和;Bp为变量缸活塞和负载的黏性阻尼系数;βe 油液及管道体积弹性模量;k为变量缸对中弹簧和负载刚度;FL为外界干扰力矩。

考虑到负载黏滞摩擦系数Bp较小，设kh=是把封闭油液看成弹簧时的液压弹簧刚度。一般情况下故可略去项。则式(1)、(2)可近似等价为如下的三阶积分加振荡环节，即:

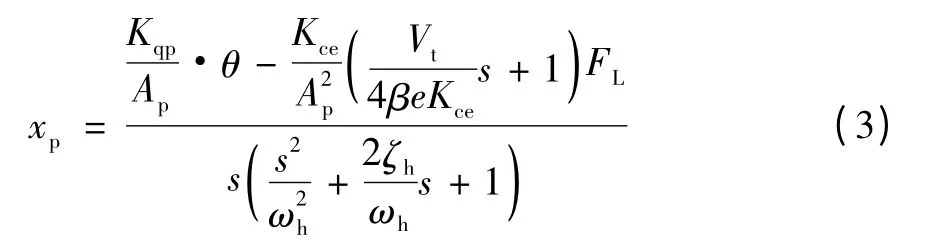
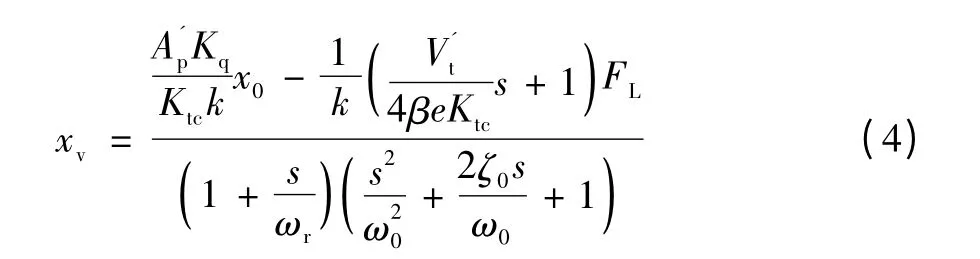
文中在假设阀控缸无扰动的前提下，采用对单组液压缸的速度－电压、位移－摆角、位移－电压三闭环PID控制方案。其控制系统结构如图1所示。

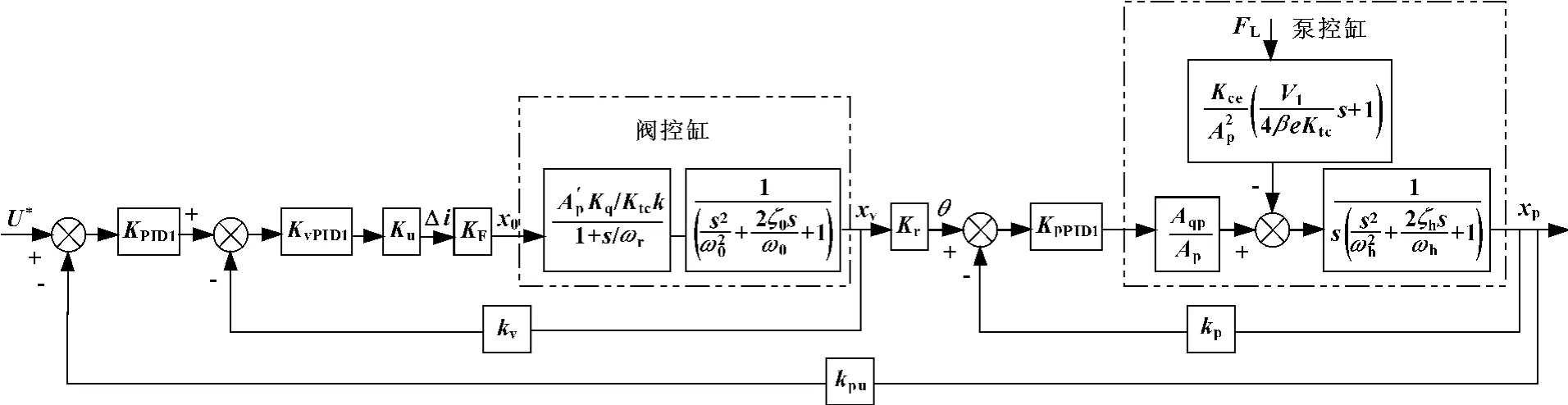
图1 单对象控制系统结构图

图中，U*为输入的参考电压，kF为电流比例阀位移增益，kr为比例阀增益，ku为电流对电压的增益，kv为速度对电压的反馈，kp为位置对变量泵斜盘角的反馈，kpu为位置对电压的反馈。x0为电流阀位移，Δi为电流增量，存在关系为:x0=kFΔi。

2 自适应遗传算法的实现

遗传算法(Genetic Algorithm，GA)是建立在自然选择和自然遗传学机制基础上的迭代式全局优化概率搜索算法[7－8]。

文中采用自适应的遗传算法对速度－电压、位移－摆角、位移－电压三闭环的控制参数进行优化。在优化算法中加入了滤波小组，以减少初始参数选择的盲目性，降低了初始局部收敛的概率;采用半扫描筛选方式筛选初始种群，以防止加大比例系数引起超调量的增加;采用联赛法进行选择操作，最优基因不通过选择，直接参加下一次进化，并替换种群中最差个体的方式以减小在挑选个体时的随机性。构造动态自适应交叉概率Pc与变异概率Pm，并辅以精英策略和保优运算，自适应地调整种群的Pc和Pm。为获取满意的过渡过程动态特性，采用误差绝对值时间积分性能指标 (ITAE)作为参数选择最小目标函数。在目标函数中加入控制输入的平方项，并引入惩罚机制。选用式 (5)作为参数选择的最优指标:

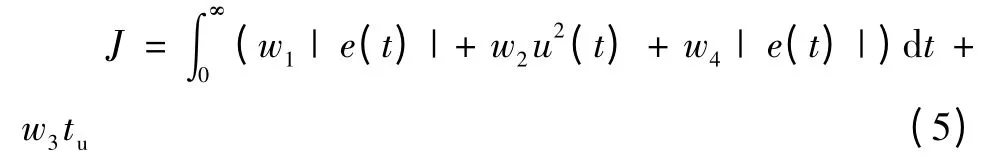
式中:e(t)为系统误差;u(t)为控制器输出;tu为上升时间;w1，w2，w3，w4为加权值。

3 三液压缸同步控制模型

文中采用偏差耦合控制策略对多泵系统的同步性能进行研究。偏差耦合的主要思想是将某一台液压缸的活塞位移反馈同其他液压缸的活塞位移反馈分别作差，然后将位移差值作为相邻两个液压缸的补偿信号。由于偏差耦合同步控制策略把所有回路之间的差值均作为彼此的补偿信号，因此，任何一个回路出现位移波动或负载变化，其他回路输出都能保证对输入信号很好地跟随，故偏差耦合控制能够实现很好的同步性能。

选取三组参数互不相同的液压缸，依据偏差耦合控制策略，采用PID控制器对活塞位移反馈量的差值进行调节，对三闭环系统进行扰动补偿。其控制系统结构如图2所示，虚线部分的结构如图1所示。

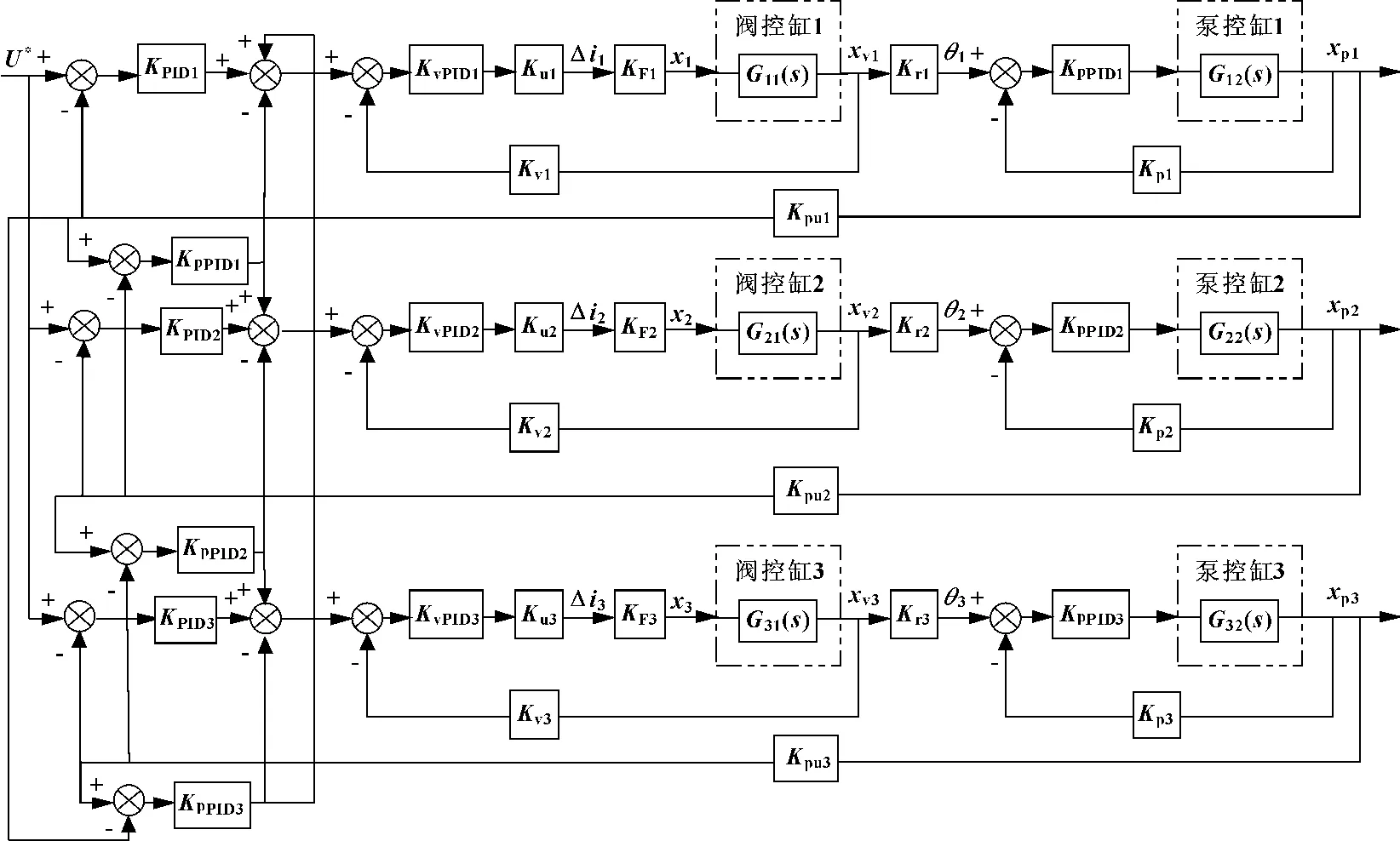
图2 偏差耦合同步控制系统结构图

4 仿真分析

为验证同步控制模型的控制效果，针对液压缸电液伺服系统进行了仿真研究。选取泵控缸、阀控缸的控制参数如表1、2所示。

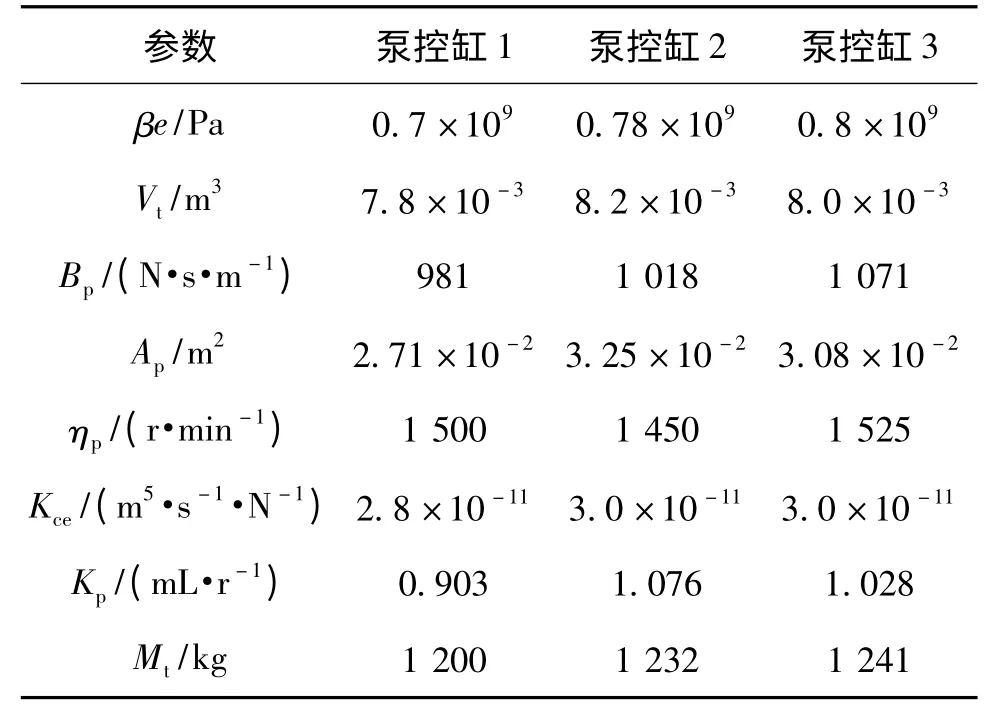
表1 泵控缸参数

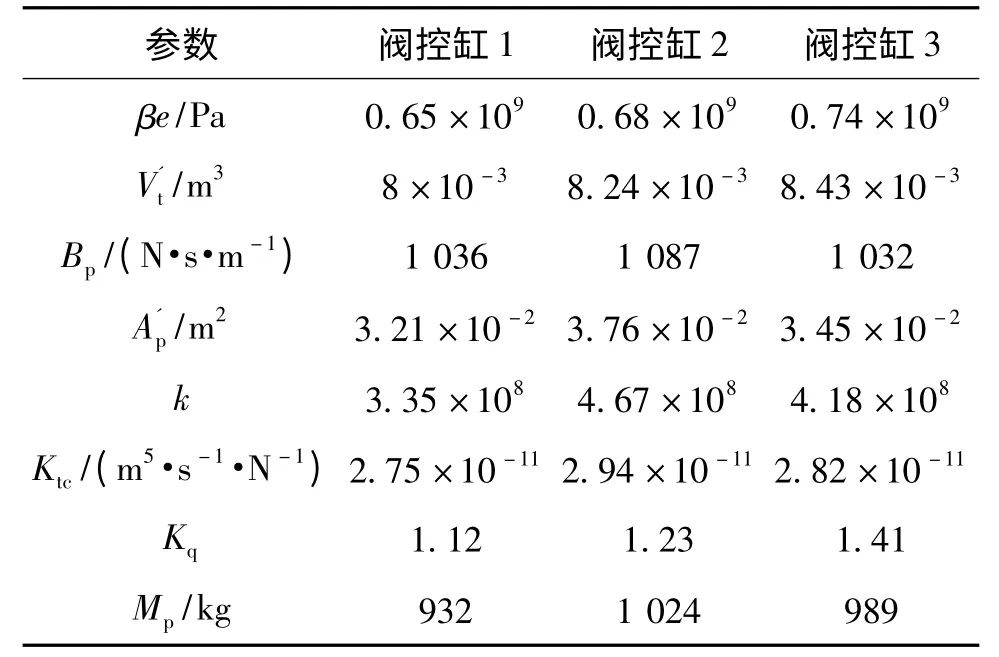
表2 阀控缸参数

取第一组液压缸参数进行仿真，对阀控缸位移－参考电压、泵控缸位移－摆角、泵控缸位移－参考电压三闭环系统分别采用临界比例度法和自适应遗传算法对其PID控制参数进行整定优化，其结果见表3。在单位阶跃信号作用下，系统阶跃响应曲线如图3所示。

表3 两种参数优化方法的结果比较

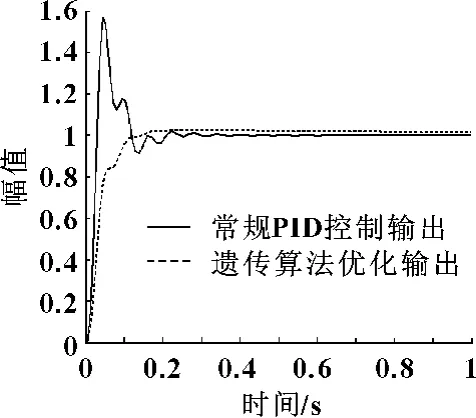
图3 阶跃信号响应仿真曲线

对三组液压缸的每个闭环PID控制器均采用自适应遗传算法优化，并在15 s时引入幅值为15的阶跃扰动，取适当的位置反馈PID控制参数对系统进行扰动补偿，在偏差耦合同步控制策略下得系统对单位阶跃、单位斜坡以及幅值为1，频率为0.5的正弦输入信号的跟踪响应曲线如图4所示。

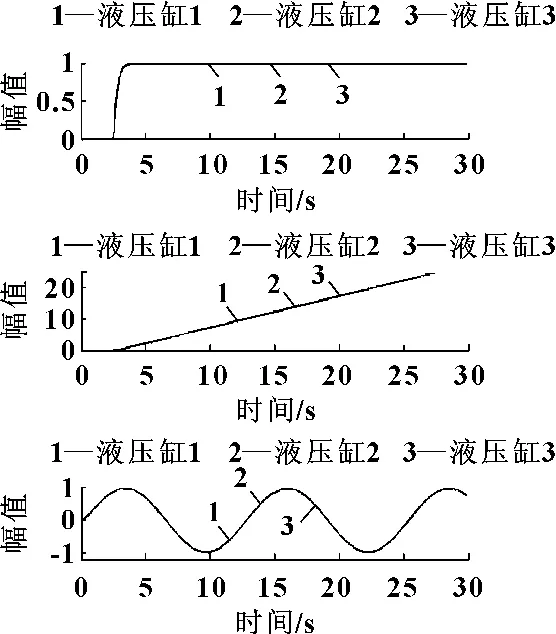
图4 3种输入信号下系统的跟踪响应曲线

由图4可知，系统在单位阶跃信号作用下，系统能够迅速达到稳态(0.95 s)，且无超调量，抗扰动性能较好(1.3 s 恢复稳态)。在单位斜坡信号和正弦输入信号作用下，系统能够对输入信号实现无偏跟踪，响应较快，鲁棒性好。

5 结束语

在液压泵控缸系统的设计中，考虑到液压缸组的参数互不相同，提出在偏差耦合控制方式下采用自适应遗传算法对输出反馈量进行调节的同步控制方案。经过对仿真曲线的分析比较，得知采用基于遗传算法的偏差耦合控制策略时，系统阶跃响应无超调，响应迅速，稳态精度高，上升和调整时间短，抗扰动能力强;对斜坡信号、正弦信号能够实现无偏跟踪。

【1】肖理庆，邵晓根，张亮，等.利用改进遗传算法优化PID参数[J].计算机工程与应用，2010，46(1):200－202.

【2】高强，金勇，王力，等.泵控缸电液位置伺服系统建模研究[J].兵工学报，2011(8):950－956.

【3】刘礼华，戴长秋，黄元峰.基于变频技术的泵控缸液压调速系统的模糊PID控制的仿真研究[J].机械与电子，2011(9):69－72.

【4】张红娟，权龙，程衍.永磁同步电动机驱动泵控缸系统抗扰研究[J].中国电机工程学报，2010(11):84－89.

【5】高强，侯远龙，钱林芳.泵控缸电液位置伺服系统的自适应模糊滑模控制[J].机床与液压，2007(12):94－96.

【6】王洪斌，张永顺，冯少婵，等.直驱泵控缸系统建模及自适应反推滑模控制[J].电机与控制学报，2011(9):92－98.

【7】WANG Y P，WATSON N R，CHONG H H.Modified Genetic Algorithm Approach to Design of an Optimal PID Controller for AC-DC Transmission Systems [J].Electrical Power and Energy Systems，2002(24):59－69.

【8】SZETO K Y，ZHAO S Y.Adaptive Spatial Allocation of Resource for Parallel Genetical Algorithm[J].Studies in Computational Intelligence，2008，129(5):389－398.