三通阀控单作用缸电液伺服系统的建模与仿真

阎晓珊，刘玉绒

(1.东北电力大学机械工程学院，吉林吉林132012;2.广州机械科学研究院有限公司，广东广州510700)

在液压伺服系统中，采用控制液压系统的压力从而控制系统的输出力的形式较为普遍。例如精轧机正弯辊液压系统，对液压缸加载时的弯辊输出力的精度和稳定性要求精确控制，但对卸载时的力要求并不高。若采用对称缸，则实物结构尺寸大，对结构尺寸要求严格的设备并不适合;而采用对称四通阀控制不对称缸在运动换向的瞬间存在巨大的压力跃变，这对压力控制是极其不利的[1]。针对这种特殊要求的场合，可以采用标准的四通伺服阀堵死一个控制口不用，使伺服缸无杆腔受控，而活塞杆腔通入恒定的低压，这样就相当于三通阀控单作用缸，如图1所示[2]。

活塞杆腔通入的低压恒压，作用是防止活塞杆腔空吸并吸入灰尘，同时也起到增加阻尼的作用。液压系统简化后如图1所示[3]。

由于这种三通阀控单作用缸受控腔只有无杆腔，在压力控制过程中，若有外力干扰(如精轧机咬钢和抛钢)时，会使无杆腔压力上升和下降，则三通阀控单作用缸通过控制伺服阀阀芯的向左或向右位移，继而控制压力油流入或流出伺服缸无杆腔，相应地调整受控腔的压力，使受控压力迅速恢复到设定值。

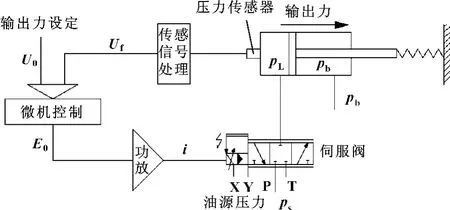
图1 液压系统简化图

1 建立电液伺服系统数学模型

1.1 液压动力机构

文中所讨论的对象是三通阀控单作用缸电液伺服系统，它可看作只有惯性负载和阻尼的动力机构，其动力机构示意图如图2[4]。

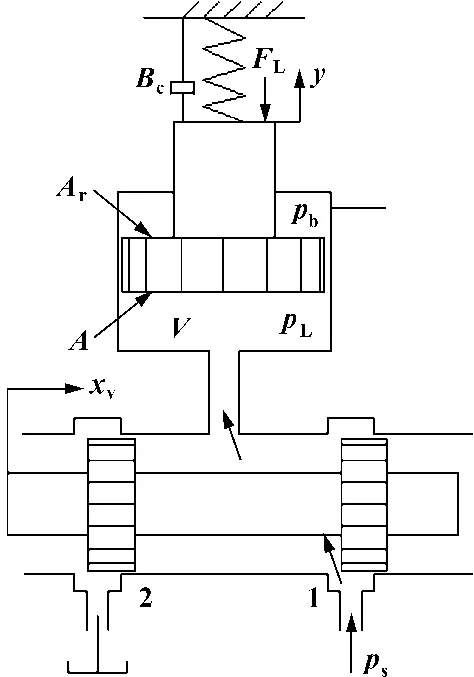
图2 动力机构示意图

图中各参数的含义如下:

y为活塞杆的位移，m;

Bc为活塞和负载的黏性阻尼系数，N/(m/s);

FL为外负载力，N;

m为活塞和负载的总折算质量，kg;

A为液压缸无杆腔的有效面积，m2;

Ar为液压缸有杆腔的有效面积，m2;

ps为供油压力，Pa;

pL为负载压力，Pa;

pb为液压缸背压腔油压(为定值)，Pa;

xv为滑阀阀芯位移，m;

V为所取控制腔的体积，m3。

由于系统对液压缸加载时的输出力要求进行精确控制，而对卸载时的输出力控制要求并不高，因此这里主要讨论xv≥0 加载状态时的特性[5－7]。

(1)伺服阀基本方程

式中:Kc0为流量压力增益，m5/(N·s);

Kq0为流量增益，m2/s，

qL为伺服阀负载流量，m3/s。

(2)液压缸流量的连续性方程

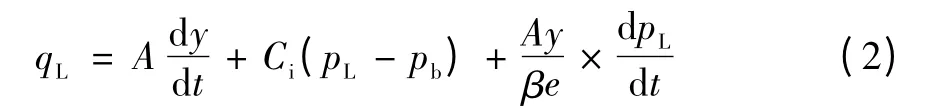
由于液压系统在稳定工作时，液压缸的位移变化量很小，因此可将Ay 视作常数V0，则

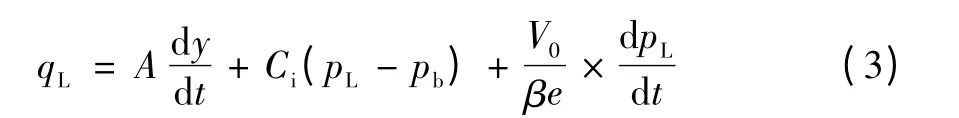
(3)液压缸和负载的力平衡方程

忽略库仑摩擦等非线性负载，忽略油液的质量，根据牛顿第二运动定律，可得

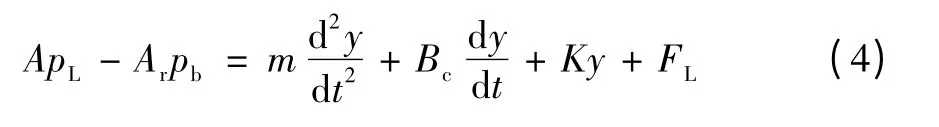
式中:Bc为活塞和负载的黏性阻尼系数，N/(m/s);

K为负载的弹簧刚度，N/m。

(4)三通阀控单作用缸压力系统的输出方程

将式(1)、(3)、(4)拉氏变换得

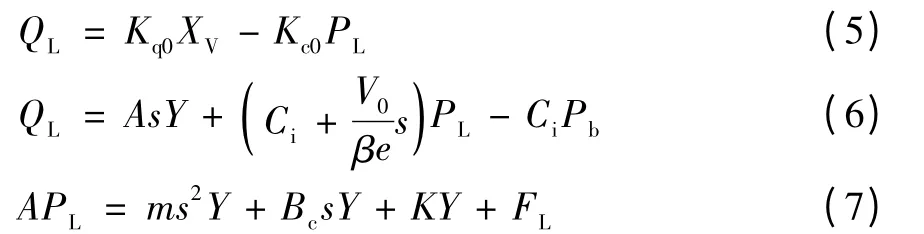
由式(5)、(6)、(7)可以求得

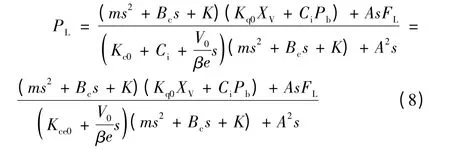
式中:pL为液压缸压力输出，Pa;

Kce0为总的流量－压力系数，m5/(N·s);

Ci为液压缸的内泄系数，m5/(N·s);

V0为液压缸工作腔的容积，m3;

βe为液体体积弹性模数，Pa;

FL为外负载力，N;

m为活塞和负载的总折算质量，kg;

Bc为活塞和负载的黏性阻尼系数，N/(m/s);

K为负载的弹簧刚度，N/m。

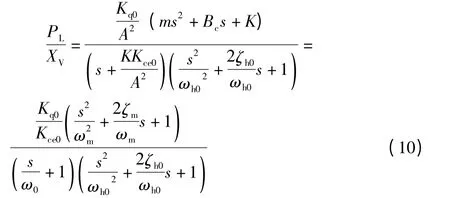
式中:ω0为惯性环节的转折频率，rad/s;

ωm为负载的固有频率，rad/s;

ζm为负载的阻尼比;

ωh0为液压弹簧和负载弹簧与质量构成的系统固有频率，rad/s;

ζh0为液压弹簧和负载弹簧与质量构成的系统阻尼比。

1.2 伺服阀传递函数

工程中使用的伺服阀的传递函数通常有如下形式:

式中:Ksv为伺服阀的流量增益，(m3/s)/A;

ωsv为伺服阀的固有频率，rad/s;

ζsv为伺服阀的阻尼比。

1.3 伺服放大器的传递函数

伺服放大器的固有频率一般远远高于动力机构及伺服阀的固有频率，可以当作比例环节，即

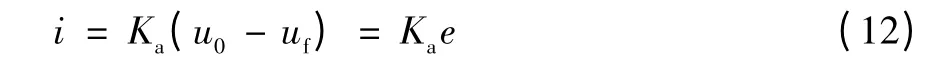
拉氏变换为

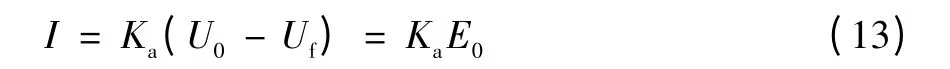
式中:i为放大器输出电流，A;

Ka为放大器增益，A/V;

u0为弯辊力给定电压信号，V;

uf为压力传感器输出的油压反馈信号，V;

E0为偏差信号，V。

1.4 压力传感器

压力传感器在系统中也视为比例环节

式中:Uf为压力传感器输出电压，V;

Kf为压力传感器的变换系数，V/Pa;

pL为伺服阀工作压力，Pa。

1.5 系统方框图及传递函数

当不考虑管路动特性时，可以由上面各式得出加载xv≥0时压力闭环传递函数的方块图，并写出系统的开环传递函数。

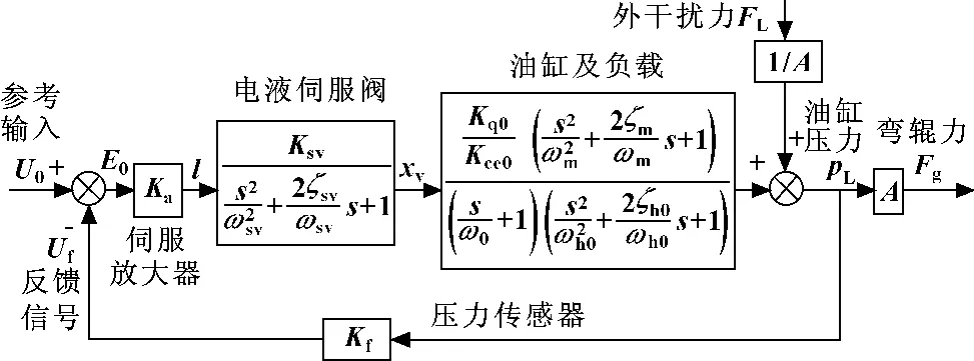
图3 压力闭环系统方框图

系统的开环传递函数G0(s)为

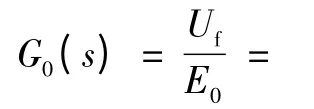
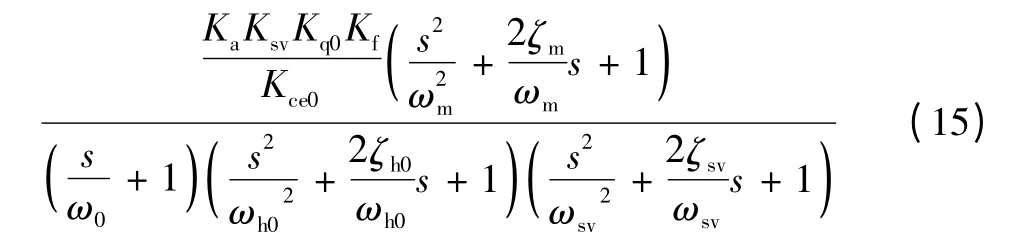
2 仿真试验

采用MATLAB软件对控制系统进行仿真[8－10]，以控制精轧机液压弯辊1 500 kN为例进行加载状态的仿真，分别获得如下仿真框图、系统开环Bode图、系统压力阶跃响应和输出力仿真图如图4—8所示。

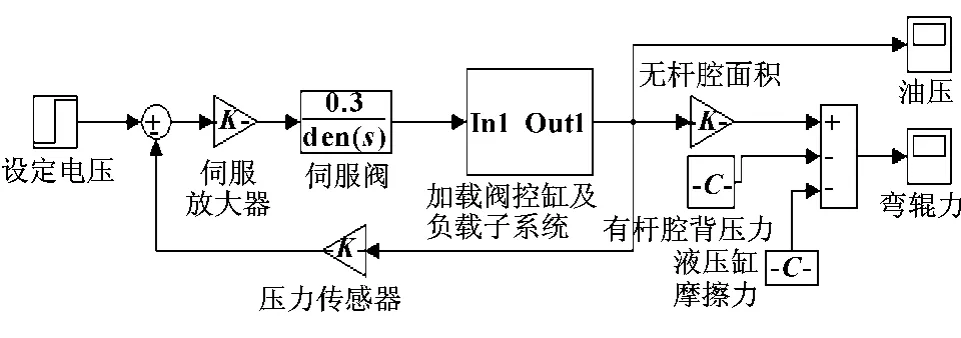
图4 压力控制系统仿真框图

图5 阀控缸及负载子系统

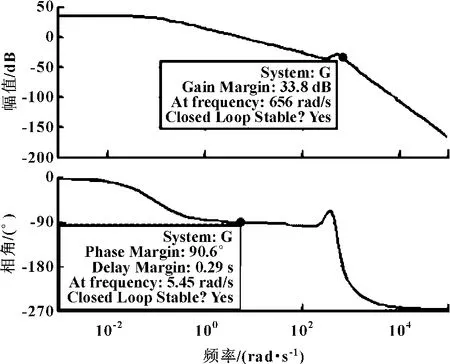
图6 系统开环伯德图

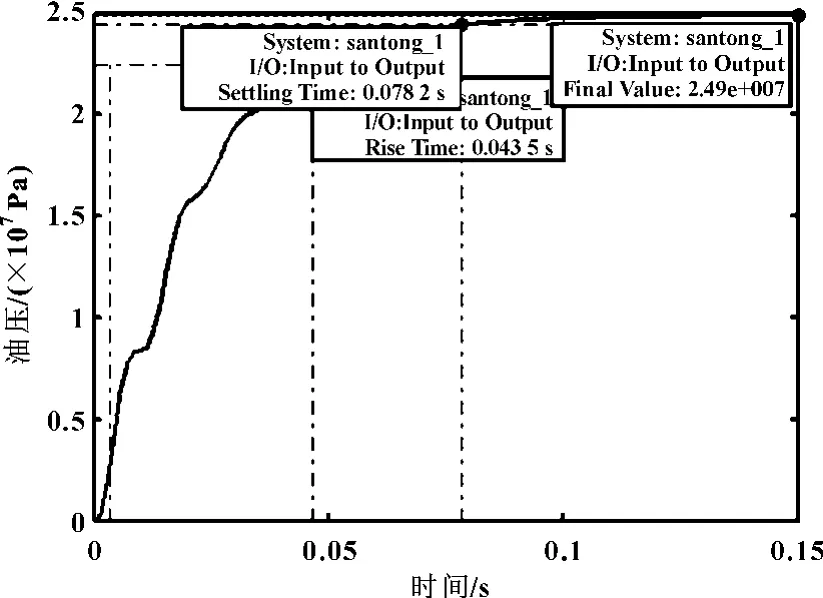
图7 系统压力阶跃响应

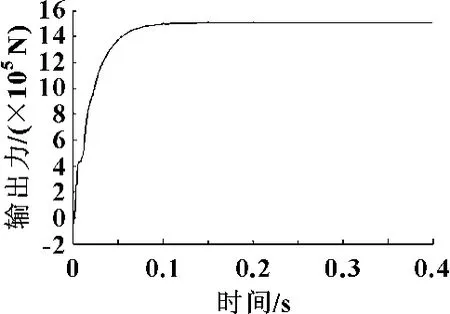
图8 输出力仿真图

从系统开环Bode 图图6中可知，其幅值稳定裕量Kg为33.8 dB，相位稳定裕量γ=90.6°，系统是稳定的。

从系统压力阶跃响应图7中可知，系统上升时间为0.043 5 s，到达稳定时间约为0.078 2 s，响应较快。稳态误差是系统实际输出的油压和给定的油压之差，即e－ss=Δp=4.2×105Pa，其超调量为1.68%。由图8看出，仿真图中输出力15×105N与系统本身要求的弯辊力1 500 kN是一致的。

3 主要参数对系统动态特性的影响及优化

分别变动一些主要参数进行仿真(图9)，观察系统动态特性发生的变化，并给出相应的优化措施[11]。

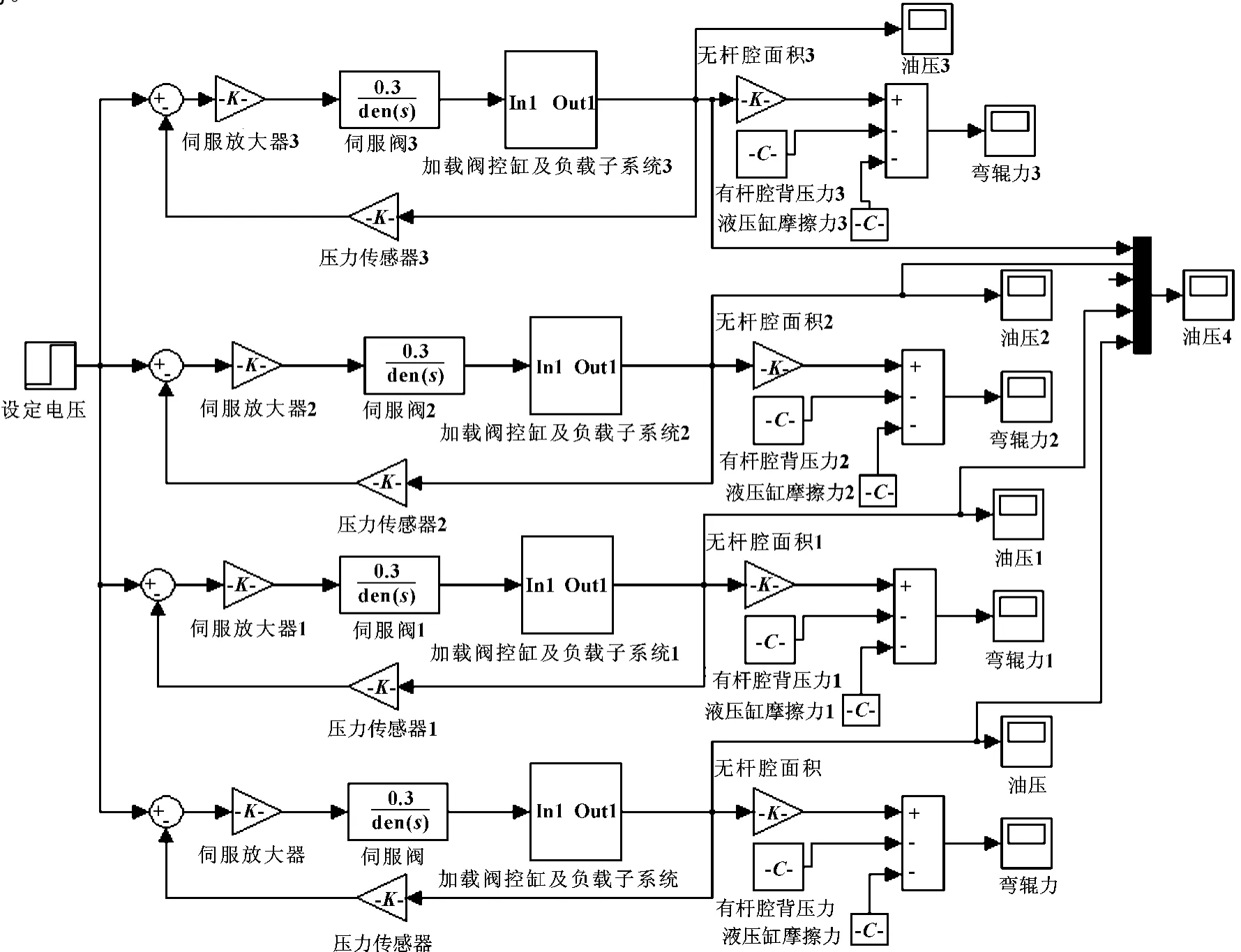
图9 改变主要参数的系统仿真框图

(1)随着伺服放大系数Ka的增大，响应时间越来越快，但当增大到一定程度后，对响应时间的影响将变小。所以放大系统要在一个有效的范围里选择，才能保证系统的可靠性;(2)随着液压缸高压腔容积的减少，系统的快速性有所增加，但系统的稳定性变化不太明显。所以在选择管路时应尽量考虑管路的走向;(3)随着负载弹性刚度的增加，系统的快速性有所增加，但系统的稳定性变化不太明显。如果负载弹性刚度过大，对系统的快速性起不了多大作用。

4 结论

所建立的模型能体现原系统的主要特征，简化较为合理。利用MATLAB软件SIMULINK 进行的仿真分析，能较好地复现实际系统的输出。改变系统主要参数并观察其对系统的影响，由此给出优化措施对实际设计具有指导意义。由于液压伺服系统中包含很多非线性因素，今后应在非线性补偿方面作一些深入研究。

【1】田文波.液压弯辊控制系统的仿真与优化[D].重庆:重庆大学，2005.

【2】成大先.液压控制[M].北京:化学工业出版社，2004:83－155.

【3】曹鑫铭.液压伺服系统[M].北京:冶金工业出版社，1991:225.

【4】王传礼，丁凡，李其朋.对称四通阀控非对称液压缸伺服系统动态特性研究[J].中国机械工程，2004(6):471－474.

【5】纪群，王京，郭强.连轧粗轧机AWC 液压位置控制系统的建模研究[J].机床与液压，2007，35(12):111－113.

【6】孟亚东，李长春，张金英，等.阀控非对称缸液压系统建模研究[J].北京交通大学学报，2009，33(1):66－77.

【7】李阁强，王爱花，谢海良.阀控非对称缸被动加载系统数学模型的建立[J].机床与液压，2009，37(8):78－80.

【8】李永堂，雷步芳，高雨茁.液压系统建模与仿真[M].北京:冶金工业出版社，2003:199－210.

【9】吴振顺.液压系统仿真与CAD[M].哈尔滨:哈尔滨工业大学出版社，2000:41－74.

【10】薛定宇.控制系统仿真与计算机辅助设计[M].北京:机械工业出版社，2005:152－182.

【11】胡良谋，李景超，曹克强.基于MATLAB SIMULINK的电液伺服控制系统的建模与仿真研究[J].机床与液压，2003(3):230－231.