基于改进CSA-蒙哥马利的RSA加密处理器实现
王开宇,唐祯安,赵 赟,周煜迪
(大连理工大学 电子信息与电气工程学部,辽宁 大连 116024)
0 引 言
随着信息化时代的不断推进,电子商务、电子通信等诸多领域的信息安全受到越来越多的关注.为了保护电子信息,各种加密算法被应用在信息安全中.其中应用较广泛的RSA 加密算法,是一种非对称加密算法,即加密密钥和解密密钥是分开的.RSA 在FPGA 上的实现主要是利用蒙哥马利算法将求幂取余运算转换成硬件上容易实现的移位和相加运算,本文对算法结构做一些改进,以降低器件资源的使用,提高算法速度,最终在FPGA 上实现并进行验证.
1 RSA 算法原理介绍
RSA 是以Rivest、Shamir、Ad-leman这3位提出者的名字而命名的.其安全性主要是依靠大数的难以分解性质.
首先,选择两个大素数P、Q,计算N=P×Q,然后选择一个非(P-1)和(Q-1)因子的公钥E,通过(D×E)mod(P-1)(Q-1)=1,得出私钥D.设明文为A,密文为B,则加密过程为B=AEmodN,相似地,解密过程为A=BDmodN.由此可见,加密和解密运算都是求幂取余,当数很大时,如果直接计算幂再取余,无论在硬件还是软件上实现都是不可能的.蒙哥马利算法正是将其转化成移位和相加并且幂和取余运算同时进行,利于在硬件上实现.
2 蒙哥马利算法及其改进
蒙哥马利算法的基本思想是通过移位和相加来实现模乘运算,文献[1-2]中对蒙哥马利算法做了些改进,改进后的算法如下:
算法1

算法2
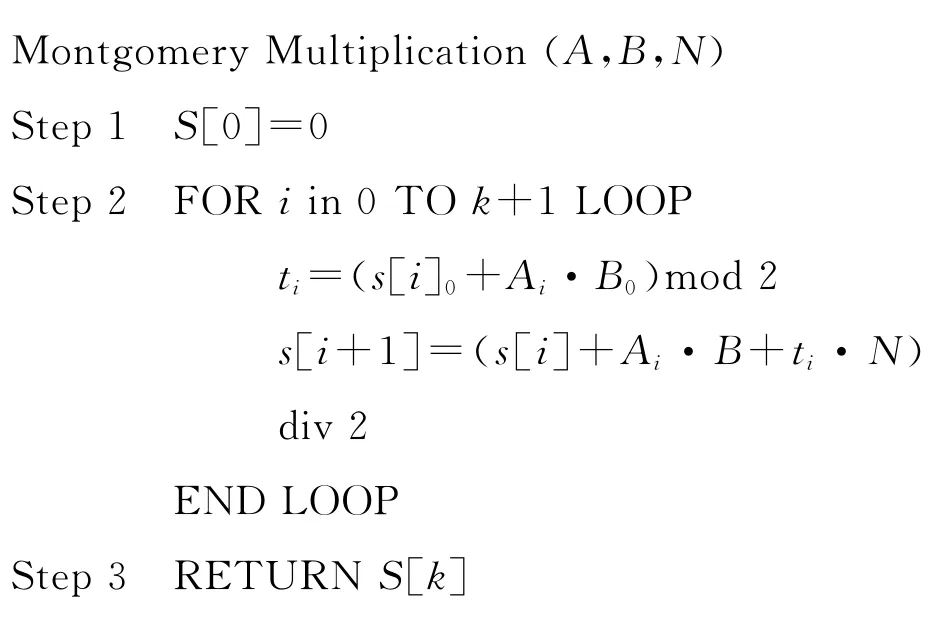
2.1 采用CSA的蒙哥马利算法
当位数很大时,算法2第2步中的加法运算会产生很大的延时,而采用CSA(Carry-Save-Adder)可以有效地避免长进位链所带来的延时[3].CSA 中FA 的逻辑如下:

CSA 由k个FA 构成,如图1所示.

图1 CSA 的结构Fig.1 The structure of CSA
因此采用CSA 的算法如下:
算法3


在算法3第3步中含有一个大数的加法,因此 文 献[4]使 用 了CPA(Carry-Propagation-Adder)利用多个时钟周期来完成最后的模乘输出.算法结构如图2所示.

图2 CSA-蒙哥马利算法结构Fig.2 The structure of CSA-Montgomery algorithm
2.2 本文对CSA-蒙哥马利算法的改进
从CSA-蒙哥马利算法中可以看出,每次循环中所加的数为0、B、N、B+N中的一个,因此将其中一个CSA 的结构进行改变,即CSA_ADD,如图3所示,并且利用其在第一个时钟周期计算出B+N,通过{SUM0,Ai}来判断CSA 的下一个输入值,循环最后(SUM+CARRY)的值可以再次利用CSA_ADD 来计算,舍去了CPA 的使用,不但提高了速度,而且减少了资源使用.改进后的算法结构如图4所示.
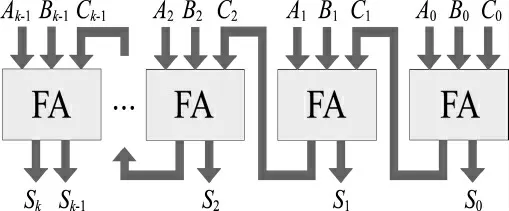
图3 CSA_ADD 的结构Fig.3 The structure of CSA_ADD

图4 改进后的CSA-蒙哥马利算法结构Fig.4 The structure of modified CSA-Montgomery algorithm
改进后的算法如下:
算法4

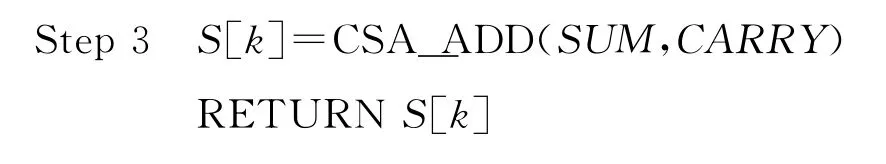
3 RSA 的算法实现
本文采用从右到左的方式扫描二进制的指数E,由于蒙哥马利算法的返回值是A·B·2-(k+2)modN,为了得到A·BmodN,必须先进行一步预处理Z=M_M(M,R,N),P=M_M(1,R,N),其中R是与N相关的常数,R=22(k+2)modN,最后再进行一次后处理P=M_M(1,P,N),即得到P=MEmodN,其中M表示明文,E表示指数,N表示模数.具体步骤如下:

4 性能分析
本文利用Verilog 实现了密钥位数可调的RSA 加解密处理器,利用Modelsim 仿真工具对RSA 核进行了仿真,并在XILINX 的VIRTEX5上得到了验证.如图5所示,当P=MEmodN=69mod 11=2,与仿真结果一致.

图5 RSA 核的仿真Fig.5 The simulation of RSA core
当加密处理器配置为1 024 位时,一次蒙哥马利模乘运算需要1+1 026+1=1 028个时钟周期.如果指数E的0、1 出现次数相当,则一次RSA 加解密需要大约1 024+500+3=1 527次模乘运算,最差情况需要1 024×2+3=2 051次模乘运算,则最差需要2.1×106个时钟周期,相比文献[5]减少了2.84%.当时钟周期为120 MHz时,1s内可以进行约75次加解密运算.密钥长度为1 024bits时的性能参数如表1所示.

表1 密钥长度为1 024bits的加密处理器性能参数Tab.1 The performance of cryptoprocessor with 1 024bits key length
5 结 语
本文对采用CSA 的蒙哥马利模乘算法结构进行了改进,省去了CPA 的使用,不但节省了器件资源,而且提高了算法速度.同时,利用Verilog编写了可配置密钥长度的RSA 算法的IP 核,应对不同工程的需要,可以灵活地改变密钥长度.
[1] Manochehri K.Modified radix-2 Montgomery modular multiplication to make it faster and simpler[C]//Proceedings of the International Conference on Information Technology:Coding and Computing(ITCC′05).Piscataway:IEEE Computer Society,2005:598-602.
[2] Blum T.Montgomery modular exponentiation on reconfigurable hardware[C]//Proceedings of 14th IEEE Symposium on Computer Arithmetic.Piscataway:IEEE Computer Society,1999:70-77.
[3] McIvor C,McLoone M,McCaany J V.Fast Montgomery modular multiplication and RSA cryptographic processor architectures [C] //Conference Record of the Thirty.Seventh Asilomar Conference on Signals,Systems and Computers.Piscataway:IEEE,2003:379-384.
[4] 王 旭,董 威,戎蒙恬.基于改进Montgomery模乘算法的RSA 加密处理器的实现[J].上海交通大学学报,2004,38(2):240-243.WANG Xu,DONG Wei,RONG Meng-tian.Implementation of RSA cryptoprocessor based on modified Montgomery modular multiplication algorithm [J].Journal of Shanghai Jiaotong University,2004,38(2):240-243.
[5] Kwon Tack-won,You Chang-seck,Heo Won-seok,etal.Two implementation methods of a 1024-bit RSA cryptoprocessor based on modified Montgomery algorithm [C]//IEEE International Symposium on Circuits and Systems-ISCAS.Piscataway:IEEE,2001:650-653.
