基于分形理论的产品自组织配置设计过程规划方法
何 彬
(湖北理工学院机电工程学院,湖北黄石435003)
产品自组织配置设计是通过配置单元由低到高的组合形成满足客户个性化需求产品的设计过程,配置单元是产品自组织配置设计过程中的组合和决策主体,是结构化的知识单元[1]。
产品自组织配置设计具有分形特性。分形主要是指几何与形状具有局部和整体之间的自相似性[2]。随着该领域研究的深入,这种几何与形状的自相似性逐渐拓展到了结构与信息的自相似性上[3-7]。
配置单元的组合是产品自组织配置设计的主要过程,组合过程的分形特性主要体现在结构与信息上。首先,配置单元由低到高组合时,信息的演化具有分形特性[8];其次,具有组合特性的产品,组成其零部件的结构特征大多相似,可重构性较强,且数量受到一定范围的限制。因此,配置单元的组合过程可以用局部或整体的分形结构来表示,说明产品自组织配置设计也具有结构分形特性。
1 产品自组织配置设计中的分形测度模型
在产品自组织配置设计中,配置单元组合模型具有分形树结构,组合模型的分形树结构如图1所示。其中,图1A 为基准模型,图1B为分形树模型。图1 中的线段表示组合过程和方向,线段的端点或不同线段的交点表示组合过程的配置单元,数字代表配置单元的层次,标注为1 的节点代表最底层的配置单元。
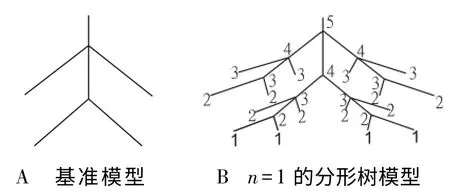
图1 组合模型的分形树结构
为了描述分形结构模型的规则程度和相关性质,采用如下几个参数进行测度。
1)分形维。
对于产品自组织配置设计中的分形树结构,可采用相似维数[6],在传统的非欧氏几何的分形理论中,相似维数主要用于度量几何结构或图形的不规则程度。一般来说,如果一个结构或图形有aD个相似单元,且相似单元与原图形存在1/a的几何比例关系,则指数D 具有维数的性质,此维数即为相似维数。
如果描述产品自组织配置设计过程的组合模型可用分形树结构表示,则局部与整体或阶段与全局就具有自相似性,但不能简单地用比例缩放关系予以刻画,须根据分形树结构的特点进行描述。
在配置单元组合过程中,具有分形树结构的组合模型,其分形维Dsc用类似于相似维数的测度方法,即:

其中b 表示如图1 基准模型中叶节点处配置单元的数量,叶节点是指不经过组合的配置单元。图1基准模型中b 值为4,a 表示如图1 基准模型中根结点到相邻层的分解次数,图1 基准模型中a 值为3。因此,根据公式(1),图1 中递归深度为2 的结构分形维数为1.262。可以看出,如果基准模型只有一级分解,其Dsc恒等于1,对于多级分解的情况,Dsc通常是大于1 的非整数,Dsc的大小从一定程度上反映了配置单元组合过程的复杂性。
2)递归深度。
递归深度体现了配置单元从低到高组合过程中递进的次数,用z 表示。在组合对象相同的情况下,递归深度越大,形成的组合方案就可能越少,对于具有完整分形的组合模型,如果给定基准模型的结构、z 和Dsc,则可计算出处在叶节点位置的配置单元数量,从而得到最终组合方案的结构特征数量。因此,如图1所示具有完整分形的组合模型,其叶节点的数量可按照公式(2)计算,即:

因此当递归深度z 为2 时,图1B 中叶节点的数量为16。
3)配置单元的层次和分解级数。
在分形树结构中,配置单元的层次反映了该配置单元所在的节点到根结点的节点间隔数,最高层次即为组合模型的总层次,为最底层节点到根结点的节点间隔数加2,总层次n 和递归深度z可表示为:

De 为基准模型中根结点分解的级数,不同于式(1)中的a,图1 中,基准模型根结点De=2,a=3,当递归深度z=2 时,最底层配置单元节点1 距离根部节点5 的节点间隔数为4,组合模型的总层次为5,各节点所处层次如图1B所示。
基准模型、Dsc和z 决定了参与组合的配置单元数量、不同阶段层次的差异性和过程的结构模式,基准模型、分形维数Dsc、递归深度以及配置单元的层次和分解级数又综合反映了配置单元组合过程的复杂程度,过程越复杂,产品自组织配置设计的效率就会受到限制,因此合理划分配置单元组合过程,设计具有分形结构的组合模型,可以科学地规划产品自组织配置设计过程,从而实现有效和高效的配置。
2 产品自组织配置设计的分形规划方法
产品自组织配置设计的分形规划是对配置单元组合过程的合理组织和设计,是运用分形理论和方法,在已知不同层次配置单元及其构成关系的条件下,规划配置单元组合的模式和模型,从而在保证获取足量组合方案的前提下,尽可能减少产品自组织配置设计过程的计算量,提高设计过程的有效性和效率。
1)组合方案数量的计算。
已知处在第1 层、第j 层的配置单元分别为CU11和CUj,二者具有组成结构上的包含关系,如果用F 表示结构特征集,满足F11⊂Fj,并且Fj中有K 个与F11级别相同的结构特征,K≥2 则称CU11和CUj具有构成关系,可以运用分形树的方法规划从配置单元CU11到CUj的组合结构。
一级组合时的结构与组合方案数量如图2所示。如果CUi通过一个层次的组合直接形成CUj,则CU11形成CUj,在该层共需经过K-1 次组合可以得到,在CUi的组合过程中,形成组合方案的数量为:
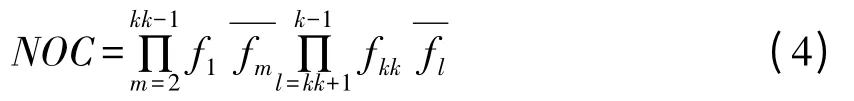
fkk、f1—分别表示CU11双向组合开始时备选的待配置单元数量;
kk—表示沿右向组合的次数,且K>kk>3。
根据式(4)可以推断,一层组合模式形成CUj时,组合方案数量最多,计算量也最大。因此,当K≥3 时,可运用分形理论,对从CU11到CUj的组合采用多级分形树结构,以避免组合方案过多造成计算量太大,如采取分解级数大于1 的基准模型。

图2 一级组合时的结构与组合方案数量
多级分形树结构的组合模型如图3所示。
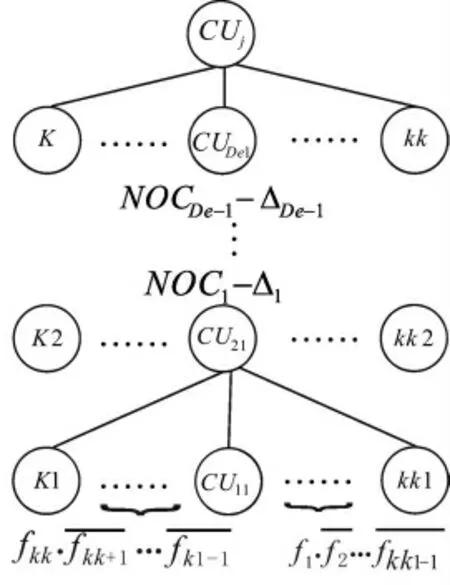
图3 多级分形树结构的组合模型
设基准模型的分解级数为De(De 为大于1的整数),根据产品自组织配置设计理论,每一级组合中一部分自相似度不能达到阈值要求的组合方案将被筛选;因此采用大于1 的分解级数时,最终的组合方案将显著减少,计算量也会相应减少。如图3所示,相邻层次配置单元CU11到CU21的组合方案数量为:

设一次组合后筛选掉的组合方案数为△1,则在NOC1-△1个可能形成CU21的方案上启动进行新的组合。因此,从CU21到CU31的组合方案数量为:形成CUj的最终方案数量为:

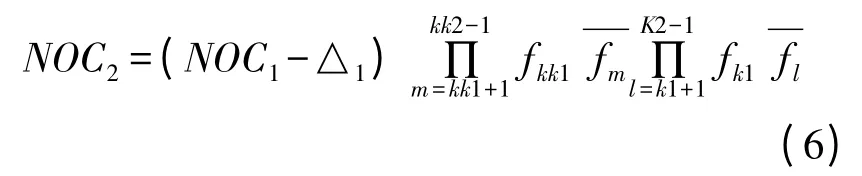
可见,分解级数De 越大,组合方案将越少,计算量也会相应减少,但是组合方案过少,优化的余地就越小,最终降低了配置的柔性和有效性,因此组合模型须合理规划。
2)单一配置单元之间组合模型的规划。
从CU11到CUj的组合是属于独立配置单元形成更高一级配置单元的过程。因此,K 和NOC 决定了模型结构,可按照如下原则进行规划。
①当K≤3 时,按类似于图2 的方式直接组合,此时分形维数为1。
②当K=4 或5 时,如果NOC 在允许值内,同样可直接组合;否则,分别按照图3 从CU11到CUj的组合模式进行组合。
③当K>5 时,可设最底层节点数为E,每一层分解的次数a 都相等,以及分解的节点数m=1,则有如下关系:

为避免组合结构过于复杂,减少组合过程的不确定因素,设定E∈{2,3,4,5},a∈{3,4,5}。可先按照式(5)中NOC1的值确定E,如果NOC1的值相对较大,并且E 取4 或5 时,且De<2,则更改E 的取值为2 或3,否则E 仍取4 或5;其次,根据NOC 与NOC1的比值估算a 的大小,若前者较大,则a 取较小值;否则,a 取较大值,从而通过De 来调整组合方案的数量。
3)2 个配置单元到一个配置单元之间组合模型的规划。
如果处在较低层次的2 个配置单元CU11、CU12组合为较高层次配置单元CUj,且满足F11⊂Fj,F12⊂Fj,F11和F12为同一结构特征级,Fj包含F11或F12级结构特征的数量为K,那么对于从CU11、CU12到CUj的组合模型规划,属于同时启动2 个配置单元组合为另一个配置单元的情形,规划过程如下:
①当K=2 或3 时,分别按照分解级数为1 时的标准基准模型规划从CU11、CU12到配置单元CUj的组合。
②当K=4 时,3 种典型的结构组合模型如图4所示。其中,图4b 为递归深度z=2 时的情形;图4c 与图1 基准模型相同,如果希望减少组合方案数量,选择组合结构b 或c,否则选a。

图4 K=4 时3 种结构组合模型
③当K=5 时,3 种结构组合模型如图5所示,结构的描述和选取类似于K=4 时的情形。

图5 K=5 时3 种结构组合模型
④当K>5 时,可先将CUj分解为较低级别的配置单元CU(j-1)1和CU(j-1)2,使得F11⊂F(j-1)1,F12⊂F(j-1)2,设K1和K2分别为F(j-1)1和F(j-1)2中的特征数,且满足K1+K2=K,然后参照单一配置单元组合为另一个配置单元的方法,分别规划从CU11到CU(j-1)1、从CU12到CU(j-1)2的组合模型。
3 实例应用
以某中型货车前悬架钢板弹簧的自组织配置设计过程为例,其设计需求:钢板弹簧总重量小于80 kg,疲劳寿命7 万次左右,价格中档,交货周期短。整车参数参照文献[8],其中偏频1.6~1.8 Hz,满载载荷1 617 kg,中心螺栓中心距UL=80 mm,轴距BL=3 500 mm,卷耳为两端上卷,一端包耳。按照分形规划的方法建立过程模型,根据过程模型由低到高组合。按照分形树模型和分形规划的方法,最终组合方案数量为2,便于比较和择优,而且整个过程实现起来快捷容易,充分体现了产品自组织配置设计的特点。
4 结束语
本文针对配置单元组合过程,运用分形树理论和方法,构建了产品自组织配置设计中的分形测度模型,并提出了配置单元组合过程的分形规划方法,并以汽车钢板弹簧自组织配置设计的实例验证了模型和方法的有效性。
[1]何彬.汽车钢板弹簧自组织配置设计的过程模型[J].黄石理工学院学报,2011,27(2):1-5.
[2]M E Sosa,S D Eppinger,C M Rowles.The misalignment of product architecture and Hubei Polytechnic University organizational structure in complex product development[J].Management Science,2004,50(12):1674-1689.
[3]K Ryu and M Jung.Goal-orientation mechanism in a fractal manufacturing system[C].International Journal of Production Research,2004:2207-2225.
[4]K Ryu,Y Son,M Jung.Modeling and specifications of dynamic agents in fractal manufacturing systems[J].Computers in Industry,2003,52(2):161-182.
[5]K Ryu and M Jung.Agent-based fractal architecture and modeling for developing distributed manufacturing systems[C].International Journal of Production Research,2003:4233-4255.
[6]S M Saad,A M Lassila.Layout design in fractal organization[J].International Journal of Production Research,2004,42(17):3529-3550.
[7]武志峰.基于分形理论的植物模拟方法研究[D].大连:大连理工大学,2005:38-40.
[8]何彬.汽车钢板弹簧自组织配置设计方法的研究[D].武汉:武汉理工大学,2009:64-65.

