超精密机床弹性微进给装置设计方法研究

张国智

(新乡学院机电工程学院，河南新乡453000)

随着计算机技术的飞速发展，各种工程软件也得到广泛应用。一个项目的完成，往往需要借助多个软件或模块，形成完整的系统开发过程[1]。目前，通过计算机仿真技术，实现对新开发产品的高效的一体化设计，包括拓扑优化设计、参数化优化设计、可靠性分析，并有效地结合有限元法[2]等虚拟仿真技术[3]，可改变主要依靠经验根据安全系数的传统设计方法，避免造成结构材料的冗余或不足，减少资源浪费或强度不足发生断裂等故障的发生[4－5]，但在具体机械领域中研究与应用尚不系统深入。

弹性微进给装置是超精密机床的重要装置，直接影响到超精密机床加工精度及表面加工质量，弹性微进给装置具有工作稳定可靠、精度重复性好的特点[6]。该装置的优化、可靠设计，可进一步提高其工作性能及工作的可靠性，目前，关于这方面的研究尚不深入。作者结合有限元仿真方法、拓扑优化设计、参数优化设计、可靠性分析方法等现代设计方法，研究基于以上的超精密机床的弹性微进给装置的一体化设计方法，从而找到最佳的优化、可靠的设计方案。

1 基于仿真技术的弹性微进给装置设计方案

基于有限元仿真手段，结合拓扑优化设计、参数优化设计、可靠性分析等现代设计方法，对超精密机床的弹性微进给装置进行一体化设计，从而达到了装置的优化设计，并且有效地保证了该装置的工作性能。具体的设计方案如图1所示。

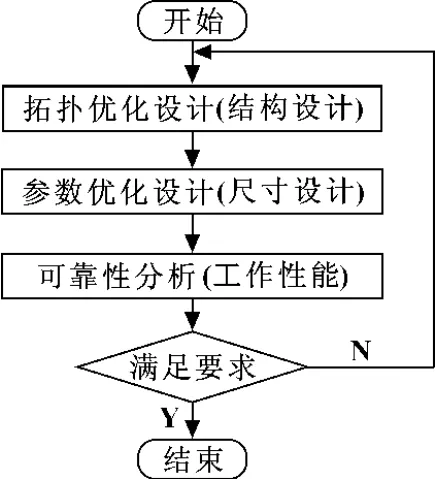
图1 弹性微进给装置仿真设计方案

2 弹性微进给装置基本结构及工作原理

弹性微进给装置是通过结构的弹性变形量来实现微进给的[6]，其结构原理如图2(a)所示，力学简图如图2(b)所示。

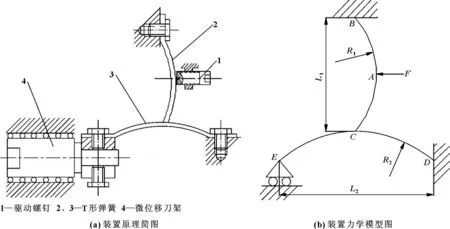
图2 弹性微进给装置原理简图

3 弹性微进给装置优化设计及可靠性分析

3.1 整体结构的拓扑优化设计

为了确定弹性微进给装置的设计结构，进行初步的拓扑优化分析，其拓扑优化的有限元模型如图3(a)所示，经过39次迭代，初步的拓扑优化结果如图3(b)所示。从计算结果可知:上部刚度对整体结构的刚度影响较大，下部刚度对整体结构的刚度影响较小。因而，在提高整体结构刚度的前提下，整体结构的上部刚度应设计大一些。

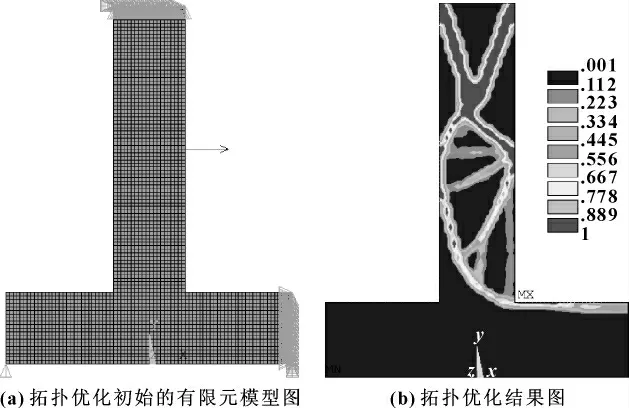
图3 拓扑优化的有限元模型及分析结果

3.2 整体结构的参数优化设计

在弹性微进给装置拓扑优化的基础上，对其进行具体结构的参数优化。在优化计算中，所用的参数及符号如表1所示，设计目标为装置的总体积，所选用的优化算法为子问题优化算法，最大迭代次数设为80次，在28次收敛，最后优化结果如表2所示，优化后最大应力为288.06 MPa，小于许用应力。

表1 优化设计参数 mm

表2 优化计算结果

基于图2(b)的力学模型，建立了其有限元模型，如图4(a)所示，施加的最大驱动力F=1 000 N，要求输出端E的位移在0.02～0.023 mm 内，优化后的有限元模型如图4(b)所示，迭代计算曲线图如图5所示，可见计算结果是收敛的。

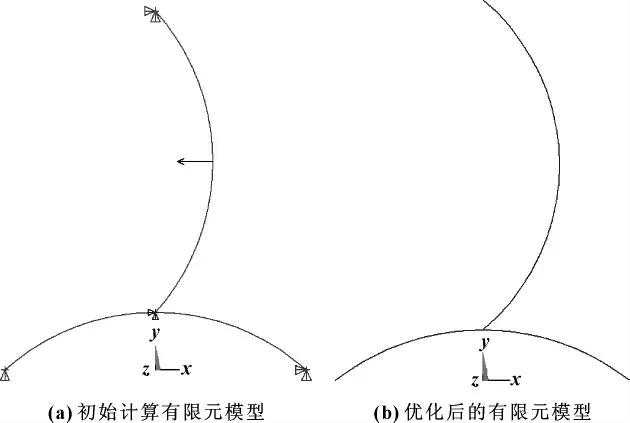
图4 初始计算有限元模型及优化后的有限元模型

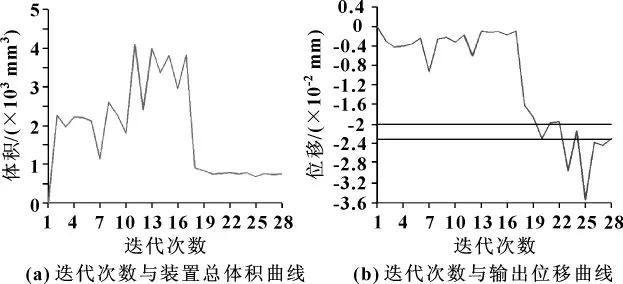
图5 迭代优化计算曲线

3.3 整体结构的可靠性分析

弹性微进给装置的有限元计算中的参数对应符号如表3所示，应用ANSYS的PDS 模块研究以上参数的随机波动性对装置输出位移的影响规律。采用蒙特卡罗法的直接拉丁抽样方法，迭代次数为10 000。

表3 微进给装置可靠性分析的参数

根据抽样计算结果，拟和出的响应曲面图如图6所示，可见:输出端位移随弹簧的长度L1和L2的增大而增大，但增加幅度不同。敏度分析结果如图7所示，可知:输出端位移对下部弹簧长度、上部弹簧长度最为敏感，而对泊松比最为不敏感。

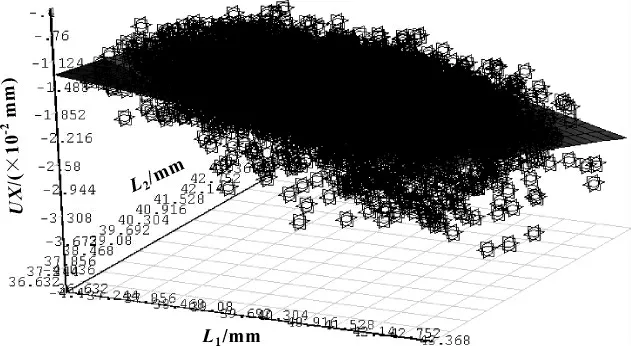
图6 抽样分析的响应曲面图

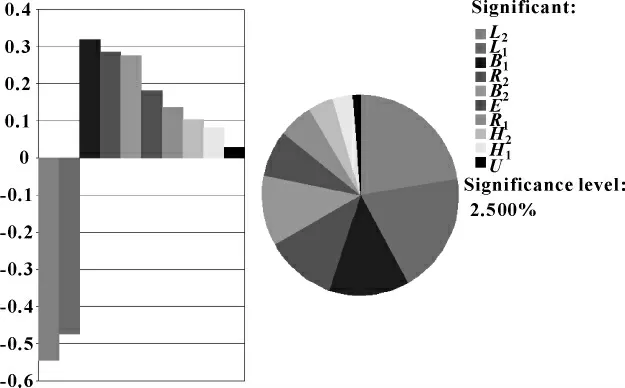
图7 敏度分析结果

10 000次的蒙特卡罗的计算结果如图8所示，累积分布函数计算结果如图9所示。

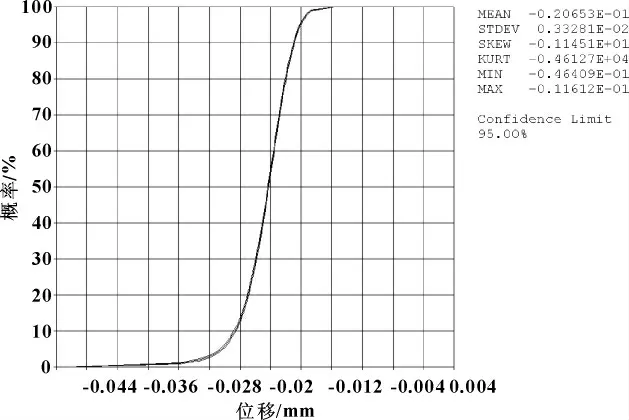
图9 累积分布函数图

从图8中可知，输出端的位移变化范围为0.012～0.042 mm。从图9中可知，输出端位移95%大于0.020 mm。从分析中可知:要保证装置的工作可靠性，应严格控制弹簧的设计参数及材料参数，尤其是弹簧的长度。

4 结论

针对超精密机床弹性微进给装置，首先提出了基于拓扑优化设计、参数优化设计、可靠性分析的一体化设计方法，建立了其有限元模型，并对该装置进行了拓扑优化设计和参数优化设计，找到了该装置的最佳设计方案;其次，基于概率有限元法中的蒙特卡罗法，研究了主要材料参数及所有的尺寸参数的随机性对该装置输出端的位移的影响规律。通过分析可知:该装置输出端的位移对下部弹簧长度、上部弹簧长度最敏感，而对泊松比最不敏感;并且，当各参数有5%正态随机波动时，输出端的位移变化范围为0.012～0.042 mm，要保证装置的工作可靠性，应严格控制弹簧的长度设计参数。文中的研究为超精密机床的弹性进给装置的设计及性能分析提供了新方法和工程设计依据。

【1】钱锋，张治.汽车零部件计算机模拟疲劳试验研究[J].学术论坛，2002(4):15－17.

【2】马建斌，李淑娟.基于ANSYS/LS-DYNA的奥氏体不锈钢切削模拟[J].机床与液压，2010，38(21):120－123.

【3】曾攀.有限元分析及应用[M].北京:清华大学出版社，2004:1－3.

【4】赵丽滨，张建宇，高晨光，等.基于结构可靠性的姿控/储能飞轮转子设计方法研究[J].宇航学报，2006，27(5):942－946.

【5】MOON Byung-Young，KANG Gyung-JU，KANG Beom-Soo.Dynamic and Reliability Analysis of Stochastic Structure System Using Probabilistic Finite Element Method[J].Structural Engineering and Mechanics，2004，18(1):125－135.

【6】张建华，盖玉先，刘军营，等.精密与特种加工技术[M].北京:机械工业出版社，2009.