点线矛盾检查中出现平三角形的处理方法研究

叶燕萍，董小军，叶骏

（1.浙江华东测绘有限公司，浙江杭州，310030；2.华东勘测设计研究院有限公司，浙江杭州，310014；3.浙江省隧道工程公司，浙江杭州，310013）

0 引言

点线矛盾也称为“高曲矛盾”，指高程注记点与周围等高线高程之间的相互矛盾［1］。造成点线矛盾的原因有多种，如人为因素、仪器稳定性、地貌特殊性、影像质量等［2］。点线矛盾的检查方法主要有目视检查法、邻近等高线法、等高线构TIN检测法［1］。人工检查是很费时费力的工作。因此，研究利用程序实现自动检查是非常有意义的。

等高线构TIN检测法检查精度高、检查结果可靠且运行速度快，是目前最常采用的方法。等高线构TIN检测法中，TIN的质量是一个非常重要的影响因素。从等高线生成TIN的方法有三种［3］：（1）将等高线离散化直接生成TIN方法；（2）将等高线作为特征线的方法；（3）自动增加特征点及优化TIN的方法。第一种方法不考虑等高线之间的约束关系，其模拟的地形会造成失真，使TIN中三角形的边穿越等高线，并且形成平三角形。第二种方法可以避免三角形的边穿越等高线的情况，但是也会形成平三角形。第三种方法通过增加特征点及优化TIN，可以消除TIN中平三角形现象。以该种方法为理论依据进行实验。

实验数据为Geodatabase格式的1∶2000 DLG，采用ArcGIS Engine组件构TIN。在研究其他学者对平三角形区域处理方法的基础上，提出了根据平三角形区域存在的非平三角形个数讨论平三角形区域的修复的算法，并用实验验证了等高线弯曲度比较大的地方及特殊地形（山顶或洼地、图幅边缘处、鞍部）平三角形区域处理方法的有效性。

1 TIN的建立

对数据进行过滤，仅留下等高线层，以等高线为约束边，采用ArcGIS Engine组件技术构TIN。利用各种约束条件构建的不规则三角网，由点、边、三角形构成。而组成三角形的边有三种类型：普通边（Regular edge）、硬边（Hard edge）、软边（Soft edge）。在构建三角网时，地理要素的约束条件为“Hard”类型。

2 平三角形区域地性线树的建立

2.1 产生平三角形的区域

平三角形是指三个顶点的高程值都相同的三角形。出现平三角形的原因是因为该区域缺少地形特征线信息，从地形地貌上来说，出现平三角形的区域也是地性线树存在的区域［4］。

平三角形存在的区域主要有［5］：（1）等高线弯曲度较大的地方：在一条等高线弯曲度较大的地方，同一个三角形的三个顶点可能来自于同一条等高线，从而形成平三角形；（2）山顶或洼地：山顶或洼地的闭合等高线内部，因为缺少相邻等高线，而在构TIN时不允许三角形穿越等高线，所以形成平三角形；（3）鞍部：有两个或两个以上的山顶或洼地形成鞍部区域，两条等值等高线参与构网，从而形成了平三角形；（4）图幅边缘处：靠近图幅边的单条等高线，由于缺少包含的等高线，无法实现相邻等高线的构网，从而形成平三角形。其中（1）有且仅有一个非平三角形；（3）有两个或两个以上的非平三角形；（2）、（4）没有非平三角形。

2.2 平三角形区域的搜索

平三角形的坡度为0，因此，采用坡度为0的条件可以查找出平三角形区域［6］。同时还需要把与平三角形区域相邻的非平三角形也搜索出来，加入平三角形区域。如图3，多边形ABCDEFGHIJ为平三角形区域，△PAJ为非平三角形，将它们合成一个整体考虑。点P称为高低点（高低点只会出现在含有非平三角形的平三角形区域内），平三角形区域的其他三角形顶点称为平点。若该平三角形区域没有非平三角形，则需要知道相邻等高线的高程值以便地性线树的建立。查找相邻等高线高程值的方法为：搜索与平三角形区域相邻的非平三角形，以该三角形非公共边上的那个顶点高程作为平三角形区域相邻等高线的高程值。

2.3 地性线树的建立方法

见图3，平三角形区域中当前三角形只有一个相邻三角形的称为一类三角形，如△PAJ；当前三角形有两个相邻三角形的称为二类三角形，如△JAB；当前三角形有三个相邻三角形的称为三类三角形，如△JBG。一类三角形主要出现在地性线树的端点，三类三角形出现在地性线的分支，其余的情况都是二类三角形。

图1 各类三角形的中轴线连接Fig.1 Connection of axes of various types of triangles

对平三角形区域建立地性线树时需考查每个平三角形与相邻三角形的关系，从而建立各类三角形的中轴线连线。一类三角形连接的是唯一公共边的中点与其相对的顶点，二类三角形连接的是两条公共边的中点，三类三角形连接的是三角形的重心和三条公共边的中点，见图1。地性线是相互连接在一起的树状分支结构，可以用二叉树来描述，见图2，A作为根结点，G、I、K、F为叶子结点，地性线树上的其他结点作为非叶子结点。

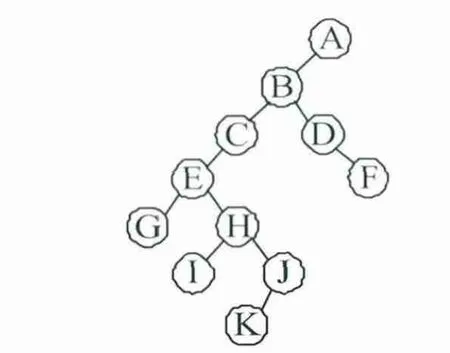
图2 地性线树的二叉树结构Fig.2 Binary tree structure of terrain structure line

地性线树的数据结构定义如下：

根据平三角形区域存在非平三角形的个数分三种情况讨论地性线树的建立，即（1）存在一个非平三角形，如等高线弯曲度较大处；（2）存在两个或两个以上的非平三角形，如鞍部；（3）没有非平三角形，如山顶、洼地、图幅边缘处。

2.3.1 等高线弯曲度较大处平三角形区域地性线树的提取

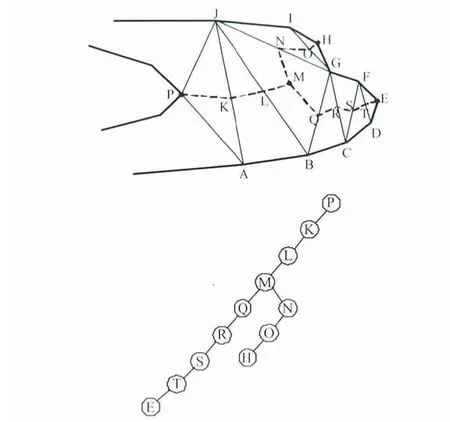
图3 等高线弯曲度较大处地性线树的提取Fig.3 Extraction of terrain structure line in the contour with large curvatures

等高线弯曲度较大处是平三角形可能存在的区域。该区域中存在一个非平三角形。以下是该区域平三角形处理的算法思想。

步骤1：先把高低点所在的非平三角形作为当前三角形，将高低点作为地性线树的根结点，根结点作为当前结点；

步骤2：然后将高低点所对边的中点作为左子结点，左子结点作为当前结点；

步骤3：根据当前结点所在的边搜索位于该边左边的三角形，并将该三角形作为当前三角形，搜索当前三角形另外两边相邻三角形的个数：

（1）若另外两边都有相邻三角形，则追踪当前三角形的重心，如果当前结点的左右子结点都为空，则将重心结点作为其左子结点；如果当前结点的左子结点不为空，则将重心结点作为其右子结点。然后把重心结点作为当前结点，取其中一条边的中点作为当前结点的左子结点，将左子结点的相关信息进行入栈操作；取另外一条边的中点作为当前结点的右子结点，右子结点作为当前结点，执行步骤3进行递归操作。

（2）若另外两边只有一条边有相邻三角形，则追踪到有相邻三角形边的中点，将该中点作为当前结点的左子结点，并把左子结点作为当前结点，执行步骤3进行递归操作。

（3）若另外两边都没有相邻三角形，则追踪到当前结点所在边相对的三角形顶点，说明已经追踪到地性线树的另一端，该顶点作为叶子结点；然后将栈顶信息出栈，根据出栈信息，继续追踪地性树的另一个分支。

2.3.2 鞍部平三角形域地性线树的提取

鞍部也是平三角形存在的区域，该区域存在两个或两个以上非平三角形，见图4。

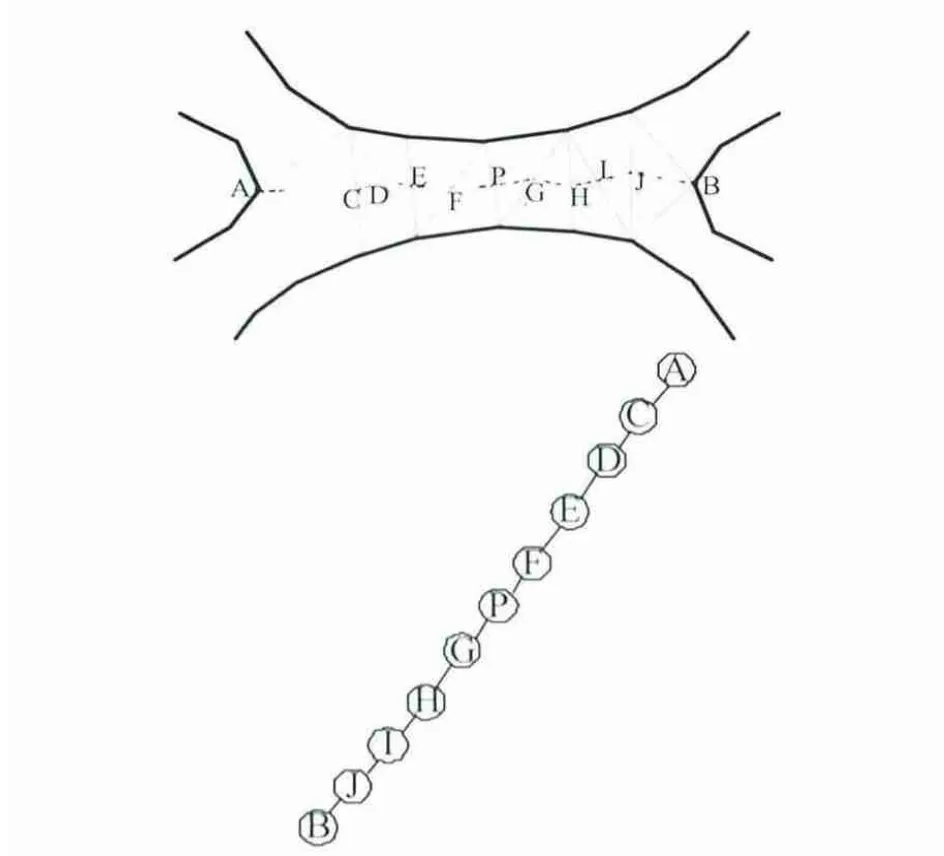
图4 鞍部地性线树的提取Fig.4 Extraction of terrain structure line in the saddles

在鞍部有两条或两条以上的等高线参加构网。对于有两个山头的鞍部，可能形成两种形态的平三角形区域，两者都是对鞍部真实地形的扭曲：第一种将鞍部削平成“低平原”，如图4（a）所示；第二种将鞍部填高成“高平原”，如图4（b）所示。两者的处理方法相同，都是利用提取地性线信息来恢复真实地形［3］。如图4所示，一个典型的鞍部构网形成的平三角形区域，其中APB为平三角形区域的中轴线，即地性线树的主线，P为中轴线的中间点，A、B两点的高程值相同，因此，需要给P点指定一个高程值。P点的高程值取鞍部父等高线和子等高线高程值的平均值，即高低点高程和平三角形区域高程的平均值。

2.3.3 山顶或洼地、图幅边缘处平三角形区域地性线树的提取

在山顶、洼地、图幅边缘处的平三角形区域中没有非平三角形。在山顶或洼地，如果没有地形特征点参与构TIN，则山顶或洼地处等高线在内部构网时会形成平三角形区域。出现山顶被削平，洼地被填高的不合理情况。同样，先得到中轴线APB，如图5所示，然后为中轴线上的各个结点赋高程值。此处不存在所谓的“高低点”，因此无法直接进行高程值的分配。为了恢复原来的地形，首先要获得相邻等高线高程值H1，将H1与平三角形区域的高程值H2进行比较，若H1-H2＞0，则该地为洼地，地性线树主线的中间点P高程值为H2-△H/2（△H为等高距）；若H1-H2＜0，则该地为山顶，地性线树主线的中间点P高程值为H2+△H/2，然后以中间点P为界，对地性线树主线中间点两端的分支根据长度大小分别进行线性内插［5］。

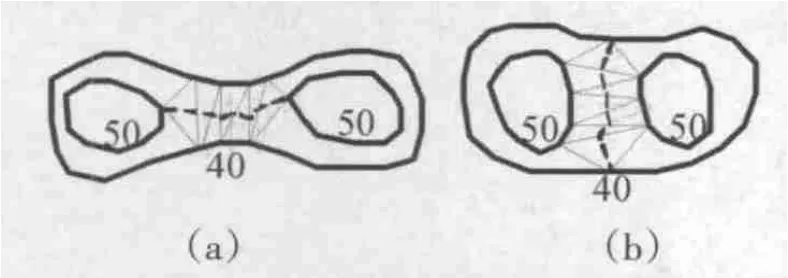
图5 鞍部平三角形区域存在的两种形态Fig.5 Two forms exist in flat triangular area of the saddle

图幅边缘处的等高线由于缺少相邻等高线，而在构TIN过程中三角形不可能穿越等高线，因此在等高线内部形成了平三角形区域。在这种情况下追踪地性线树的各叶子结点时，需要判断各叶子结点所在三角形边的情况，（1）若该三角形存在一条硬边，则叶子结点追踪到另一条非硬边的中点；（2）若该三角形存在两条硬边，则叶子结点追踪到两硬边之间的顶点；（3）若该三角形不存在硬边，则需要先追踪到该三角形的重心，然后再追踪到另外两条边的中点。追踪完地性线树后，得到地性线树的主线，这里不存在“高低点”，因此需要获得相邻等高线的高程值H1，把H1与平三角形区域的高程值H2进行比较：若H1-H2＞0，叶子结点为（1）、（3）两种情况，则叶子结点高程值为H2-△H/2（△H为等高距）；若H1-H2＜0，叶子结点为（1）、（3）两种情况，则叶子结点高程值为H2+△H/2。根据根结点与叶子结点的高程值，对地性线树主线上各结点以长度大小进行线性内插，由主及次，逐层计算，直到所有的结点都有高程为止。叶子结点为（2）的情况，该结点高程值为H2，这里计算各结点高程值参考山顶或洼地中的采用的方法。

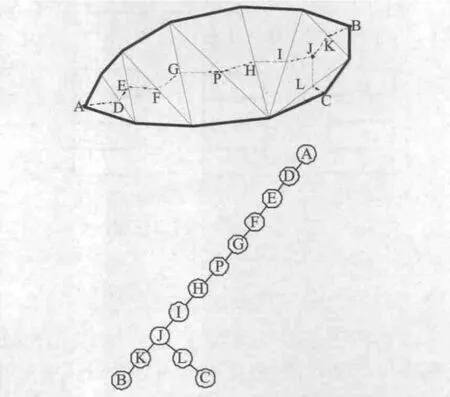
图6 山顶或洼地地性线树的提取Fig.6 Extraction of terrain structure line on the top of moun⁃tains or in the low-lying lands

2.3.4 追踪算法说明

在地性线树的追踪过程中，每追踪到一个结点，需要计算该结点到根结点的路径长度LenR，所取的值是该结点父结点的LenR值加上该结点到父结点的长度值。在所有的结点中，除了父结点和叶子结点有高程值之外，其余的结点赋高程初始值为-999，表示该结点没有实际高程值。

在本算法中采用了栈的数据结构，目的是为了在遇到地性线树分支过程中，保存分支结点的信息，以便在追踪完一个分支之后返回原来的结点继续追踪其分支。以图2为例，分支结点入栈出栈操作如图8所示。

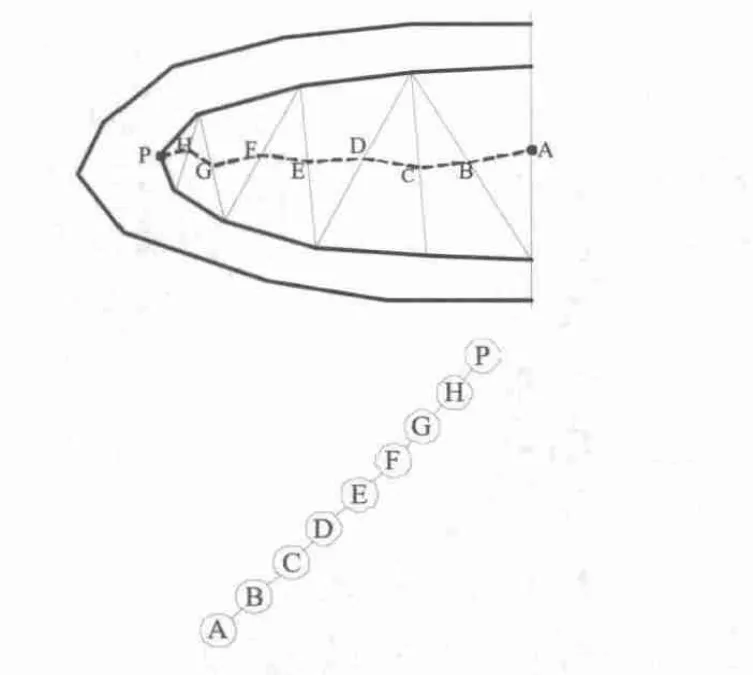
图7 图幅边缘处地性线树的提取Fig.7 Extraction of terrain structure line on the edge of maps

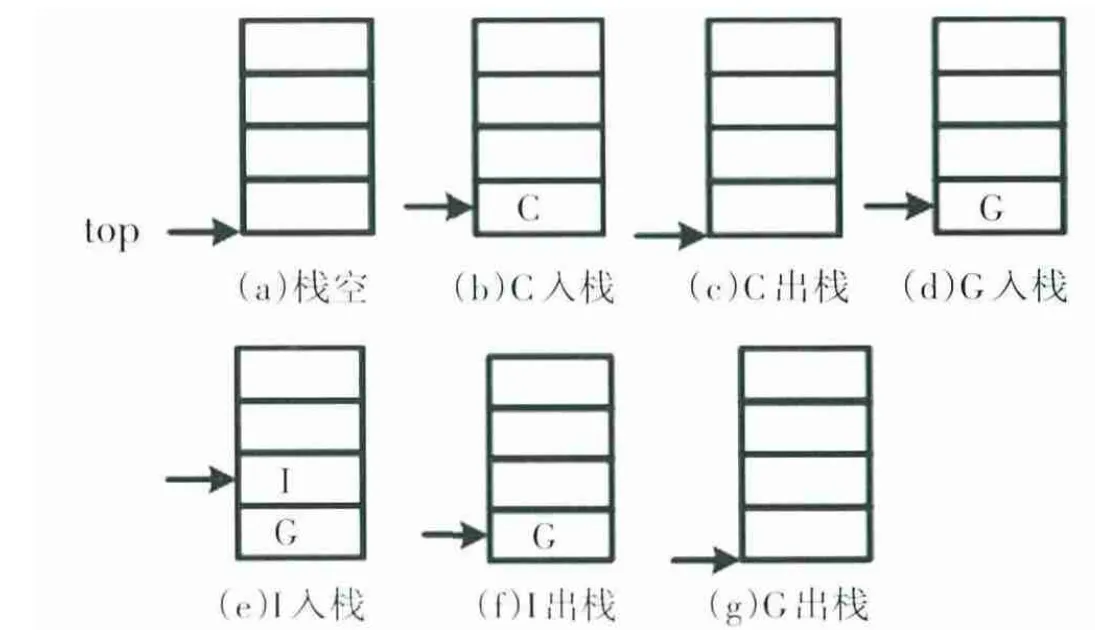
图8 分支结点入栈出栈图Fig.8 Branch nodes in and out of the stack diagram

2.3.5 地性线点高程计算

已知特征点的平面坐标，若要参加构TIN还需要内插出其高程值，地性线树的建立正是用来解决平三角形区域的高程分配问题［4］。提取出地性线树之后，从地性线树的根结点到各个叶子结点之间都存在一条路径LenRi（i=0…M，M为路径条数，即叶子结点的个数）。在所有的路径中，取LenR值最大的分支作为地性线树的主线，主线两端的根结点与叶子结点高程值是已知的，按长度大小对主线进行线性内插得到各个结点的高程。主线上所有的结点高程赋值完毕后，取出次长分支，根据分支根结点与叶子结点的高程值，对次长分支上的各结点以长度大小进行线性内插。

如图2为例，取地性线树的主线A-B-C-E-H-JK，已知根结点A和叶子结点K的高程值，根据长度为权进行高程分配，见公式（1）。

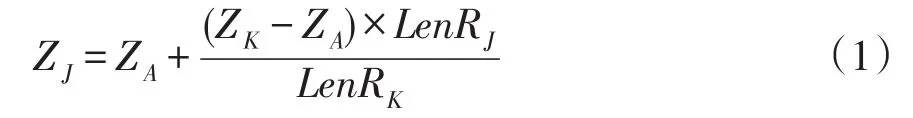
其中，ZJ、ZA、ZK分别为J、A、K结点的高程值，LenRJ、LenRK分别为J、K结点到根结点A的长度。依次类推，分别计算出主线上其余结点的高程值。取出次长分支B-D-F，已知分支根结点B和叶子结点F的高程值，根据长度为权计算出该分支的所有结点高程值。采用这种由主到次、逐层内插的方法直到地性线树上所有结点都有高程值为止。

将带有（X、Y、Z）值的地性线树结点信息放到平三角形区域中，以esriTinHardLine方式重新构网，得到一个合理的TIN。图9为消除平三角形前后的情况对比图。

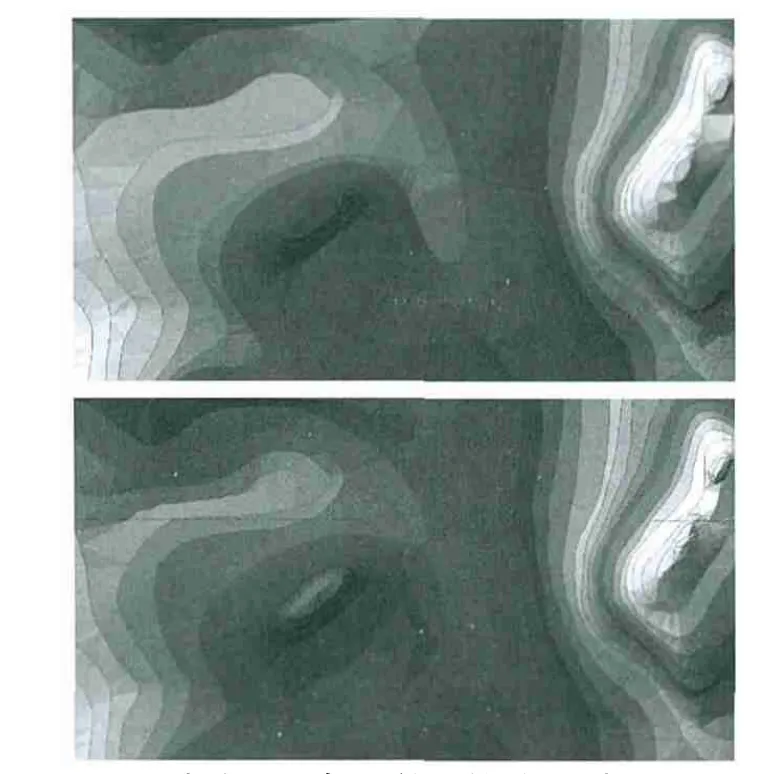
图9 消除平三角形前后的效果对比图Fig.9 Comparison before and after the elimination of flat triangle

3 点线矛盾的检查

点线矛盾检查中，根据每个高程注记点（X、Y）坐标，内插出其在TIN表面的高程，将内插出的高程值与高程注记点的属性高程值进行比较，若两者之差不在阈值内，则可能存在点线矛盾，将该高程注记点的相关信息记录到检查结果数据库中。

4 结语

经过实验验证，提取平三角形区域的地形特征线信息，并将该特征点信息加入平三角形区域重新构TIN，消除了在等高线弯曲度比较大的地方、鞍部、山顶或洼地、图幅边缘处的平三角形。在研究前人的基础上，对平三角形修复算法进行补充，提出根据平三角形区域存在非平三角形个数的方法对不同区域存在的平三角形进行修复。将平三角形修复方法引入点线矛盾质量检查，采用平三角形修复后的TIN进行点线矛盾质量检查，明显提高了点线矛盾质量检查的准确性。当然，这种方法只有在保证等高线质量的前提下才能使用，若等高线出现打折、相交、自相交等现象，该方法不适用。■

[1]何艳飞.1∶5万DLG质量检查系统及其关键问题的研究[D].成都:西南交通大学,2008.

[2]徐建达.航测地貌数据的质量控制[D].郑州:中国人民解放军信息工程大学,2002.

[3]李志林,朱庆.数字高程模型[M].武汉:武汉大学出版社,2003:6-52.

[4]陈仁喜,龙毅.顾及三角形处理的TIN建立算法[J].武汉大学学报,2003,28(5):619-622.

[5]吴永军,王燕午.基于ArcGIS Engine平三角形处理[C].中国地理信息产业发展论坛暨2008中国GIS协会年会论文集.

[6]于娟,张丽萍,张永忠.基于ArcGIS空间处理模型的TIN平坦三角形处理[J].地理与地理信息科学,2009(2)：113

[7]邸元.基于等高线建立DTM中平坦区域的一种处理方法[J].计算机辅助设计与图形学学报,2000,12(8):566-570.