基于CML的城市地铁网络相继故障分析＊

张海林 张铁岩

（交通运输部公路科学研究院国家智能交通系统工程技术研究中心1） 北京 100088）

（青岛市城市规划设计研究院2） 青岛 266071）

0 引 言

同自然界多数网络类似，城市地铁网络也是由线和点组成，是一种典型的复杂网络［1］．国内一些主要城市，如北京、上海、广州地铁建设已初具规模．随着网络规模的不断扩大，城市地铁也会出现一系列问题，例如，信号故障，乘客人数的骤增造成列车、站台过度拥堵等等．这些节点或边发生的故障会通过线路和车站之间的耦合关系扩散开来，从而引起其他节点故障，最终导致部分节点甚至整个网络的崩溃，这也就是通常所说的相继故障［2］．因此有必要对网络化条 件下城市地铁网络拓扑结构特性以及相继故障发生、发展进行研究，从而对故障的预防、控制提供理论依据．

国内对地铁网络相继故障已有初步研究．汪小帆等［3］在中对全局耦合网络、无标度网络及小世界网络中CML的相继故障进行了较为详细的阐述．Bao Zhejing，Cao Yijia［4］中对局域世界网络的CML的相继故障进行了研究．马秀娟［5］等提出有向网络CML的相继故障，并在文献［6］中对树形网络拓扑结构中的CML相继故障特征进行了探讨，马福祥［7］将 CML模型应用到km，n网络中，分析了km，n中不同网络拓扑结构的鲁棒性．以上研究主要集中在复杂网络拓扑结构类型方面，而对在地铁网络实例分析中则尚未涉及．本文采用基于耦合映像格子（CML）的相继故障模型和Matlab编程仿真，对北京、上海、广州等国内三个城市地铁网络相继故障进行了研究．

1 基本概念

1.1 耦合映像格子

多数时空系统的时间、空间和状态变量是连续的，适于用偏微分方程来描述．无论是进行理论分析还是数值计算，都比较复杂，而且运算量也大．耦合映象格子（coupled map lattice，CML）便是将时间和空间变量离散化，但状态变量仍保持连续，这样既克服上述缺点，又能从本质上显示出系统的复杂时空特性．它是一个时间、空间都离散，而状态保持连续的非线性动力学系统，已成为研究时空混沌的强有力工具．在过去几十年研究中，通常假设CML具有规则的拓扑结构（如全耦合或最近邻耦合）．近年来，随着复杂网络的兴起，人们已经开始研究具有小世界或无标度拓扑结构的耦合映像格子中的动力学行为，如时空混沌、分岔，同步等等［8］．

1.2 基于CML的相继故障模型

将具有N个节点的CML相继故障模型描述如下．

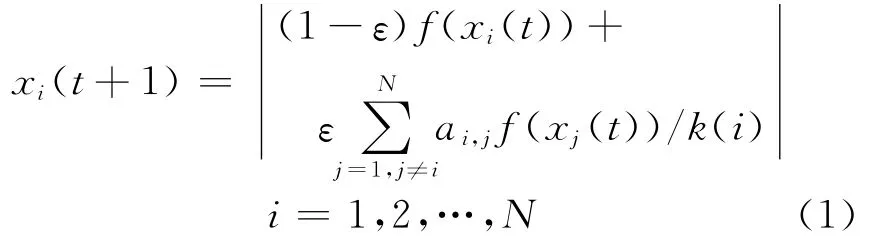
式中：xi（t）为第i个节点在t时刻的状态．N个节点的连接信息用邻接矩阵A ＝ （ai，j）N×N表示．若节点i和j之间有边相连，则aij＝aji＝1，否则aij＝aji＝0．这里规定任意2个不同的节点之间至多只能有1条边，且不允许节点和自身相连；k（i）是节点i的度；ε∈（0，1）为耦合强度；非线性函数f表征节点自身的动态行为，这里选择为混沌Logistic映射：f（x）＝4x（1－x），当0≤x≤1时，0≤f（x）≤1；式中的绝对值符号保证各节点的状态非负．

如果节点i的状态在m个时序内始终在（0，1）范围内，即0＜xi（t）＜1，t≤m，那么称节点i处于正常状态．如果在m时刻，节点i的状态xi（m）≥1，那么称节点在此刻发生故障，节点在以后的任意时刻状态恒等于零，即xj（t）≡0，t＞m．在节点状态按照公式（1）迭代演化的网络中，如果所有N个节点的初始状态都在（0，1）范围内，并且没有外部扰动，那么所有的节点将永远保持正常状态．

假设在m时刻给某个节点c施加一个外部扰动R≥1，如式（2）所示．

在这种情况下，节点c在第m 时刻发生故障．因此，对所有的t＞m 有xc（t）≡0．在第m＋1时刻，与c直接相邻的节点都将受到m时刻c节点的状态xc（m）的影响，并且这些节点的状态值按照式（1）计算得出．此时计算出来的节点状态值也有可能大于1，从而会引起新一轮的节点故障．这个过程反复进行，节点故障就可能扩散，最终导致网络的崩溃．

1.3 复杂网络特征参数简介

直径与平均路径长度：网络中2点之间的距离定义为连接2点的最短路径边数，其中任意两点之间距离的平均值称为网络的平均路径长度，记为L，任意两个节点之间的距离的最大值称为网络的直径，记为D；度是节点在复杂网络中的一个重要属性，是指与该节点连接的边数；聚类系数Ci又叫做群聚系数，定义为与该节点直接相邻的实际边数目与最多可能边数之比，整个网络的聚类系数＜C＞即为网络中所有节点聚类系数的平均值；节点介数是指网络中通过该节点的最短路径的数目．

2 相继故障仿真结果分析

对北京、广州、上海地铁网络构造说明如下，并统计得到3城市地铁网络特征值：（1）分析所用数据均来自各城市地铁运营公司官方网站，时间截止到2011年底；（2）地铁网络采用Space L构造方法，以地铁车站作为网络节点，若在实际网络中2站点之间有线路直接相连，则将其作为构造网络的1条边，并且在网络构造过程中对部分线路和站点进行了适当处理．对于部分孤立线路，比如北京地铁9号线、房山线和S2线，以及尚未开通站点均不在数据统计范围之内；（3）不考虑地铁线路方向和列车在线路上行驶时间，将地铁网络抽象为为无向非加权网络．对北京、广州、上海地铁网络拓扑结构特征值统计见表1．其中直径、平均路径长度、度、平均度在复杂网络中均为量纲一的量，在此指代不同情形下2点之间边的个数．

表1 各城市地铁网络拓扑结构特征值

本次仿真工具采用Matlab，图中数据均为50次实验的平均值，仿真过程中取ε＝0．6，并在第10个时刻选择攻击节点施加扰动R（R≥1）．实验采取两种攻击策略：随机攻击和蓄意攻击．其中在蓄意攻击时选取度较大的节点，对北京、广州、上海分别选取西直门、广州火车站、世纪大道作为攻击目标．首先读入网络邻接矩阵，求出相应参数，然后根据CML相继故障模型得到仿真结果，输出数据并画出关系图．

图1显示了城市地铁网络中在随机攻击和蓄意攻击两种策略下，扰动幅度R与故障规模I的关系曲线，从图中可以看出3座城市地铁网络的扰动幅度与故障规模均有相似的变化趋势，故障规模都会随着扰动幅度的增大而增加，并且在这两种攻击策略下均存在相似的阙值，．当R＜时故障规模I很小（I≤0．2），并且变化非常缓慢；当≤R≤时，故障规模I会迅速增加，并最终造成全局故障．从图中可以看到，该相继故障模型下，与随机攻击相比通过蓄意攻击引起相继故障进程稍有增加，但是效果并不明显．由文献［9］已知基于Space L的地铁网络的具有一定的随机网络特征，其度近似服从Poisson分布，多数节点度为2，度分布较为均匀，因此在相同的扰动幅度下，由蓄意攻击和随机攻击两种策略引起的相继故障规模不会有明显变化．

图1 单目标随机攻击和蓄意攻击条件下扰动幅度与故障规模关系

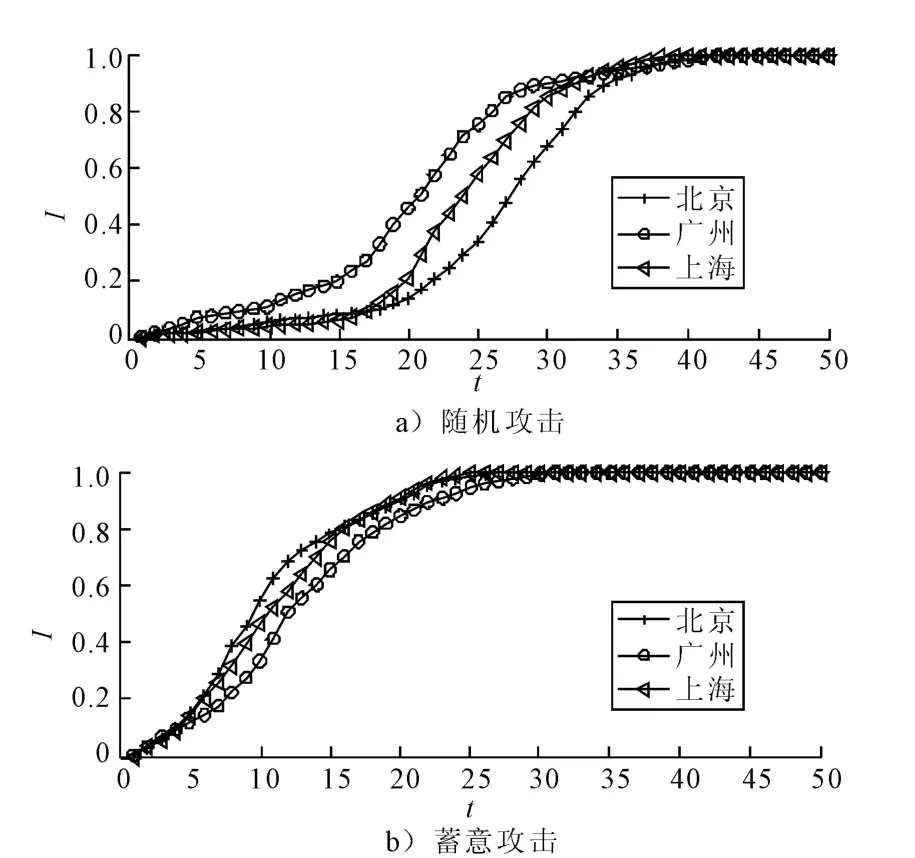
图2 相继故障在单目标随机攻击和蓄意攻击条件下的扩散过程

图3 多目标攻击下扰动幅度与故障规模关系

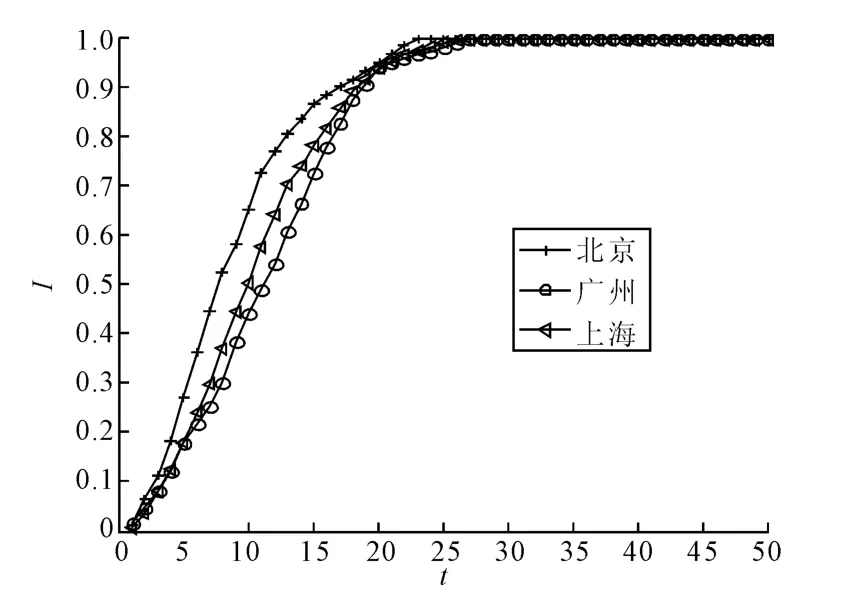
图4 多目标攻击下相继故障扩散过程

图2 是单个节点相继故障在地铁网络中的扩散过程，图2a），2b）分别表示了网络在随机攻击和蓄意攻击2种策略下故障规模的传播曲线，其中取扰动幅度R＝12．可以看到在同一攻击策略下地铁网络的相继故障扩散过程也呈现出相似的变化趋势．在第0时刻施加扰动后，蓄意攻击策略下在各个时刻引起的节点故障规模总是大于随机策略，并且故障规模一开始便有较快的增长速度，变化呈现出先快后慢的趋势；而随机攻击策略下网络故障规模呈现出“慢—快—慢”的变化趋势．同小世界网络相比，地铁网络在两种攻击策略下的相继故障传播均需要较长时间，这也验证了地铁网络具有较大的平均最短路径拓扑结构特征．

在进行多目标攻击时随机选取两个目标作为攻击对象，并施加扰动．同样取耦合强度ε＝0．6，图3为多目标攻击下故障规模随扰动幅度变化关系曲线，从图中可以看到同单目标攻击相比，故障规模没有明显变化，这是因为对于单目标攻击而言，当某个站点发生故障并向外传播时便出现和多目标攻击相似的情形，因此造成两类攻击除初始时刻之外并没有较大差别．图4为多目标攻击条件下相继故障规模随时间的变化情形，在这里同样取R＝12．可以看到在多目标随机攻击时故障规模的变化趋势明显快于单目标情况．同单目标随机攻击相比，在进行多目标攻击时3城市地铁网络达到全局故障的时间提前约40%．以上表明对于地铁网络多目标攻击只是加快了相继故障的传播速率，但对最终引起的网络故障规模并没有太大影响．

3 结束语

通过对北京、广州、上海地铁网络拓扑结构和相继故障分析得到以下结论：同许多其他网络类似，在进行单目标攻击时，地铁网络CML蓄意攻击下故障扩散过程比随机攻击要剧烈，具有较快的传播速度；但当相继故障经过充分传播时，通过蓄意攻击造成网络故障规模效果并不明显；同单目标攻击相比，地铁网络的多目标攻击只是加快了其相继故障的扩散进程，对于最终引起的故障规模则影响不大．

本文只是在城市地铁网络物理层面分析其相继故障，而未考虑运营交路、乘客换乘等诸多复杂情况，需要结合地铁网络实际情况做进一步研究．

［1］BARABASI A L．Linked：the new science of networks［M］．Massachusetts：Persus Publishing，2002．

2CRUCITTI PLATORA VMARCHIORI M．Model for cascadingfailures in complex networks［J］．Physica A，2007，386：407－413．

［3］汪小帆，李 翔，陈关荣．复杂网络理论及其应用［M］．北京：清华大学出版社，2006．

［4］BAO Zhejing，CAO Yijia．Cascading failures in localworld evolving networks （English）［J］．Zhejiang Univ，Sci．A，2008，9（10）：1336－1340．

［5］马秀娟，赵海兴，马福祥．基于耦合映像格子的有向网络相继故障［J］．计算机应用，2011，31（7）：1952－1955．

［6］马秀娟，马福祥．树形网络拓扑结构CML的相继故障［J］．青海师范大学学报：自然科学版，2010（3）：35－38．

［7］马福祥，马秀娟．基于CML模型的km，n网络拓扑结构相继故障分析［J］．济南大学学报：自然科学版，2010，24（2）：185－188．

［8］陈雍君，周磊山．基于时延耦合映象格子的相继拥堵模型［J］．电子与信息学报，2008，30（4）：988－990．

［9］汪 涛，方志耕，吴 卉，等．城市地铁网络的复杂性分析［J］．军事交通学院报，2008，10（3）：24－28．