车身疲劳载荷谱的位移反求法

方剑光，高云凯，徐成民

（同济大学 汽车学院，上海201804）

汽车在行驶过程中，由于路面的不平整，车身结构通常会受到交变载荷的作用，这种交变载荷经常引起车身疲劳强度失效.为了确保车身结构在规定的使用期内不发生疲劳破坏，在车身设计阶段必须对车身结构进行疲劳分析.

目前，计算机辅助工程（CAE）方法在汽车设计领域应用已经非常广泛，它能在设计阶段预测和解决车身可能存在的问题.同时，还可通过对不同方案模拟试验的比较，辅助确定一个较为合理的试验方案.高云凯等［1］用 Matlab生成路面激励载荷，结合整车多体动力学模型获取车身疲劳分析的激励载荷，采用瞬态时域法计算出车身的动应力，并利用MSC.Fatigue软件分析燃料电池大客车车身的疲劳寿命.孟瑾等［2］采用多体动力学和有限元法联合仿真，基于多轴疲劳理论预测某型轿车车身的疲劳寿命.赵婷婷等［3］综合应用多体动力学有限元法和疲劳分析方法，对某微型货车的车身进行疲劳分析与优化.Kim等［4］在客车车体的耐久性分析中提出一种计算车辆动载荷的仿真方法，且使用DADS软件进行刚柔体模型的混合建模和分析.

在疲劳寿命预测中，获得研究对象正确的边界载荷，是准确预测其疲劳寿命的先决条件.在上述文献中，多体动力学仿真都是以编制的路面位移载荷输入，车身接附点的载荷谱从多体动力学仿真中提取.一方面，由于不是真实的道路载荷谱，提取的车身载荷的准确性缺乏说服力；另一方面，多体模型中轮胎力学特性的模拟是国内外比较棘手的难题，需投入大量的时间和资源［5－7］.因此，在这种情况下不能贸然将多体动力学仿真中车身接附点的载荷用于车身疲劳计算.

本文以某商务车作为研究对象，基于试车场载荷谱采集和多体动力学仿真，运用轮心位移反求法获取车身载荷谱，旨在为车身疲劳寿命预测提供准确可靠的载荷输入.

1 车身载荷的轮心位移反求法

车身载荷的轮心位移反求法结合试验数据的采集和多体动力学仿真，是一种载荷求解的混合法或半解析法［8］.首先，测量必要的响应信号（包括目标信号和监控信号），它们是反映汽车底盘和车身耐久性的参数，包括轴头垂向加速度、车身地板加速度、车轮与车身间的相对位移等；然后，建立悬架系统的多体动力学模型，基于多体模型与试验载荷数据进行虚拟迭代，并获取车身载荷谱.轮心位移反求法的实现流程如图1所示.

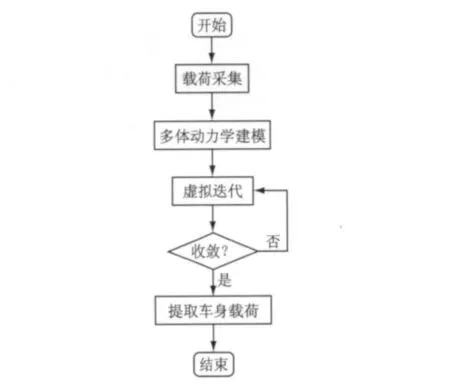
图1 轮心位移反求法流程图Fig.1 Flowchart of spindle displacement back－calculation

轮心位移反求法的特点是以轮心的位移载荷作为多体模型的驱动信号，这将避开复杂轮胎模型的建立.同时，与力载荷相比，位移载荷可以避免自由车身在多体动力学仿真中的不稳定现象，即不会导致车辆模型的漂移和翻转［9］.

2 信号采集

选择四个车轮轴心位置的六分力为后期迭代目标测量信号，并选择各轴头、减振器、螺旋弹簧等位置布置传感器作为监控信号，所用的数据采集传感器列于表1，具体传感器的布置如图2所示.信号采集在襄樊试车场各个典型路段进行，包括比利时路、大卵石路、共振路等.采集后的信号需经过必要的处理，其中前减振弹簧的应变信号经标定处理后转化为减振器上下端相对位移信号.

3 多体动力学建模

根据前期测试得到的底盘参数，包括悬架硬点坐标、满载簧载质量及其质心和转动惯量、悬架的避振弹簧刚度曲线、减振器阻尼曲线、橡胶衬套各向刚度信息等，用MSC.ADAMS软件建立该车的多体动力学模型，如图3所示.其中，前悬架为麦弗逊悬架，由减振器总成、摆臂、横向稳定杆以及转向系统组成，后悬架为非独立悬架，由钢板弹簧、减振器、限位块以及车桥组成.车身采用质量点建模，与悬架通过衬套连接.应指出的是，轮心位移将直接作为整车模型的驱动，故模型中不包含轮胎.

表1 数据采集传感器Tab.1 transducers for data acquisition

图2 传感器布置Fig.2 Arrangement of the transducers

图3 整车多体动力学模型Fig.3 Multi－body simulation model of the entire vehicle

多体动力学模型的精确与否将直接决定最终车身载荷谱求解的结果.因此，有必要对模型进行修正和校核.首先，进行静态校核，即校核整备状态下各轮轮荷以及悬架缓冲块间隙.然后，进行动态校核.通常多体动力学模型中的阻尼等参数存在较大的不确定性，造成模型的精度不够.动态校核是通过模型参数的调校使得在同样的载荷激励下，多体动力学模型与物理样车具有相同的响应.

4 虚拟迭代

虚拟迭代本质上是求解非线性系统的逆问题：在系统响应量已通过试验采集得到的前提下，求解系统的外部驱动载荷.外部驱动载荷可以是力或位移，系统响应可以是加速度、速度、位移或者柔性部件的应力和应变.与台架物理迭代类似，整个虚拟迭代的流程包括系统辨识和目标信号迭代两个阶段.

（1）对多体模型进行系统辨识

首先，生成合理的辨识信号，通常为带通白噪声信号；然后，用生成的辨识信号作为输入对模型进行仿真分析，获得目标参考信号位置处的系统响应；最后，根据模型输出和辨识信号获取系统的频率响应函数矩阵.频率响应函数通过H1法估计，即由以下公式计算得到：

式中：Gxy（jω）为输入和输出信号的互谱密度函数，Gxx（jω）为输入的自谱密度函数.值得注意的是，由式（1）估计的频率响应函数自功率谱Gxx（jω）不能为奇异矩阵，这就要保证辨识信号的不相关性.其次，与物理迭代相比，虚拟迭代的优势在于其输入信号可以选择更大更接近实际的幅值，而不会因此过载损坏部件.这样识别出的频率响应函数更能反映系统的实际工作特性，在随后经较少次数的迭代便可收敛.

（2）目标信号再现

由期望信号和频率响应函数矩阵反推驱动信号时，由于系统存在非线性，使模型目标信号的响应值和试验值有误差，需要迭代逐步修正驱动信号.具体过程如下：① 根据目标信号的试验值和系统模型得到迭代的初始输入信号；② 将初始输入信号作为输入信号对系统进行仿真分析；③ 得到系统输出和目标信号试验值的误差；④ 根据误差信号来迭代修正系统的输入信号，其修正原理如下所示：

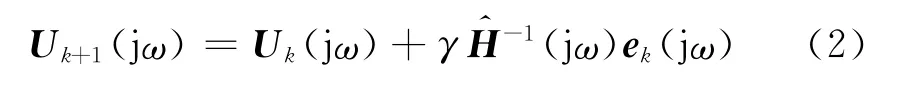
式中：Uk＋1（jω）为第（k＋1）次迭代的驱动信号，Uk（jω）为第k次迭代的驱动信号，γ为迭代步长，（jω）为辨识得到的系统模型，ek（jω）为第k次迭代的误差信号.

（3）收敛准则

通常，先将迭代过程中的目标信号和监控信号与相应的试验值进行时域和频域比较，判断整体趋势和幅值大小是否可以接受，目标信号要求更加苛刻，必须保证与试验值非常接近.

同时，由于最终得到的载荷用于疲劳寿命预测，还需从疲劳损伤角度评价迭代的收敛程度，通常结合给定的材料名义S－N曲线，采用相对损伤来评价，定义为

式中：μ为相对损伤，Diteration和Dtarget分别是迭代信号及其试验值的伪损伤.相对损伤越接近1.0，表明迭代的质量越高，一般认为迭代信号的相对损伤在0.5～2.0之间迭代比较成功［10］.

关于系统驱动信号的选择，力驱动会造成模型的漂移或翻转，因此本文提出的位移反求法将四个车轮的轴头垂向位移作为系统输入，而将垂向力作为目标输出信号，四个车身相对位移和四个车身加速度作为监控信号.

以比利时路为例，经过六次迭代达到收敛，迭代结果如图4，5和表2所示.目标信号（轴头力）的迭代值，无论是从时域、频域还是相对损伤角度都与试验值吻合度非常高；而监控信号的迭代值在时域和频域上与试验值具有一致的趋势和幅值，且相对损伤值也基本一致.同时目标信号（轴头力）的误差明显小于其他监控信号的迭代结果，这是由于目标信号的误差很大程度上取决于迭代的成败，而监控信号的误差则体现了仿真模型的建模精度.从迭代结果来看，多体动力学模型具有较高的精度，因此可基于此多体动力学模型提取车身载荷谱，用于后续的车身疲劳寿命预测.

图4 迭代结果（时域）Fig.4 Iteration results（in the time domain）

表2 迭代结果（相对损伤）Tab.2 Iteration results（relative damages）

图5 迭代结果（频域）Fig.5 Iteration results（in the frequency domain）

5 车身载荷谱分解

将最后一次迭代所得轴头垂向位移以及其余五个方向的力（或力矩）驱动多体模型便可得到车身疲劳寿命预测的载荷谱.车身与底盘共18个安装点，如表3所示，图6为前减振器安装点六个方向的力（或力矩）时间历程.

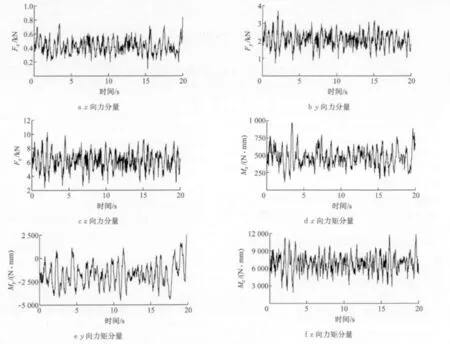
图6 左前减振器安装点载荷历程Fig.6 Load history on the interface point of the front left shock absorber

表3 车身与底盘安装点Tab.3 Body interfaces with chassis

6 结论

本文以某商务车为例，结合道路载荷谱试验采集与多体动力学仿真，详细论述了轮心位移反求法求取车身载荷谱的原理和流程.基于采集的道路载荷谱和多体模型进行虚拟迭代后仿真信号与试验值的一致性好，随后提取的车身载荷谱具有较高的可靠性，可用于车身疲劳寿命预测.

［1］ 高云凯，李翠，崔玲，等.燃料电池大客车车身疲劳寿命仿真分析［J］.汽车工程，2010，32（1）：7.GAO Yunkai，LI Cui，CUI Ling，et al.A simulation analysis on the fatigue life of fuel cell bus body［J］.Automotive Engineering，2010，32（1）：7.

［2］ 孟瑾，朱平，胡志刚.基于多体动力学和有限元法的车身结构疲劳寿命预测［J］.中国公路学报，2010，23（4）：113.MENG Jin，ZHU Ping，HU Zhigang.Fatigue life prediction of autobody structure based on multi－body dynamics and finite element method ［J］. China Journal of Highway and Transport，2010，23（4）：113.

［3］ 赵婷婷，李长波，王军杰，等.基于有限元法的某微型货车车身疲劳寿命分析［J］.汽车工程，2011，33（5）：428.ZHAO Tingting，LI Changbo，WANG Junjie，et al.Fatigue life analysis of a mini truck body based on FEM ［J］.Automotive Engineering，2011，33（5）：428.

［4］ Kim H S，Yim H J，Kim C B.Computational durability prediction of body structure in propotype vehicles［J］.International Journal of Automotive Technology，2000，23（1）：1292135.

［5］ Berzeri M，Dhir A，Ranganathan R，et al.A new tire model for road loads simulation：full vehicle validation［C］//SAE Paper.［S.l.］：SAE，2004：2004－01－1579.

［6］ Sui J，Hirshey J.Evaluation on Analytical Tire Models for Vehicle Vertical Vibration Simulation Using Virtual Tire Testing Method［C］.SAE Paper.［S.l.］：SAE，1999：1999－01－0786.

［7］ Haga H.Evaluation method for road load simulation using a tire model and an applied example［C］//SAE Paper.［S.l.］：SAE，2006：2006－01－1256.

［8］ da Cruz J，do Espírito Santo I，de Oliveira A.A semianalytical method to generate load cases for CAE durability using virtual vehicle prototypes［C］//SAE Paper.［S.l.］：SAE，2003：2003－01－3667

［9］ Bäcker M，Langthaler T，Olbrich M，et al.The hybrid road approach for durability loads prediction［C］//SAE Paper.［S.l.］：SAE，2005：2005－01－0628.

［10］ Ryu S.A study on obtaining excitation load of virtual test lab using virtual iteration method［C］//SAE Paper.［S.l.］：SAE，2010：2010－01－0011.