基于单站观测求取的位置差的特性分析

杨飞飞

(1.同济大学测绘与地理信息学院，上海 200092； 2.上海市测绘院，上海 200063)

基于单站观测求取的位置差的特性分析

杨飞飞1，2∗

(1.同济大学测绘与地理信息学院，上海 200092； 2.上海市测绘院，上海 200063)

GPS精密单点定位中，无模糊度模型，通过历元间差分技术来消除初始相位模糊度，求取历元间位置差，并通过位置与位置差的组合来完成精密单点定位。由于难以模型化误差改正、接收机噪声等误差影响，位置差参数中存在一定的误差。在进行位置差与位置结合过程中，当误差呈系统误差特性时，会对定位结果产生累积性作用。因此，对于误差特性的研究具有重要的意义。本文在求得位置差的基础上，研究了位置差误差的特性。

精密单点定位；位置差；误差

1 前 言

精密单点定位(Precise Point Positioning，PPP)是在1997年由JPL的Zumberge等人[1]提出并在他们开发的数据处理软件GIPSY上给予实现的，通过10年的发展，其在模型研究和应用方面都有了很大的发展。我国学者如武汉大学叶世榕博士[2]等也对精密单点定位技术进行了深入的研究。精密单点定位模型中，无模糊度模型通过历元间差分技术，消去初始相位模糊度来求取历元间的位置差，进而通过位置差与位置的组合来实现接收机轨迹的确定。由于难以模型化或者接收机噪声等的影响，求取的位置差参数中存在一定的误差。本文基于求取的位置差，研究了不同采样率位置差误差的特性及其统计性。

2 单站差分

历元间的差分通过化简可以写为[4～6]:

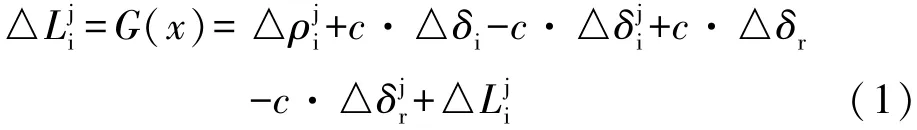
线性化并约简写为:

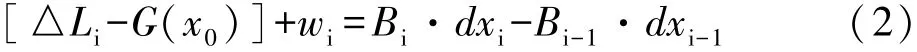
式中Bi，Bi-1分别为历元i以及历元i-1的系数矩阵，dxi，dxi-1为参数的改正数。

定义d△xi=dxi-dxi-1，li=△Li-G(x0)，式(2)可以重新写为:

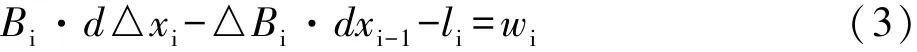
式中，△Bi=Bi-Bi-1，若忽略此项[4～6]，式(3)可以简化为:

由式(4)，得到法方程为:

当位置参数的初始坐标取真值时，就可以通过式(5)进行形变的监测。单站差分公式消除了模糊度参数的处理，大大简化了求解历元间位置差参数时的繁琐程序。

3 数据分析

通过作者研究，随着采样率的变化求解的位置差的精度会发生变化。当采样率增大时，位置差的解算精度会随之提高。虽然位置差精度随着采样率的增大，其精度有所提高，但由于解算过程中难以模型化误差改正、接收机噪声以及舍去误差等误差存在，位置差中总会有一定的误差存在，当误差呈系统误差时，会对定位结果产生累积性的影响。本文在不同采样率位置差结果基础上，通过小波分析理论进行误差特性的分析。其中1 s观测数据来源于2007年第299天在上海市测绘院采集的6 h的数据。1 s的小波分析结果(单位/cm)如图1～图3所示。

图1 X方向的位置差与去噪信号

图2 Y方向的位置差与去噪信号

图3 Z方向的位置差与去噪信号

历元间差分之后，剩余误差包括不能完全消除的卫星天线相位中心偏差、固体潮，小周跳及一些其他误差。从而使估计得到的历元间位置差具有一定的误差，这些误差在位置与位置差组合过程中会出现累积现象。对于静态观测来说，使得估计结果出现严重偏离X轴，由于静态观测时，历元间位置差近似为零。采用MATLAB中的小波分析工具箱，对1 s观测结果进行了分析。通过分析，发现图1波谷地方，图2，图3中的波峰地方有小周跳存在。

0.1 s观测数据来源于2007年第314天在上海市测绘院采集的观测数据。对0.1 s观测的解算结果进行了小波分析以及去噪操作。对应结果(单位/mm)如图4～图6所示。

从图4～图6中的去噪结果可以明显地看出，历元间位置差结果存在一定的系统偏差，在一定的时间里面，这一误差比较稳定。对于0.1 s观测来说，通过历元间差分可以完全消除掉卫星天线相位中心偏差、固体潮等。由此可以推断出，这一偏差产生的主要原因为小周跳的存在。小周跳的存在改变了历元间差分式(5)中的常数项，从而使去噪之后的结果在一定的地方出现突然地断裂。如图4～图6中的5 000、35 000历元附近有明显的凸起和跳跃。通过本文高频观测数据对应的历元间位置差的结果及其分析可以得到，在能完全地探测到小周跳之后，采用高频观测信号和本文提出的相关算法可以进行形变及其特性的研究。

图4 X方向位置差与去噪信号

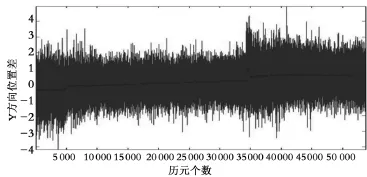
图5 Y方向位置差与去噪信号

图6 Z方向位置差与去噪信号

4 结 论

本文详细推导了历元间差分公式。通过具体实验，论证了单站差分的意义。通过不同采样率观测对应位置差结果的特性，可以得到，高频采样观测数据可以探测出较为细致的信号特性。通过对具体实验、结果的分析可以得到，一些难以探测的小周跳会对历元间位置差产生一定的影响。这样可以推断，如果能对GPS观测中的一些小周跳进行修复和探测，高频观测结果的去噪信号可以用来进行微小形变的监测。这也使得近年来采用高频GPS观测进行信号的提取，然后进行地震、形变的研究成为热点。

[1] Zumberge JF.Precise point positioning for the efficient and robust analysis of GPS data from large network[J].J.Res，1997.102：5005～5017.

[2] 叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉：武汉大学，2002.

[3] Hu Congwei，Chen Wu，Gao Shan，etc.Data Processing ForGPSPrecise Point positioning[J].Transact ions of Nanjing University of Aeronautics＆Astronautics，2005，22(2)：124～131.

[4] 韩保民，杨元喜.基于GPS精密单点定位的低轨卫星几何法定轨[J].西南交通大学学报，2007，42(1)：75～79.

[5] 陈俊平，王解先.基于历元间差分的低轨卫星运动学精密定轨[J].大地测量与地球动力学，2007，27(4)：57～61.

[6] 郑作亚，卢秀山.基于加权的伪距和历元闻相位差分模型GPS单点定位方法[J].测绘科学，2007，32(5)：47～49.

[7] 吴连大，贾沛璋.人卫光学观测中大异常值的剔除方法[J].天文学报，1994，35(2)：113～119.

[8] 吴江飞，黄城.抗差估计在星载GPS卫星非差运动学定轨中的应用[J].天文学报，2006，47(3)：320～326.

[9] Yang Y.Robust Estimation of Systematic Errors of Satellite Laser Range[J].Journal of Geodesy，1999，73：245～349.

[10] Yang Y.Robust Estimation of Geodetic Datum Transformation[J].Journal of Geodesy，1999，73：268～2641.

Analysis of the Position-Difference Based on the Observation of Single Receiver

Yang Feifei1，2
(1.College of Surveying and Geo-Information，Tongji University，Shanghai 200092，China；2.Shanghai Institute of Surveying and Mapping，Shanghai 200063，China)

In precise point positioning，the ambiguity can be canceled by using the epoch-differenced approach，when the free-ambiguitymodel is used.The position-difference can be estimated in thismethod.After estimation of the position-difference，the precise positioning is realized based on the initial coordinate component and position-difference. Because the estimated position-difference affected by the un-modeled error and other errors，its accuracy is not high.In positioning，the position resultswill affect by the cumulative characterization of the system error.In this contribution，the characterization of the epoch-difference is studied based on the estimated epoch-difference in this paper.

precise point positioning；position-difference；error

1672-8262(2013)02-118-03

P228.43

A

2012—08—03

杨飞飞(1982—)，男，工程师，主要从事GPS技术应用研究。