一种基于无线传感器网络的分布式目标跟踪算法

孔 亮，孔令富，吴培良，付 磊

(1河北科技师范学院数学与信息科技学院，河北秦皇岛，066004;2燕山大学)

无线传感器网络(Wireless Sensor Networks，WSN)是由大量部署在监测区域的传感器节点组成，通过无线通信方式形成的一个多跳自组织网络系统，协作感知、采集和处理相关监测信息［1］。WSN的一项基本功能是对监测区域中的特定物理目标进行跟踪。由于WSN节点体积小，价格低廉，采用无线通信方式，以及网络部署随机，具有自组织性、鲁棒性和隐蔽性等特点，因此WSN非常适合于移动目标的跟踪［2～5］。从概率角度分析，基于WSN的移动目标跟踪问题即为根据WSN顺序接收到的特定观测量，连续地对目标位置进行估计的问题。其过程通常包括目标侦测、距离测算和目标定位3个主要阶段。目标侦测阶段，WSN节点可选择红外、超声、震动等技术根据侦测信号来判断移动目标是否出现。距离测算阶段，当WSN节点获得侦测信号后根据观测量估算其到移动目标之间的距离或方位信息。目标定位阶段，WSN节点利用获得的距离或方位信息互相协作，采用节点定位技术，确定移动目标的位置。由于目标跟踪系统常为非线性系统，本研究提出基于扩展卡尔曼滤波(Extended Kalman Filter，EKF)［6］的分布式跟踪算法。从仿真结果来分析，该算法达到很好的跟踪效果，十分适合于对精度和实时性要求较高的WSN中目标跟踪应用领域。

1 系统模型

1.1 运动模型

假设初始时刻移动目标出现在WSN监测区域的任意位置并遵循如下运动方程［7］移动，

其中，xt=(st，x，st，y)T表示t时刻移动目标的位置向量;vt=(vt，x，vt，y)T表示t时刻移动目标的速度向量;at=(at，x，at，y)T表示t时刻移动目标的加速度向量，服从高斯分布N(0，I);ΔT表示采样的时间间隔。记St=(st，x，st，y，vt，x，vt，y)T，可以将运动方程(1)和(2)改写为

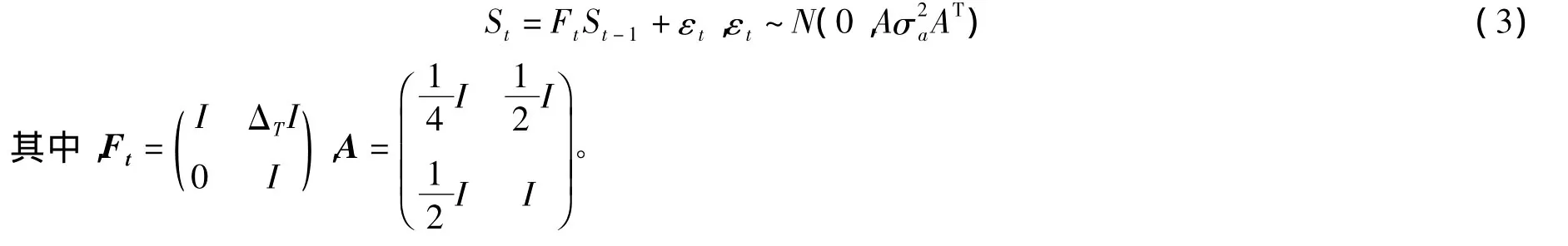
因此，目标的移动可由上述的线性高斯运动模型描述。

1.2 观测模型

Signal Strength Indicator，RSSI)［8］测距是WSN中应用较广的一种测距方法。它利用发射节点的发射信号强度、接收节点通过测量接收到的信号强度，根据已知的传播路径损耗模型估算出节点间的距离。本研究采用这种测量方式，观测量为无线传感器节点和移动目标之间的相对距离。假设t时刻节点i侦测到移动目标，则观测方程为

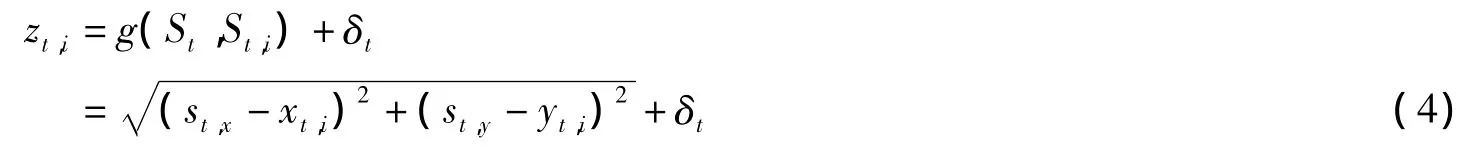
其中，St，i=(xt，i，yt，i)T表示无线传感器节点的位置向量;观测噪声 δt服从高斯分布N(0，)。

2 WSN下基于EKF的移动目标跟踪算法

基于WSN的目标跟踪问题，通常采用集中式方法，即将所有观测量发送到中心节点，而且整个数据处理过程也集中在中心节点上进行［5］。然而，由于WSN节点受能量等条件的制约，集中式通信和数据处理所产生的巨大能量消耗很可能会导致中心节点瘫痪［9］。为克服WSN集中式跟踪算法所存在的能量严重失衡的缺点，基于分布式的思想，根据移动目标的当前位置，将WSN节点动态组织成簇。假设移动目标周期性地发布无线电信号，WSN各节点最大通信范围相同且节点间已完成全局的时空统一。目标跟踪实现过程描述如下:

第1步，当移动目标进入WSN监测区域，根据无线传感器节点接收信号强度，选举距离移动目标最近的节点作为簇头节点。可同时与簇头节点和移动目标通信的节点被唤醒，成为该簇头节点的簇内节点。初始簇建立后，设定初始时刻(t=0)，当前簇头节点对移动目标状态进行初始化。

第2步，在采样时刻t，簇头节点作为簇的数据处理中心，接收并处理来自簇内各节点的观测量，形成移动目标位置的本地估计，同时WSN中簇外的节点进入休眠状态。

第3步，当休眠周期结束时，利用已知的全局坐标信息，以与移动目标预测位置最近为原则，选举新的簇头节点，根据第1步的方法组织新簇，同时若簇头节点发生变化，则通过打包通信将移动目标位置估计从原簇头节点发送到新的簇头节点。

第4步，上述动态分簇过程不断重复，直到目标脱离WSN监测区域。

在上述基于动态分簇的分布式目标跟踪过程中，WSN中各节点的能量消耗更加均衡，而且簇内节点的观测量均为有效观测，不存在冗余量，降低了数据处理的能量开销。由于本研究考虑的系统模型中运动模型是线性的，而观测模型是非线性的，因此各簇头节点使用EKF算法形成对移动目标位置的本地估计。假设已经得到t－1时刻移动目标的状态估计和误差协方差矩阵Pt－1|t－1，并且当前簇中的无线传感器节点集合为{1t，2t，…，mt}。根据EKF递推公式，t时刻移动目标定位算法描述为:

由运动方程(3)计算状态预测值和误差协方差矩阵Pt|t－1:

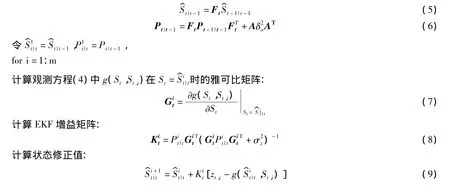
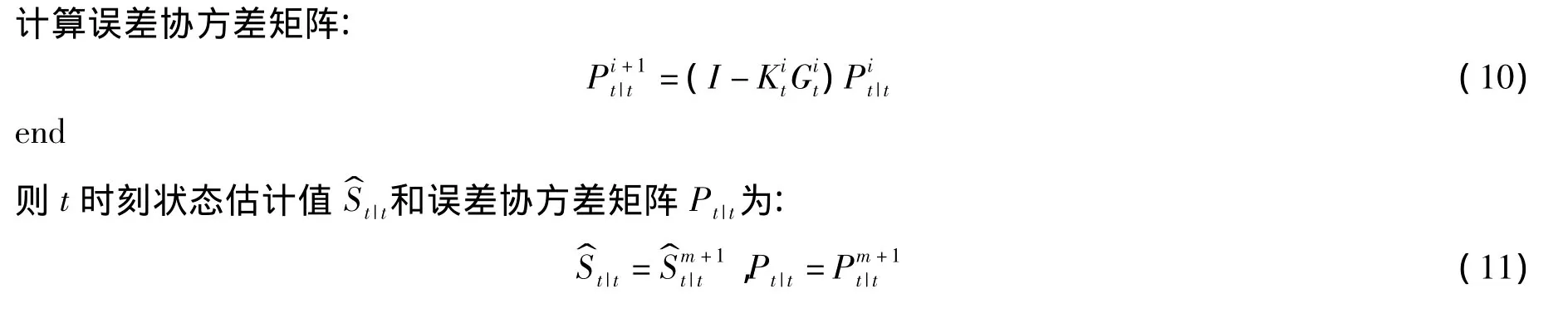
3 仿真分析

为验证本研究提出的基于WSN的分布式目标跟踪算法的性能，在MATLAB平台下与基于最小二乘和极大似然估计的跟踪算法进行对比仿真实验(以上3种算法分别简记为D-EKF，LS，MLE)。根据典型的WSN性能和目标运动特性，将仿真环境和初始条件设置如下:①WSN由100个节点组成，节点随机分布在1个50 m×50 m的区域中;②移动目标以大小0.2 m/s方向随机的初始速度随机出现在WSN监测区域中，加速度标准差σa=0.01;③RSSI测距模型中参考距离d0=1 m，参考信号强度P0=0 dBm，路径损耗因子np=2，噪声标准差σd=2;④WSN节点和移动目标的最大通信距离均为10 m;⑤观测噪声标准差σz=1;⑥WSN节点休眠周期与观测量采样时间间隔相同，均为ΔT=1 s。

设定D-EKF算法初始时刻移动目标位置向量为LS算法初始时刻状态估计值;MLE算法各时刻的初始迭代点为相同时刻LS算法的估计值。进行Nexp=20次独立仿真实验，每次实验采样100次，用3种算法对移动目标跟踪的均方根误差(Root Mean Square Error，RMSE)比较(图1，图2)，RMSE定义为

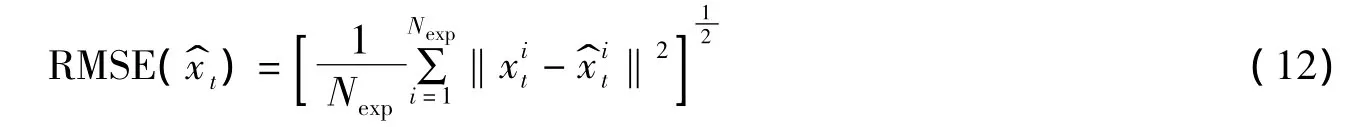
其中，和分别表示单次仿真实验中采样时刻t的移动目标位置真值和估计值。

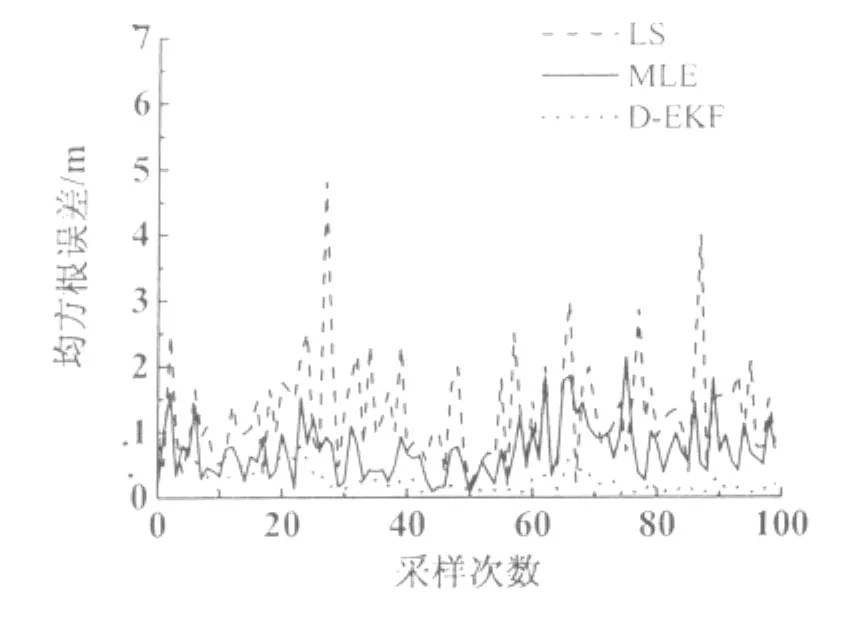
图1 x轴方向均方根误差对比

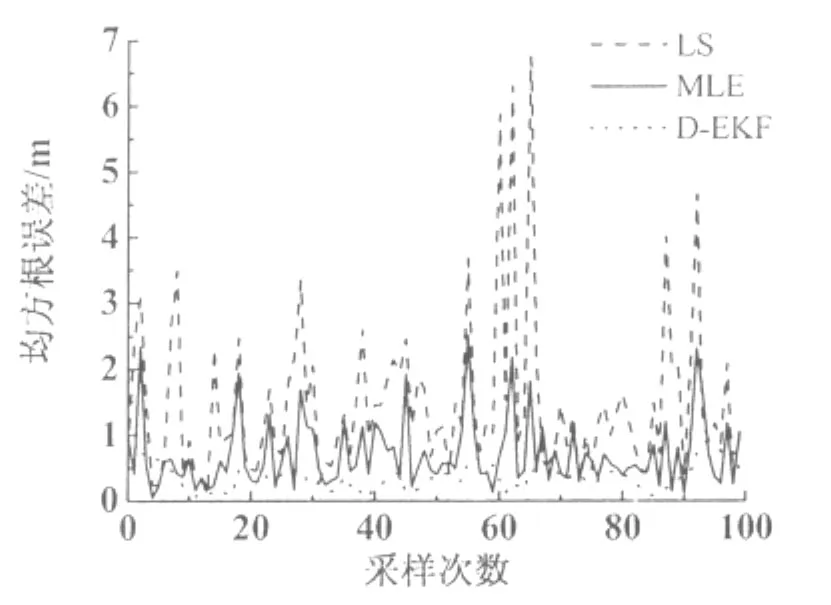
图2 y轴方向均方根误差对比

可以看出，与LS和MLE算法相比，本研究提出的D-EKF算法在移动目标跟踪精度方面有着明显的提高。若设置D-EKF算法初始时刻的移动目标位置为WSN监测区域中任意位置时进行20次独立仿真实验，其RMSE情况如图3图4所示。由图可以看出，由于EKF算法的自校正作用，D-EKF算法在移动目标跟踪过程中随着采样时刻的增加，不正确初值的影响会逐步消失，RMSE在采样时间轴上是收敛的。另外，从20次独立仿真实验中3种算法的平均运行时间和平均RMSE可以看出，虽然D-EKF算法与LS算法相比运算时间稍长，但是比MLE好很多(表1)。考虑到D-EKF算法的跟踪精度，本研究提出的D-EKF算法在移动目标跟踪中表现的综合性能要优于另外两种算法。

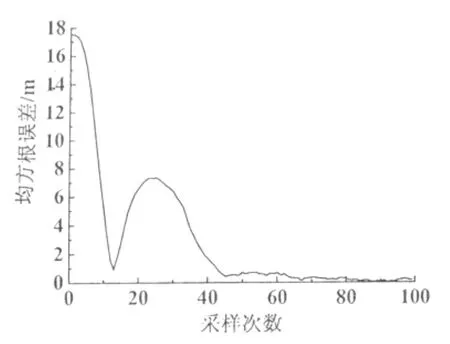
图3 x轴方向收敛情况

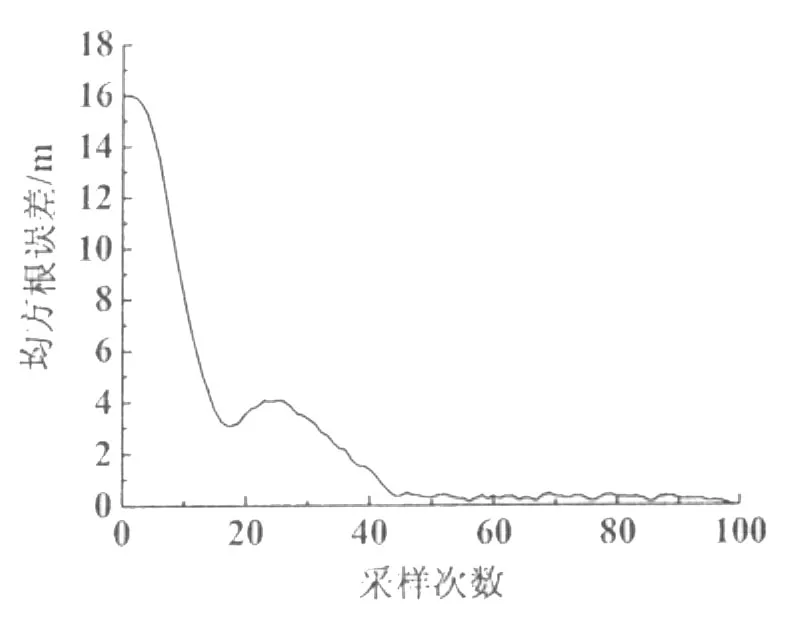
图4 y轴方向收敛情况

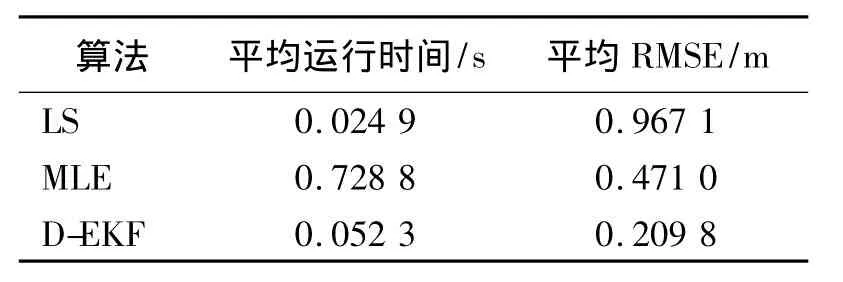
表1 3种算法的平均运行时间和平均RMSE对比

4 结 论

WSN是当前国际上前沿的新兴热点研究领域之一。由于其低成本、低功耗、高容错、自组织、多功能等特性，使得WSN在移动目标跟踪应用中具有传统网络无可比拟的优势。本研究提出的基于WSN的分布式跟踪算法，根据移动目标当前位置将WSN节点动态组织成簇，并以簇头节点作为数据处理中心，利用EKF形成对移动目标位置的本地估计。仿真结果表明，对比LS和MLE算法，本研究提出的基于EKF的分布式跟踪算法在精度、收敛性和实时性等方面达到很好的跟踪效果，十分适合于对精度和实时性要求较高的WSN中目标跟踪应用领域。

［1］ AKYILDIZ L，SU W，SANKARASUBRAMANIAM Y，et al.A survey on sensor network［J］.IEEE Communication Magazine，2002，8:102-114.

［2］ 彭远芳，黄晓峰.无线传感器网络目标跟踪算法的研究［J］.计算机仿真，2012，29(5):122-125.

［3］ 屈剑锋，柴毅，郭茂耘.无线传感器网络下的并行粒子滤波目标跟踪算法［J］.电子科技大学学报，2011，40(2):231-236.

［4］ 范乐昊，邱晓晖.分布式粒子滤波算法在面向跟踪的无线传感器网络中的应用［J］.南京邮电大学学报:自然科学版，2008，28(2):80-85.

［5］ 危阜胜，胥布工.基于无线传感器网络的分布式处理目标跟踪系统［J］.传感技术学报，2009，22(10):1 498-1 503.

［6］ 付梦印，邓志红，张继伟.Kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003.

［7］ B'EJAR B，BELANOVIC P，ZAZO S.Cooperative Localisation in Wireless Sensor Networks using Coalitional Game Theory［J］.Proceedings of the 18th European Signal Processing Conference，2010，6:1 459-1 463.

［8］ PATWARI N，ASH J N，KYPEROUNTAS S，et al.Locating the nodes cooperative localization in wireless sensor networks［J］.IEEE Signal Processing Magazine，2005，22(4):54-69.

［9］ KALANDROS M.Covariance control for multisensor systems［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38(4):1 138-1 157.

(责任编辑:石瑞珍)